Flux of Incoming Particles
Classically
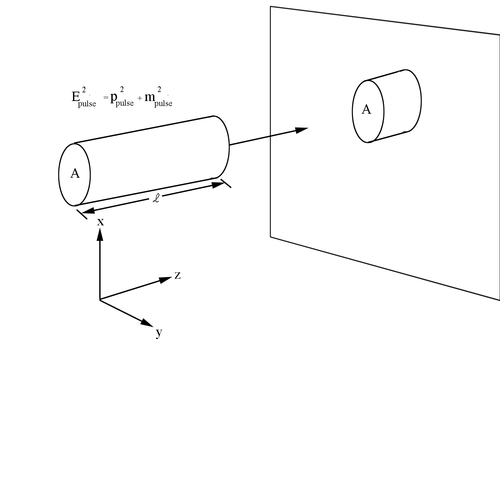
Working with a beam of electrons, we can define a pulse as n charges per unit volume, each carrying charge q and moving with speed [math]v_d[/math]. Defining [math]v_d[/math] to be the time-average speed of the electrons, we can find the number of particles within a beam. If A is the beam cross-sectional area, then l, the length of the pulse , has a volume Al with nAl charges within its bounds. Since each electron carries charge q, the total charge is
[math]Q\equiv nlqA [/math]
Defining the charge density as
[math]\rho \equiv \frac{Q}{V}=nlq\frac{A}{V}[/math]
The time it takes the pulse to move past a given point
[math] t=\frac{l}{v_d}[/math]
The total current is
[math]I=\frac{Q}{t}=\frac{nAlq}{\frac{l}{v_d}}=nAqv_d[/math]
The current density
[math]j\equiv \frac{I}{A}=nqv_d[/math]
[math]n=\frac{\vec j}{q\vec v_d}[/math]
where [math]\vec v_d[/math] is the drift velocity.
Beam Power =[math]\le 5000W\ (450A\ at\ 11GeV)[/math]
Relativistic Quantum Mechanics
[math]E^2 \equiv p^2+m^2[/math]
Using the operator relations
[math]\widehat{E}=i\hbar \frac{\partial}{\partial t} \qquad \widehat{ \vec{p}}=i\hbar \nabla[/math]
[math]\widehat{E}^2 \equiv \widehat{ \vec{p}}\ ^2+m^2\Rightarrow (i\hbar \frac{\partial}{\partial t})^2 \equiv (i\hbar \widehat{\vec{\nabla}})^2+m^2[/math]
Working with [math]\hbar=c=1[/math]
[math]\widehat{E}^2 \equiv \widehat{ \vec{p}}\ ^2+m^2\Rightarrow - \frac{\partial^2}{\partial t^2} \equiv (-\widehat{\vec{\nabla}})^2+m^2[/math]
Having this equation operate on a particle's wave function, we can obtain the relativistic Schrödinger equation, also known as the Klein-Gordon equation.
[math]-\frac{\partial^2 \phi}{\partial t^2}+\nabla^2 \phi=m^2 \phi[/math]
[math]\frac{\partial^2 \phi}{\partial t^2}-\nabla^2 \phi+m^2=0 [/math]
Letting [math]\Box \equiv \frac{\partial^2}{\partial t^2}-\nabla^2[/math]
The Klein-Gordon equation can be written as
[math](\Box+m^2)\phi =0[/math]
Multiplying by the complex conjugate
[math]\phi^*(\Box+m^2)\phi =0 \qquad \phi(\Box+m^2)\phi^* =0[/math]
Subtracting
[math]\phi^*(\Box+m^2)\phi - \phi(\Box+m^2)\phi^* =0[/math]
[math]\phi^*\Box \phi - \phi\Box \phi^* =0[/math]
[math]\phi^* (\frac{\partial^2}{\partial t^2}-\nabla^2) \phi - \phi( \frac{\partial^2}{\partial t^2}-\nabla^2) \phi^* =0[/math]
[math]\phi^* \frac{\partial^2}{\partial t^2} \phi-\phi^*\nabla^2 \phi - \phi \frac{\partial^2}{\partial t^2}\phi^*+\phi \nabla^2 \phi^* =0[/math]
[math](\phi^* \frac{\partial^2}{\partial t^2} \phi- \phi \frac{\partial^2}{\partial t^2}\phi^*)-(\phi^*\nabla^2 \phi -\phi \nabla^2 \phi^*) =0[/math]
[math]\frac{\partial}{\partial t} \underbrace{ \left [i \left (\phi^*\frac{\partial \phi}{\partial t}-\phi \frac{\partial \phi^*}{\partial t} \right ) \right ] }_{\rho}+\vec \nabla \cdot \underbrace{ \left [-i\left (\phi^*\vec \nabla \phi-\phi \vec \nabla \phi^* \right ) \right ] }_{\vec j}=0[/math]
From the conservation of probabilty, we know that
[math]-\frac{\partial}{\partial t}\int_V \rho dV=\int_S \vec{j} \cdot \hat{n} dS=\int_V \vec{\nabla} \cdot \vec{j} dV[/math]
[math]\frac{\partial \rho}{\partial t}=\vec{\nabla} \cdot \vec{j}=0[/math]
This can be written in the form
[math]\frac{\partial }{\partial t}\rho=\vec{\nabla} \cdot \vec{j}=0[/math]
where
[math]\phi=Ne^{i\vec p \cdot \vec x -iEt}[/math]
This gives
[math]\vec j=-i \left (\phi^* \nabla \phi -\phi \nabla \phi^* \right )[/math]
[math]\vec j=-i \left (Ne^{-i\vec p \cdot \vec x +iEt} \frac{\partial}{\partial z} Ne^{i\vec p \cdot \vec x -iEt}-Ne^{i\vec p \cdot \vec x -iEt}\frac{\partial}{\partial z}Ne^{-i\vec p \cdot \vec x +iEt} \right )[/math]
[math]\vec j=-i \left (Ne^{-i\vec p \cdot \vec x +iEt}i\vec p Ne^{i\vec p \cdot \vec x -iEt}+Ne^{i\vec p \cdot \vec x -iEt}i\vec pNe^{-i\vec p \cdot \vec x +iEt} \right )[/math]
[math]\vec j \equiv -i(2i\vec p)N^2=N^2 2p[/math]
and
[math]\rho=i \left (\phi^* \frac{\partial}{\partial t}\phi-\phi \frac{\partial }{\partial t}\phi^* \right )[/math]
[math]\rho=i \left (Ne^{-i\vec p \cdot \vec x +iEt} \frac{\partial}{\partial t}Ne^{i\vec p \cdot \vec x -iEt}-Ne^{i\vec p \cdot \vec x -iEt} \frac{\partial }{\partial t}Ne^{-i\vec p \cdot \vec x +iEt} \right )[/math]
[math]\rho=i \left (-Ne^{-i\vec p \cdot \vec x +iEt}iENe^{i\vec p \cdot \vec x -iEt}-Ne^{i\vec p \cdot \vec x -iEt} iENe^{-i\vec p \cdot \vec x +iEt} \right )[/math]
[math]\rho \equivi(-2iE)|N|^2=2E|N|^2[/math]
The number of particles in a beam passing through a unit area per unit time is
[math]\frac{Number\ of\ beam\ particles}{time\times Volume}=[/math]
[math]\frac{|\vec v_1|2E_1}{V}[/math]
The number of stationary target particles per unit volume is
[math]\frac{Number\ of\ target\ particles}{Volume}[/math]
[math]\frac{2E_2}{V}[/math]
Initial flux=[math]|\vec v_1|\frac{2E_1}{V} \frac{2E_2}{V}[/math]
[math]F=2E_1 2E_2|\vec {v}_1-\vec {v}_2|=4|E_1E_2\vec v_{21}|[/math]
where [math]v_{21}[/math] is the relative velocity between the particles in the frame where particle 1 is at rest
[math]\mathbf P_1 \cdot \mathbf P_2 = E_{1}E_{2}-(\vec p_1 \vec p_2)= E_{1}E_{2}[/math]
Using the relativistic definition of energy
[math]E^2 \equiv p^2+m^2=m^2[/math]
[math]\rightarrow \mathbf P_1 \cdot \mathbf P_2 =mE_{2}[/math]
Letting [math]E_{21}\equiv E_2[/math] be the energy of particle 2 wiith respect to particle 1, the relativistic energy equation can be rewritten such that
[math]|p_{21}^2| =E_{21}^2-m^2=\frac{(\mathbf P_1 \cdot \mathbf P_2)^2}{m^2}-m^2=\frac{(\mathbf P_1 \cdot \mathbf P_2)^2-m^4}{m^2}[/math]
where similarly [math]p_{21}[/math] is defined as the momentum of particle 2 with respect to particle 1.
The relative velocity can be expressed as
[math] v_{21}=\frac{|\vec p_{21}|}{E_{21}}[/math]
[math]F=2E_1 2E_2|\vec {v}_1-\vec {v}_2|=4|mE_{21}\vec v_{12}|=4|mE_{21}\frac{|\vec p_{21}|}{E_{21}}|=4m|\vec p_{21}|[/math]
The invariant form of F is
[math]F=4\sqrt{(\mathbf P_1 \cdot \mathbf P_2)^2-m^4}[/math]
[math]\mathbf P_1 \cdot \mathbf P_2 = E_{1}E_{2}-(\vec p_1 \vec p_2)[/math]
where in the center of mass frame [math]E_1=E_2[/math] and [math] \vec p_1^*=-\vec p_2^*[/math]
[math]\mathbf P_1 \cdot \mathbf P_2 = E_1^2+\vec p_1\,^{*2}[/math]
[math]F=4\sqrt{(E_1^2+\vec p_1\,^{*2})^2-m^4}=4\sqrt{(\vec p_1 \,^{*2}+m^2+\vec p_1\,^{*2})^2-m^4}[/math]
[math]F=4\sqrt{(2\vec p_1\,^{*2}+m^2)^2-m^4}=4\sqrt{4\vec p_1\,^{*4}+m^4+4\vec p_1\,^{*2}m-m^4}[/math]
[math]F_{cms}=4 \sqrt {4m^2\vec p_1\,^{*2}+4\vec p_1 \,^{*4}}[/math]
[math]F_{cms}=4 \sqrt {\vec p_1\,^{*2}4(m^2+\vec p_1 \,^{*2})}[/math]
As shown earlier
[math]s_{CM}=4(m^2+\vec p_1 \,^{*2})[/math]
[math]F_{cms}=4 \sqrt {\vec p_1^*\,^2s}[/math]
