Trash

12-12-08

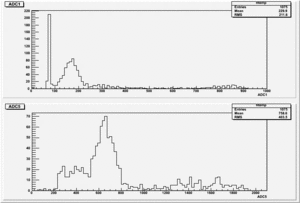
Finding out what is gain for each channel using the Stanford pulse generator.

Setting:

Run Number: r634 && r635

Original pulse from stanford pulse generator goes to the ADC: r636 && r637

I used the attenuator for both channels and it was set to the same value: 12dB = 10.7918.

[math]X db = 20 log_{10}\frac{I_1}{I_2}[/math]

[math]\frac{I_1}{I_2} = 10^{12/20} = 3.98[/math]

Gain Calculation

Gain_for_Channel_1 = Gain_TrigOut = [math]\frac{175 \times 10.7918}{110} = 17.1688[/math]
Gain_for_Channel_5 = Gain_Strip = [math]\frac{650 \times 10.7918}{145} = 48.377[/math]

TrigOut and the stripsignal, both are used as a pulse and go to ADC.
The pulse from the Strips is used as a trigger and gate.

The pulse from the trigout is delayed, Amplified by the Timinig Filter Amplifier(Coarse_Gain=X20, Fine_Gain=8.5 && Integrate=20ns).
Signal from the Strips goes to the Timing Filter Amplifier(Coarse_Gain=X20, Fine_Gain=10.5 && Integrate=20ns). Amplified pulse is devided into two signals, One is sued as a trigger and gate and second as a pulse for ADC. The first one(gate && trigger) is amplified using the Timing Filter Amplifier(Coarse_Gain=X2, Fine_Gain=10 && Integrate=50ns) and used in DIFF. CFD for gate and trigger. Second output from the Amplified strips, goes to delay box(TENNELEC TC 215 DELAY AMPLIFIER) and putted to the ADC.

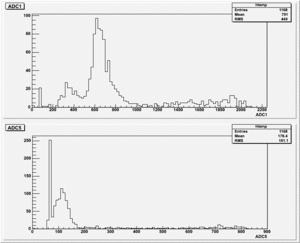
The results shown below are for different Diff. CFD values.

1). Threshold Values: Threshold=1.90, ULD=9.65 && LLD=2.10

Run Number is r613

Start time: Dec 11 16:31:42 End Time: Dec 11 17:32:23

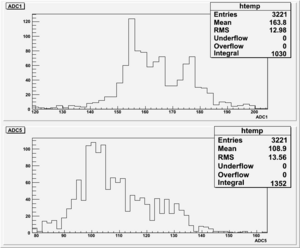
2). Threshold Values: Threshold=3.10, ULD=9.65 && LLD=2.90

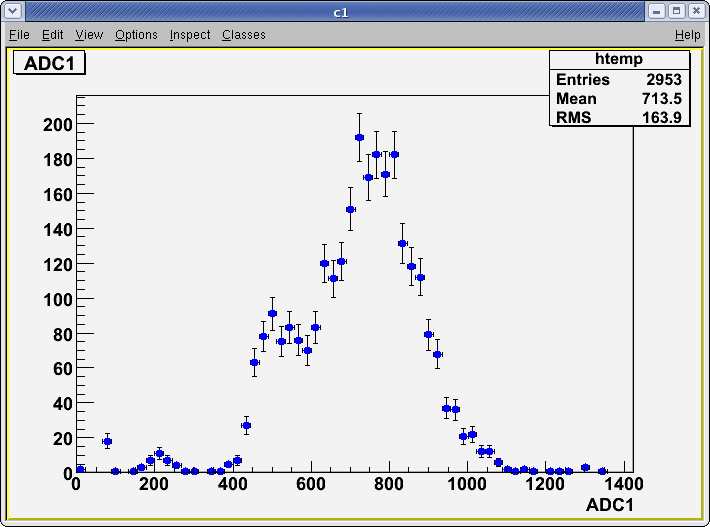
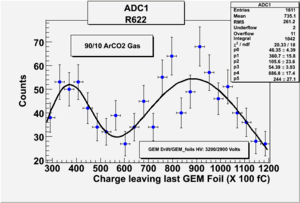
Run Number is r622

Start time: Dec 11 19:25:28 End Time: Dec 11 21:53:44

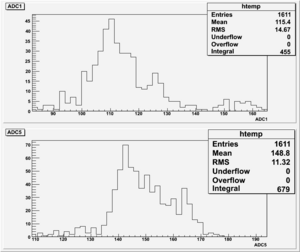
2). Threshold Values: Threshold=3.70, ULD=9.65 && LLD=3.50

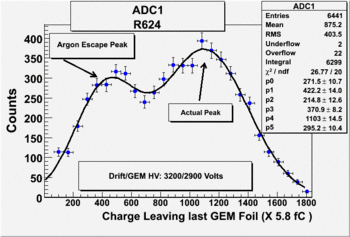
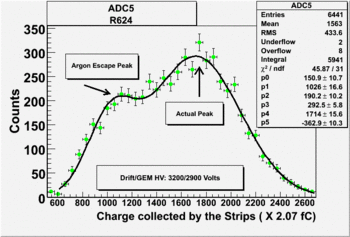
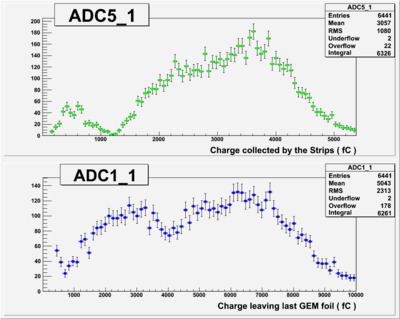
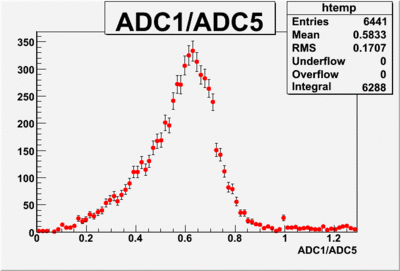
Run Number is r624

Start time: Dec 11 21:58:37 End Time: Dec 12 12:19:53

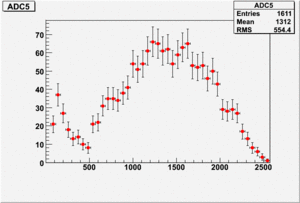
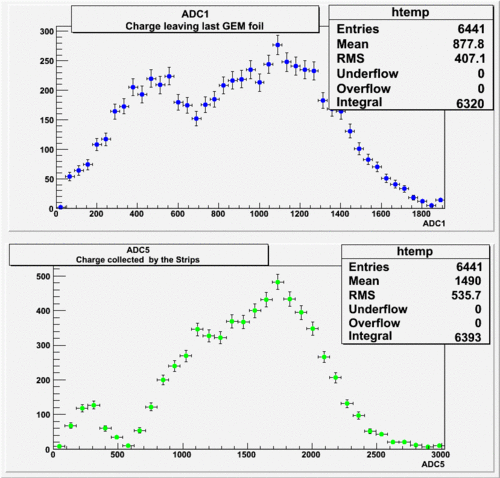
The result shown below is reasonable. The charge that left the last GEM foil is greater than the charge collected by the strips.

QCD and asymptotic freedom

In non-Abelian gauge theories, the beta function can be negative, as first found by Frank Wilczek, David Politzer and David Gross. An example of this is the beta-function for Quantum Chromodynamics (QCD), and as a result the QCD coupling decreases at high energies.

Furthermore, the coupling decreases logarithmically, a phenomenon known as asymptotic freedom. The coupling decreases approximately as

[math] \alpha_s(k^2) \ \stackrel{\mathrm{def}}{=}\ \frac{g_s^2(k^2)}{4\pi} \approx \frac1{\beta_0\ln(k^2/\Lambda^2)}[/math]

where β₀ is a constant computed by Wilczek, Gross and Politzer.

Conversely, the coupling increases with decreasing energy. This means that the coupling becomes large at low energies, and one can no longer rely on Perturbation theory.

[1]

Thesis

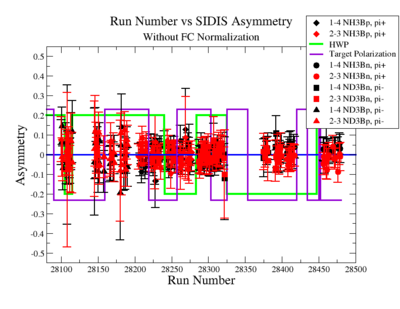
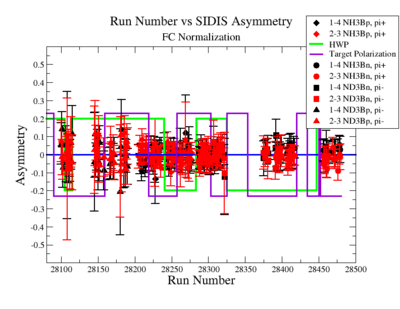
The SIDIS asymmetries for each target type, hadron type and run number ([math]\pi^{+}[/math] and [math]\pi^{-}[/math]) are shown on Fig. 2.17 before and after FC normalization:

Figure 2.17. Run Number vs Semi inclusive asymmetry before and after FC Normalization.

unless the runs can be combined to show sign changes like in figure 2.16, this plot may not be too useful given the table below
You might try doing the above plot with only the pi+ asymmetries

The electron asymmetries for each target type, before and after FC normalization are listed in Table 4.2.

Run Group	Target Type	Before FC	After FC
ND3	[math]A_{1-4}[/math]	[math](0.12 \pm 0.77) %[/math]	[math](0.11 \pm 0.79) %[/math]
	[math]A_{2-3}[/math]	[math](-0.06 \pm 0.78) %[/math]	[math](-0.09 \pm 0.81) %[/math]
NH3	[math]A_{1-4}[/math]	[math](0.61 \pm 0.71) %[/math]	[math](0.72 \pm 0.72) %[/math]
	[math]A_{2-3}[/math]	[math](-0.78 \pm 0.71) %[/math]	[math](-0.73 \pm 0.71) %[/math]

Table 4.2. Electron Asymmetries for NH3 and ND3 targets before and after FC Normalization .

Maybe I don't understand the above table, but Figure 2.16 clearly shows non-zero asymmetries while the uncertainties in the above table indicate that everything is zero.

User_talk:Tamar