HRRL 03-17-2011
Accelerator Tuning
Good Tune Used for good Scan
By Dr. Kim
Scan Description
This is scan for 14 MeV beam. 40 mAmps peak current. Q1 is on, All other quads are off.
1) Scan from -5 Amps to 5 Amps
2) Increment at 0.2 Amps.
3) Name images by numbers start from 1. Then go on.
Like: -5 Amp is 1, -4.8 Amp is 2, and so on til 5 Amp is named 51.
4) Scan multipole times from -5 to 5 Amps, and put them in different folders.
5) For each time, take back ground images. It should be done when RF is on and gun is off.
6) After the scan take a scope image for the current of the FC after the OTR screen.
Calibration
| image | OTR image | cal_h (mm/px) | cal_v (mm/px) |
 |
 |
0.04308 | 0.04204 |
 |
 |
0.04320 | 0.04228 |
 |
 |
0.04349 | 0.04181 |
 |
 |
0.04323 | 0.04196 |
 |
 |
0.04337 | 0.04212 |
| mean (mm/px) | mean (mm/px) | ||
Results
Q1
At lower current background subtraction gets worse, because singal/noise drops.
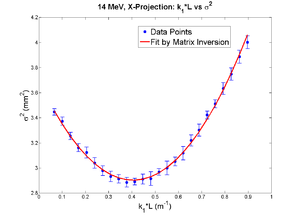
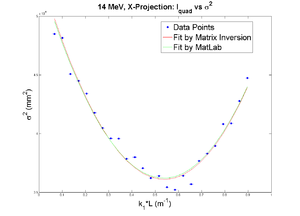
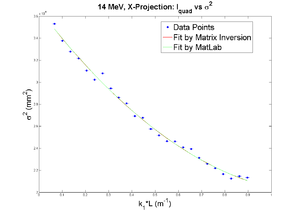
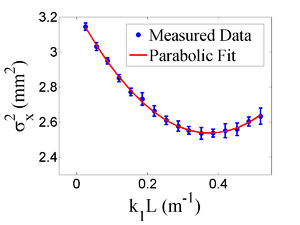
42 mA, Positive Current, X projection
emit=0.388 +- 0.008 mm*mrad, emit_norm=10.64 +- 0.22 mm*mrad
beta=1.285 +- 0.024, alpha=0.94 +-0.03
//K1*L(1/m) er K1*L sgima^2(mm) er sigma^2
Media:2011_Mar_Emit_fit_data_x.txt
parabola fit for x-projection:
parabola fit for y-projection (y in mm unit):
y = (3.69167 +-0.02346) + (-3.89000+-0.12250)*x + (4.79738+-0.13309)*x.*x
Data created from parabola fit
Media:2011_Mar_Emit_data_from_fit_x.txt
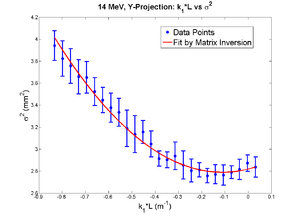
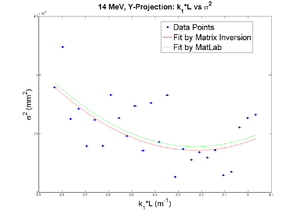
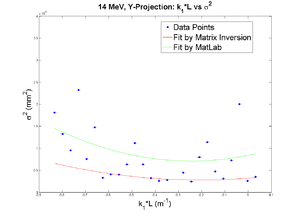
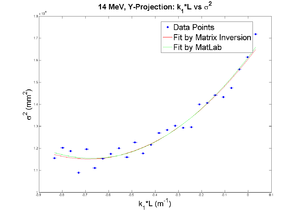
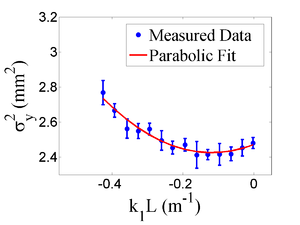
42 mA, Negative Current, Y projection
emit=0.266 +- 0.018 mm*mrad, emit_norm=7.30 +- 0.50 mm*mrad
beta=0.918 +- 0.068, alpha=0.19 +-0.06
//K1*L(1/m) er K1*L sgima^2(mm) er sigma^2
Media:2011_Mar_Emit_fit_data_y.txt
parabola fit for y-projection (y in mm unit):
y = (2.81806 +-0.03890) + (0.52202+-0.26284)*x + (2.35025+-0.34553)*x.*x
Data created from parabola fit
Media:2011_Mar_Emit_data_from_fit_y.txt
X and Y emittances are different. The parabola in X reaches min around 0.4, while in Y reaches around 0.15. Which suggests quadrupole strengths of X and Y are way different for same coil current. Which might suggest beam is not centered, because when beam is off-centered we have this can occur.
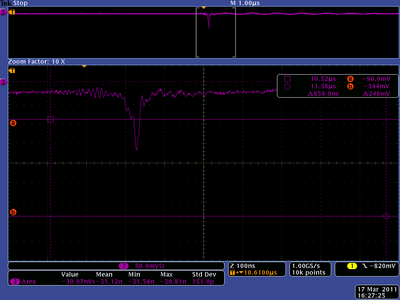
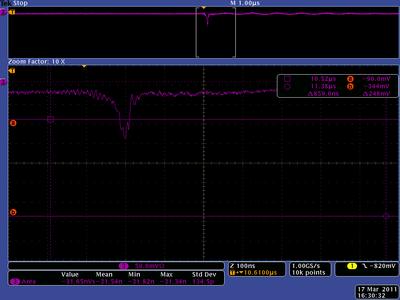
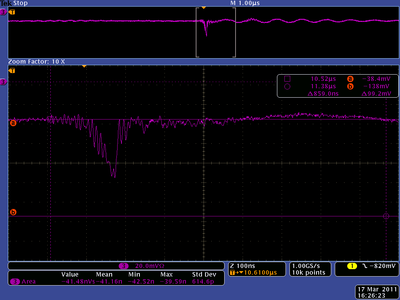
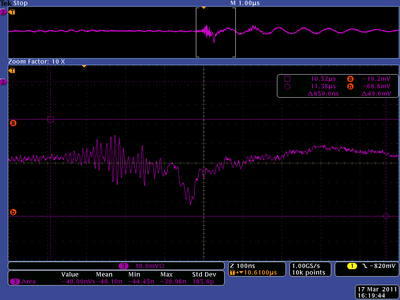
20 mA, Positive Current, X projection
10 mA, Positive Current, X projection
5 mA, Positive Current, X projection
Q4
42 mA All Other Quads off
Haven't reach minimum.
42 mA Q1_at_-2A, Q2_at_+8A, Q3_at_-6A
x-projection:
y-projection:
Fits After the Second Mapping of the Quad
I mapped the quad to find effective length of the quad for different currents. Results are at: Second Mapping of Quadruple Magnets
MATLAB Scripts
Media:hrrl_2011_marc_emit_test_marc17_SuperGaussian_Fit.txt
Media:hrrl_2011_marc_emit_test_marc17_SupGau_devsum.txt
Media:hrrl_2011_marc_emit_test_marc17_Emit_Parabola_Fit_kl_XProjection.txt
Media:hrrl_2011_marc_emit_test_marc17_Emit_Parabola_Fit_kl_YProjection.txt
Media:hrrl_2011_marc_emit_test_marc17_Trial_my_superGaussian_Fit.txt
Media:hrrl_2011_marc_emit_test_marc17_Plot_Beam_Spot.txt
Media:hrrl_2011_marc_emit_test_marc17_Three_d_surface_plotter.txt
Media:hrrl_2011_marc_emit_test_marc17_my_superGaussian_Fit.txt
Media:hrrl_2011_marc_emit_test_marc17_devsum.txt
Media:hrrl_2011_marc_emit_test_marc17_countor_plotter.txt
With thin lens approximation method
Why y projection has bigger error?
For data look at here: HRRL-03-17-2011-fit-error-ana From the data we can see that sigma (rms) of Y-projection are more spread, ie. has bigger standard deviation, than the of X-projection.
I think this is due to the beam profile in Y-projection contains less pixels than X- projection. (This is due to Y-projection observed with 45 degree angle, so Y-profile got squeezed).
So, Y-projection has less data for fitting, thus this creates bigger standard deviation for sigma (rms) value of the Y-projection.
Quad was mapping for the second time to find effective length for the different currents. Link is at [[1]].
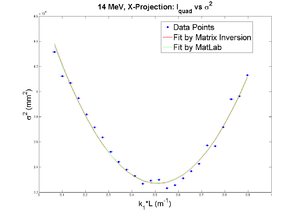
X
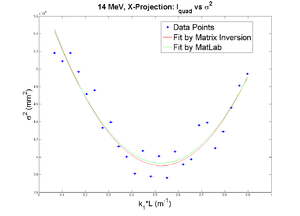
x-projection:
emit=0.369 +- 0.019 mm*mrad, emit_norm=10.10 +- 0.51 mm*mrad
beta=1.40 +- 0.06 m, alpha=0.97 +- 0.06 rad
parabola fit for y-projection (y in mm unit):
y = (3.23007 +-0.01742) + (-3.70339+-0.17170)*x + (4.94449+-0.33370)*x.*x
Y
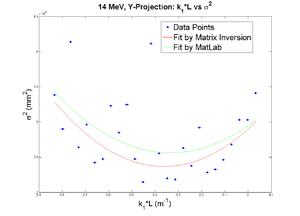
y-projection:
emit=0.294 +- 0.038 mm*mrad, emit_norm=8.06 +- 1.05 mm*mrad
beta=1.17 +- 0.13 m, alpha=0.24 +- 0.07 rad
parabola fit for y-projection (y in mm unit):
y = (2.47210 +-0.02580) + (0.78376+-0.30261)*x +(3.29515+-0.73747)*x.*x
Energy Measurement
Energy Current (MeV) (mA) 14.6469 0.6 14.8240 1.2 14.9985 3.2 15.1704 3.0 15.3398 2.4 15.5066 1.3 15.8325 0.4
Here used dipole mapping Kiwi_Dipole_Mappings#Estimation_for_En_vs_I
Amplitude = 3.23464, mean = 15.14254, sigma = 0.26190
Gaussian Fit for Electron Beam Energy: En = 3.23464exp(-(En-15.14254)^2) / (2*0.26190^2)
Gaussian Energy peak = 15.14254
Energy spread = 1.57142 rms Energy spread = 0.26190
Relative Energy spread = 0.10378 Relative rms Energy spread = 0.01730