Faraday Cup Analysis

Go Back

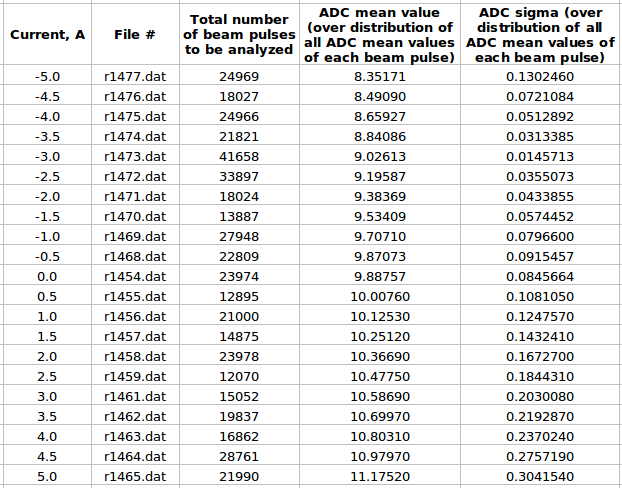
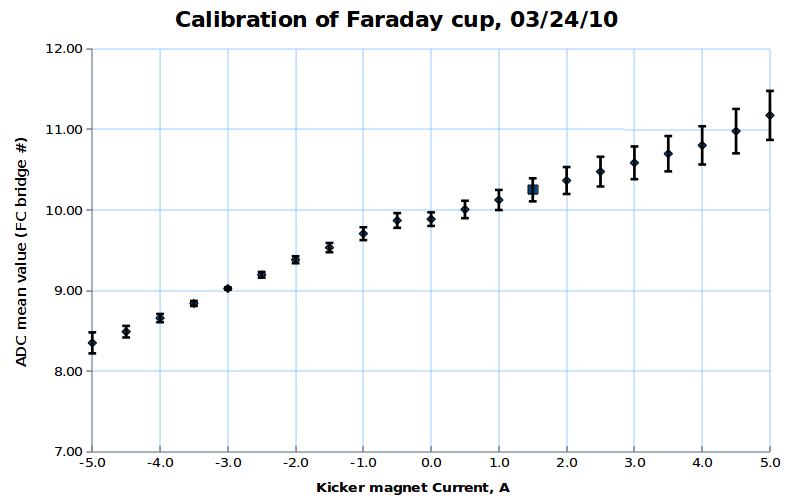
Kicker magnet calibration

by using pulse by pulse ADC channel mean value distribution

\gamma\gamma For each beam pulse:

[math] X^{pulse}_{avg}=\frac{\sum_{i=1}^{16}{Q_{i}*i}}{\sum_{i=1}^{16}{Q_{i}}}[/math] (average beam position for one pulse)

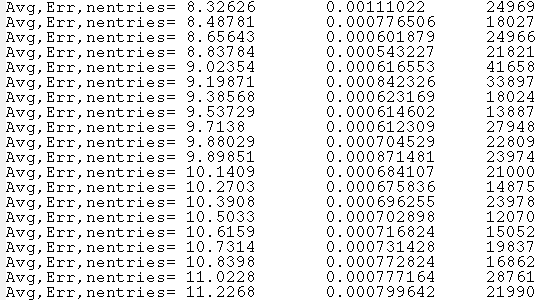
For distribution over all beam pulses:

[math] X_{avg}=\frac{\sum_{i=1}^{pulses}{X_{avg}^{pulse}}}{pulses}[/math] (average beam position over all pulses)

[math] X_{err}={\sqrt{\frac{1}{pulses}\sum_{i=1}^{pulses}{\left(X^{pulse}_{avg}-X_{avg}\right)^{2}}}}[/math] (absolute error)

Here is:
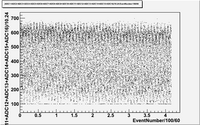
1. ADC# = bridge#
2. Pulse# = ReadOut# = Entry# = Event#

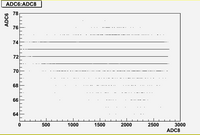
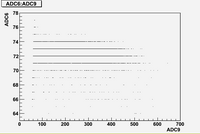
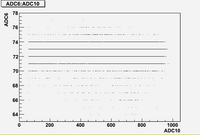
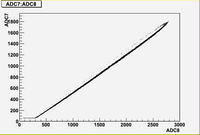
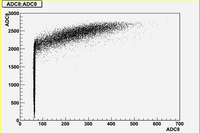
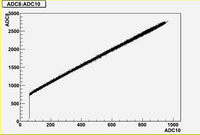
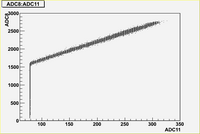
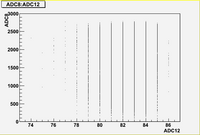
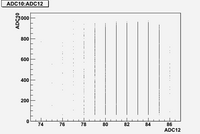
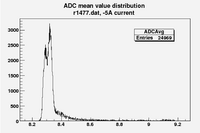
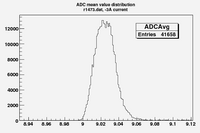
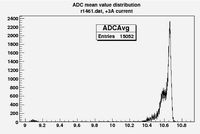
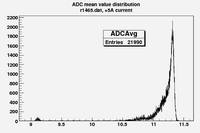
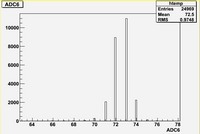
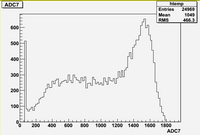
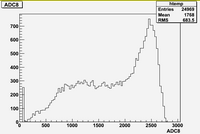
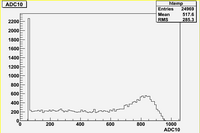
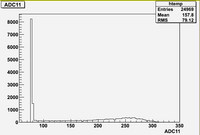
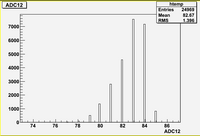
Some examples of ADC mean value distribution. Here are:
1. x axis: ADC mean value for one pulse
2. y axis: number of pulse w/ that ADC mean value

by using ADC channel charge distribution

For each ADC channel:

[math] Q_{channel}=\sum_{i=1}^{pulses}{Q^{pulse}_{channel}}[/math]     (total charge per one ADC channel)

[math] q_{channel}=\sum_{i=1}^{pulses}{\sqrt{Q^{pulse}_{channel}}}[/math]     (absolute error in charge distribution per one ADC channel assuming Poisson)

For each ADC channel we have  (Q +- q)

For distribution over all ADC channel:

[math] X_{avg}=\frac{\sum_{i=1}^{16}{iQ_{i}}}{\sum_{i=1}^{16}{Q_{i}}}[/math]     (average beam position over all pulses)

[math] X^2_{err}=\frac{\sum_{i=1}^{16}{i^2q^2_{i}}}{\sum_{i=1}^{16}{Q^2_{i}}}+\frac{(\sum_{i=1}^{16}{iQ_{i}})^2\sum_{i=1}^{16}{q^2_{i}}}{\sum_{i=1}^{16}{Q^4_{i}}}[/math]     (absolute error)

For all ADC channel we have [math]ADC_{avg}[/math]+-[math]ADC_{err}[/math]

Here are results:

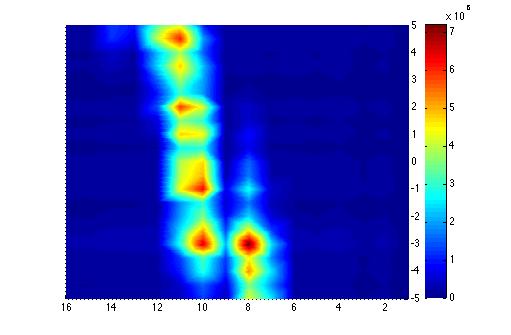
Faraday Cup 3D plot

Below is the plot of the charge in Faraday cup (pC) as a function of magnet current (vertical axis, A) (basically magnetic field) and ADC (horizontal axis).

What about moving beam? splitting beam?

in time charge distribution plots (Run 1477 -5A)

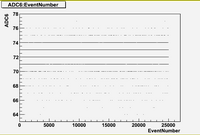
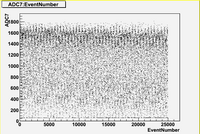
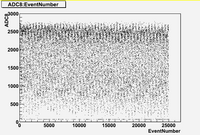
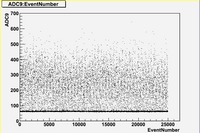
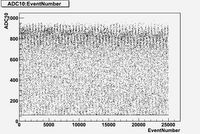
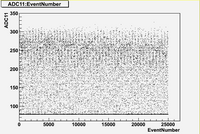
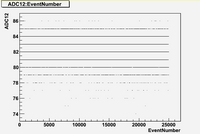
As we can see from plots above:
1. There are no beam on blocks 6 and 12.
2. There are beam on blocks (7, 8, 9, 10)
3. The total charge for blocks (7, 8, 9, 10, 11) is strongly fluctuates with time.

Also it is interesting to note the switching in mean value of charge distribution from "up" (blocks 7,8) to "down" (blocks (9,10,11)
This switching in mean value position is easy to see if we plot the histogram of charge distribution.

Question:
1. Is it moving beam?
2. Or is it maybe splitting of beam into two beams with very unstable current fluctuation?

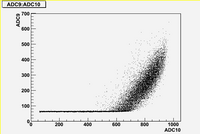
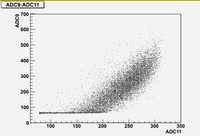
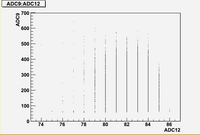
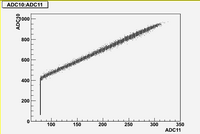
correlation plots (Run 1477 -5A)

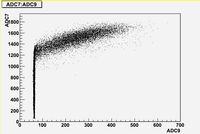
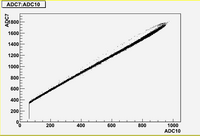
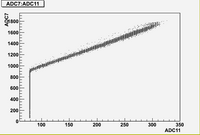
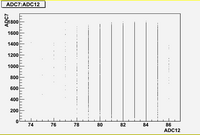
As we can see from plots above, there are strong correlations between blocks (7, 8, 10, 11)
There are weak correlation between blocks (9) and (7, 8, 10, 11)
And there are no correlation between blocks (6, 12) and all other blocks.

For moving beam I would expect the negative correlation between blocks (7, 8, 9, 10), if somewhere decrease, somewhere increase
So because the positive correlation between blocks (7, 8, 10, 11)
we have beam splitting into two beams with very unstable current?

This structure can be seen if I plot histogram for charge distribution for all ADC blocks

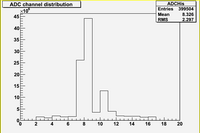
Here is interesting to note that the total charge for first peak (blocks 7, 8) is about 3 times more then for second peak (blocks 10, 11)
It would be interesting to see this ratio for all other kicker magnet current values. Is it constant?
Also it would be interesting to see the structure of the splitting for different current values.
Let see how it looks

Error Analysis

The ADC measures the charge deposited on each of the 16 Aluminum blocks. The ADC is a 12 bit ADC with a max input of 400 pc. THe means that the charge per channel is:

[math]\frac{400 \mbox{pC}}{2^{12}\mbox{Channels}} = \frac{400 \mbox{pC}}{4096\mbox{Channels}} =\frac{1 \mbox{pC}}{10.24 \mbox{Channels}} [/math]

Run1477 -5A

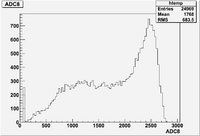
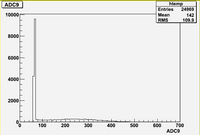
Raw ADC result for channel 8 :

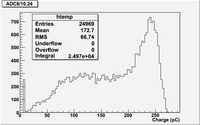
ADC 8 using channel -> Coul conversion:

The above histogram shows an RMS of 66.74 pC.

Comment

The ADC basically counts the number of electrons collected by the aluminum FC bricks and transfered through the cables to the ADC. This is a poisson process with a large number of trials leading to a large mean value [math](\mu)[/math]. One would expect a gaussian parent population with

[math]\sigma = \sqrt{\mu}[/math]

The histogram shows

Mean = [math]172.7 =\frac{\sum_i^N x_i}{N}[/math]

RMS = [math]66.74 = \frac{\sqrt{\sum_i^N(x_i - 172.7)^2}}{N}[/math]

[math] \sqrt{172.7} = 13.1 \ll 66.74[/math]

What does this mean?

The theoretical distribution would be Guassian with [math]\sigma = \sqrt{\mu}[/math]. The above suggests that the beam charge delivered to the FC is not following this statistical parent distribution. Most likely the beam current is changing while you are measuring the charge with the FC.

Is the charge lost or is it just moving to different FC channels

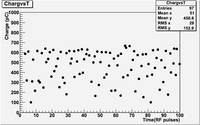
Within 100 RF pulses the total charge on the FC drops from 600 to 100 pC. It seems the beam current is very unstable.

There also appears to be a gaussian distribution centered around 600 pC and a wider one centered around 100 pC.

Could it be that I can put a cut on total beam current and see if the charge moves between FC elements?

Let see what the total charge looks like for 3 cases.

Go Up Go Back