[math]\textbf{Navigation}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]
A bash script to run the GEMC simulations is created. tcsh scripts to run root2evio on lds2 is called using sshpass. The lds2 scripts use sshfs
The main script on lds3:
BUILD_GEMC_SIMULATION.sh
The 3 scripts on lds2:
first_commands.tcsh
second_commands.tcsh
last_commands.tcsh
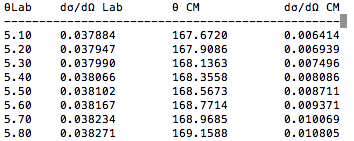
LUND File Output
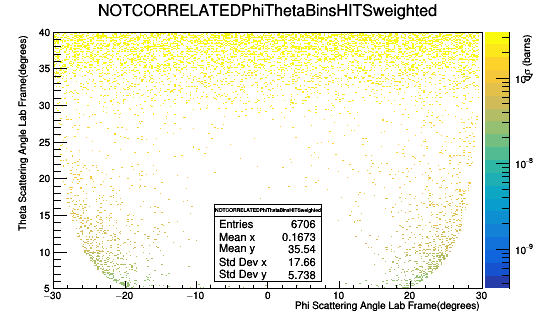
0.1 degree spacing in the Lab frame. CM Frame is not evenly spaced.
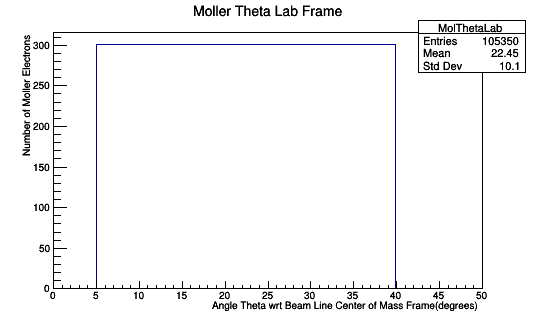
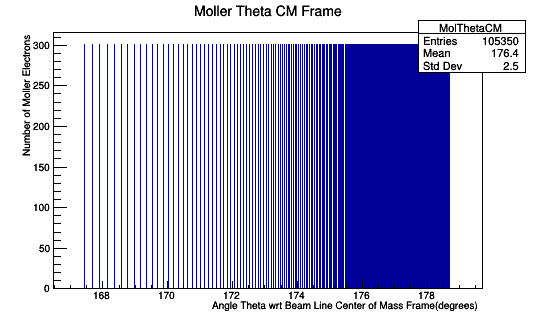
Applying the weight
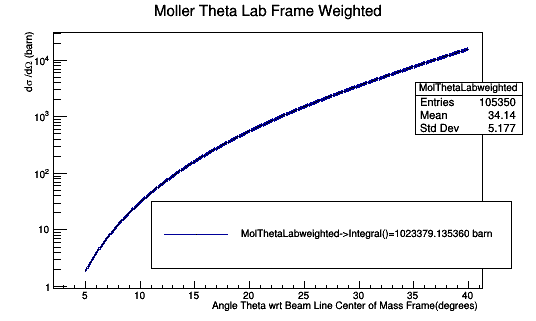
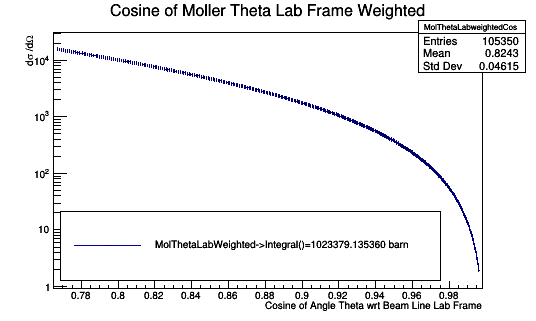
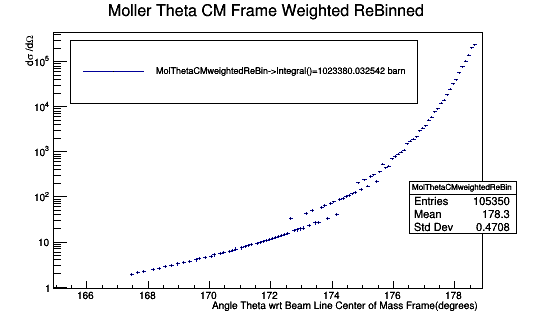
Looking at the angles and the associated weight, we can find the sums
Once_Angles_and_weight=3399.930890560805437
Total_Angles_and_weight=1023379.198058736044914
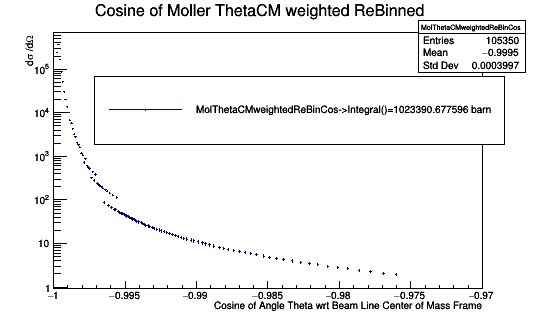
Checking with Mathematica
"Integrating" with Cosine term
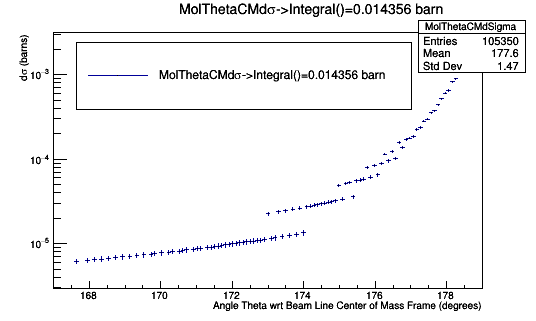
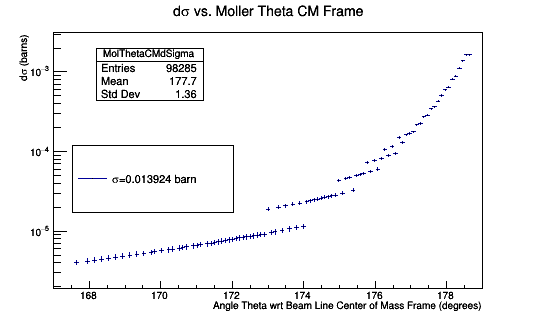
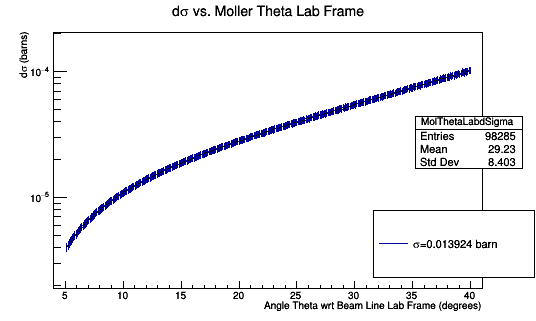
Finding the Cross Section
Performing a Riemann sum for [math]-30^{\circ} \lt \phi \lt 30^{\circ}[/math]
The cross section should be equal between both frames since the number of particles is an invariant. The differential cross section must differ between frames since the solid angle does vary.
[math]\sigma_{(CM)}=\sigma{(Lab)}[/math]
[math]\frac{d\sigma}{d\Omega}_{(CM)} d\Omega_{(CM)}=\frac{d\sigma}{d\Omega}_{(Lab)} d\Omega_{(Lab)}[/math]
[math]\frac{d\sigma}{d\Omega}_{(CM)} \sin \theta_{(CM)}\ d\theta_{(CM)}\ d\phi=\frac{d\sigma}{d\Omega}_{(Lab)} \sin \theta_{(Lab)}\ d\theta_{(Lab)}\ d\phi[/math]
[math]\rightarrow \frac{d\sigma}{d\Omega}_{(Lab)}=\frac{d\sigma}{d\Omega}_{(CM)} \frac{\sin \theta_{(CM)}\ d\theta_{(CM)}\ d\phi}{ \sin \theta_{(Lab)}\ d\theta_{(Lab)}\ d\phi}[/math]
[math]\rightarrow d\sigma_{(Lab)}=\frac{d\sigma}{d\Omega}_{(CM)} \frac{\sin \theta_{(CM)}\ d\theta_{(CM)}\ d\phi}{ \sin \theta_{(Lab)}\ d\theta_{(Lab)}\ d\phi}\sin \theta_{(Lab)} d\theta_{(Lab)}\ d\phi[/math]
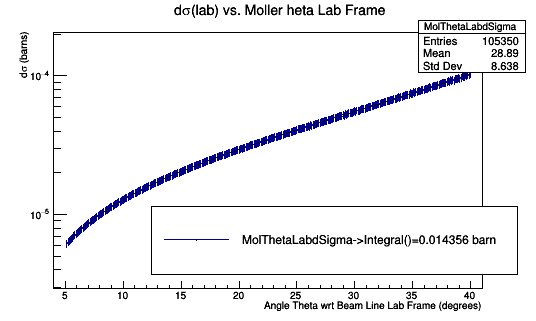
Adjust for DC Sector 1 Limits
GEMC Cross Section
Only taking GEMC hits in Sector 1 with Track ID of the mother of the FP equal to zero:
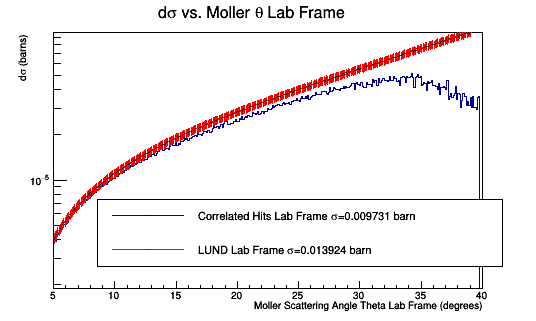[math]\frac{0.009731\ barn}{0.013924\ barn}=70\%[/math]Efficiency
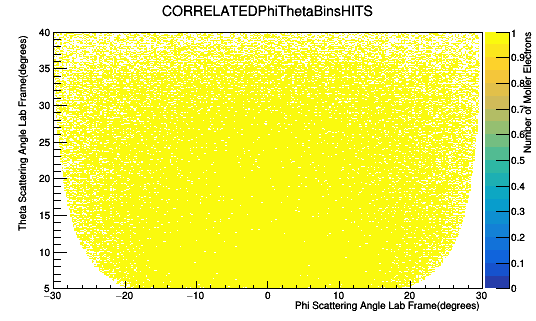
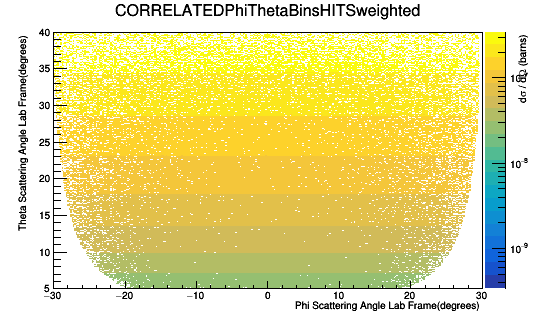
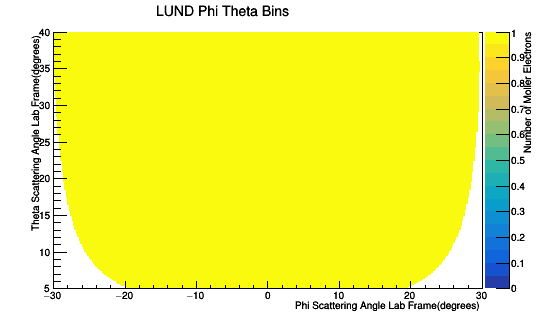
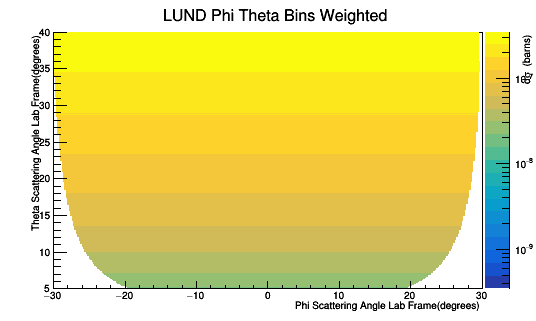
Taking GEMC hits with ANY Track ID of the mother of the FP :
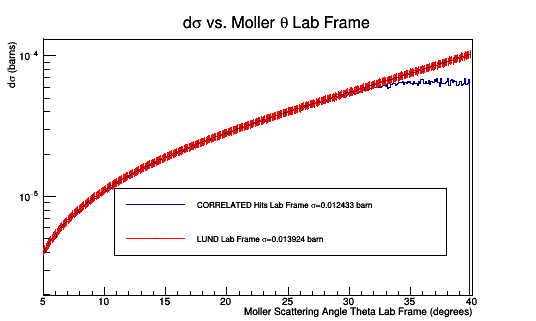[math]\frac{0.012433\ barn}{0.013924\ barn}=90\%[/math]Efficiency
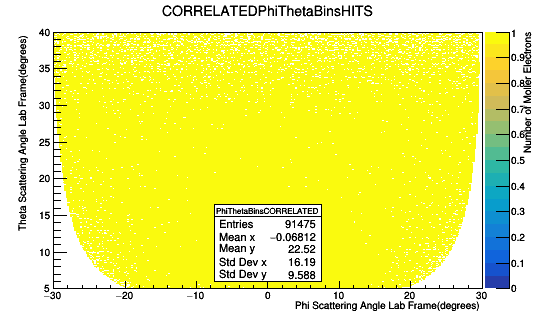
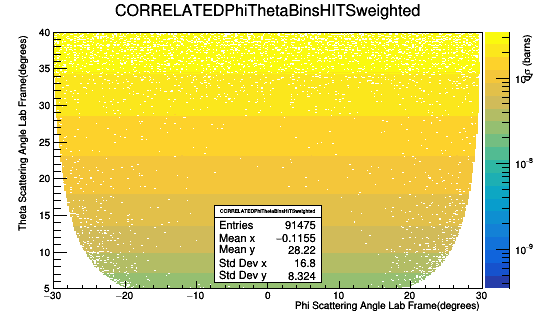
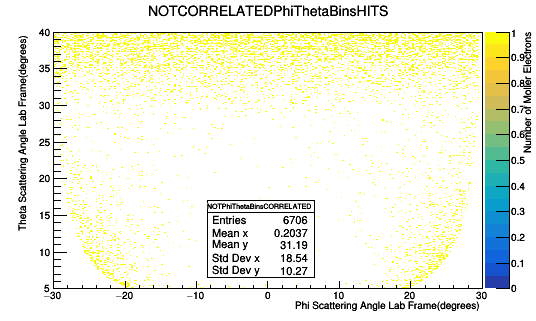
Using the Cross Section
[math]\sigma \equiv \frac{N_{scattered}}{\mathcal{L}t}=\frac{N_{scattered}}{N_{incident}\rho \ell }[/math]
Occupancy
LH2_NOSol_0Tor_11GeV_IsotropicPhi_v2_6_ShieldOut
Run
./BUILD_GEMC_SIMULATION.sh
DVMacro
Clas12Mon
Create hipo file
Move hipo file to clas12mon folder
mv LH2_NOSol_0Tor_11GeV_IsotropicPhi_v2_6_ShieldOut.hipo ~/clas12mon
Run monitor program
./README
Load hipo file
"Press H for hipo"
"Press play"
"Switch to
For [math]5^{\circ}\gt \theta\lt 40^{\circ}\ -30^{\circ}\gt \phi\lt 30^{\circ}[/math]
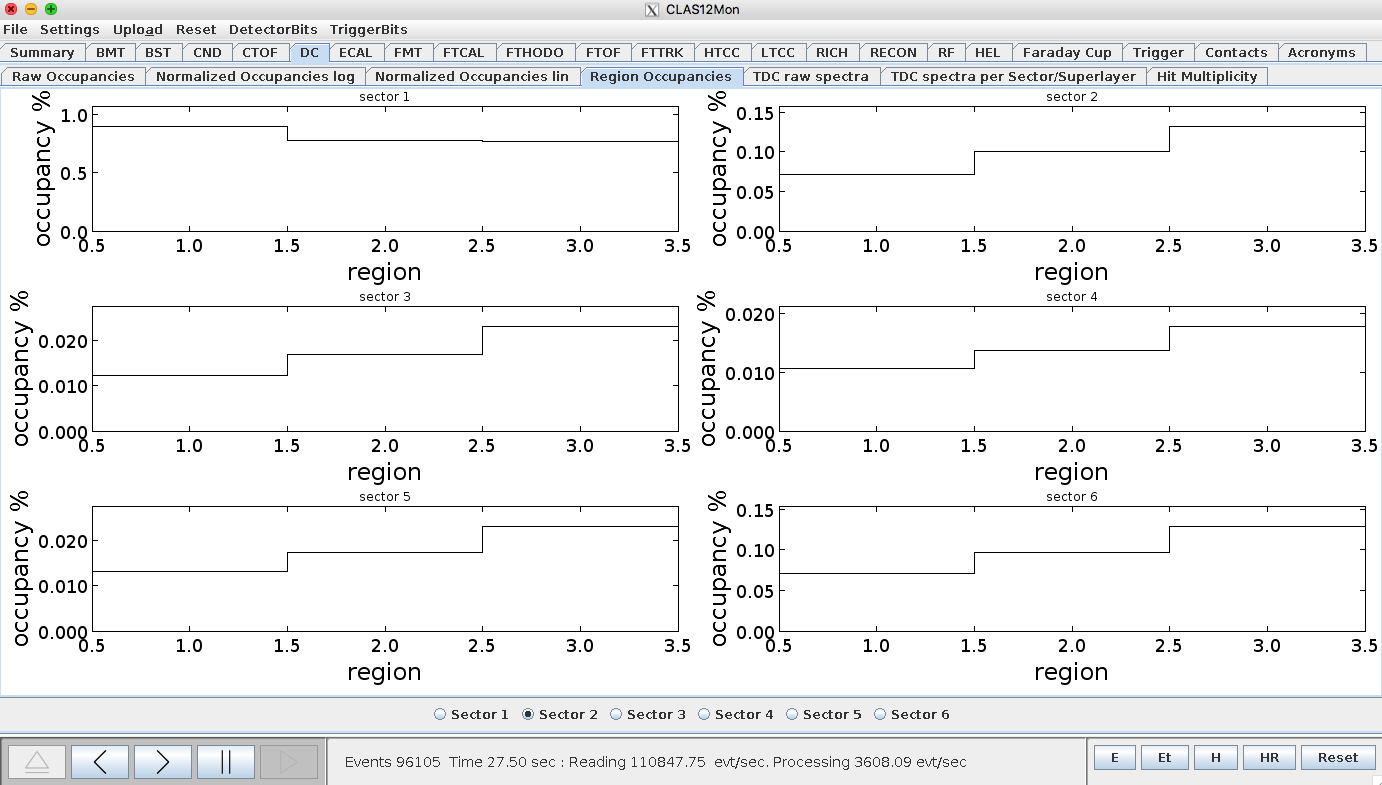
FOR DC Limits
Calculating
[math]\sigma_{Moller\ (\theta_{lab} = 5^{\circ}-40^{\circ})}=0.86\ barn[/math]
[math]t_{simulated}=\frac{N_{events}}{\sigma_{events} \Phi \rho \ell}=\frac{96105\ barn \cdot s}{7.87\times 10^{-2} \cdot 1.33\times 10^{11}\ barn}=9.3\times 10^{-6} s[/math]
[math]N_0=\Delta t \cdot R_{events}=\Delta t \cdot \frac{N_{events}}{t_{simulated}}=250\times 10^{-9}\ s \cdot \frac{98181}{9.3\times 10^{-6}\ s}=2639[/math]
[math]Occupancy=\frac{N_{hits}}{N_0}=\frac{N_{hits}}{\Delta t \cdot R_{events}}=\frac{t_{simulated}\cdot N_{hits}}{N_{events}\cdot \Delta t}=[/math]
Efficiency
Efficiency
