[math]\textbf{Navigation}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]
Using the values from Whitney:

For a 5cm target of LH2:
[math]\rho_{target}\times l_{target}=\frac{70.85 kg}{1 m^3}\times \frac{1 mole}{2.02 g} \times \frac{1000g}{1 kg} \times \frac{6.022\times10^{23} molecules\ LH_2}{1 mole} \frac{2 atoms}{1\ molecule\ LH_2} \times \frac{1m^3}{(100 cm)^3} \times \frac{5 cm}{ }=\frac{2.11\times 10^{23}}{cm^2} \times \frac{1^{-24} cm^{2}}{barn}=0.211 barns^{-1}[/math]
Using the beam current of 100nA,
[math]\Phi_{beam}=\frac{100\times 10^{-9}\ A}{1} \times \frac{1\ C}{1\ A} \times \frac{1\ e^{-}}{1\ s} \times \frac{1}{1.602\times 10^{-19}C}\Rightarrow 6.2422\times 10^{11}\ \frac{1}{s}=\Phi_{e^{-}}[/math]
Given the beam Luminosity of:
[math]\mathcal {L}=\frac{1.32\times 10^{35}}{cm^2 \cdot s}\frac{10^{-24} cm^{2}}{barn}=\frac{1.32\times 10^{11}}{barn\cdot s}=\Phi_{beam}\ \rho\ l_{target}[/math]
We can check to make sure the density makes sense
[math]\Rightarrow \rho_{target}=\frac{1.32\times 10^{35}}{ \Phi_{beam}\ l_{target}cm^2 \cdot s}=\frac{1.32\times 10^{35}}{ 6.24\times 10^{11}\ \cdot 5cm^3}=\frac{4.23\times 10^{22}}{cm^3}[/math]
[math]\Rightarrow \rho_{target}=\frac{70.85 kg}{1 m^3}\times \frac{1 mole}{2.02 g} \times \frac{1000g}{1 kg} \times \frac{6.022\times10^{23} molecules\ LH_2}{1 mole} \times \frac{1m^3}{(100 cm)^3}\frac{2 atoms}{1\ molecule\ LH_2}=\frac{4.23\times 10^{22}}{cm^3}[/math]
Using the values from Whitney :
https://wiki.iac.isu.edu/index.php/CLAS12_RateEst_byWA
Rates
| Energy |
6 GeV |
11 GeV
|
| Process |
(nb) |
(nb)
|
| Moller |
22773001 |
75008636
|
| DIS + radiative tail |
128 |
83
|
| Elastic e-p |
5511220 |
3670740
|
| Elastic radiative tail |
24705 |
12944
|
| π0 electro-production |
14802 |
17908
|
| π0 photo-production |
569 |
852
|
| π+ electro-production |
4032 |
5536
|
| π+ photo-production |
282 |
487
|
| π− electro-production |
2806 |
3843
|
| π− photo-production |
199 |
342
|
| Total |
2.83317E7 |
7.87214E7
|
[math]R_{events}= \sigma_{events} \mathcal{L}=7.87\times 10^{-2}\ barn\ \cdot \frac{1.33\times 10^{11}}{barn\cdot s}=\frac{1.05\times 10^{10}events}{s}[/math]
[math]R_{Moller}= \sigma_{Moller} \mathcal{L}=7.50\times 10^{-2}\ barn\ \cdot \frac{1.33\times 10^{11}}{barn\cdot s}=\frac{9.97\times 10^{9}Moller}{s}[/math]
File:CLAS12ExpWS WA.pdf


[math]\sigma=\frac{R}{\mathcal{L}}=\frac{dN}{dt}\cdot \frac{1}{\mathcal{L}}[/math]
[math]\Rightarrow \int\limits_{0}^{t}\, dt=\int\limits_{0}^{N}\frac{1}{\sigma \mathcal{L}}\, dN[/math]
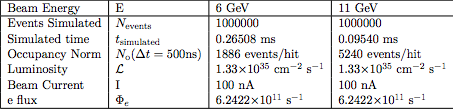
[math]t_{simulated}=\frac{N_{events}}{\sigma_{events} \Phi \rho \ell}=\frac{1000000\ barn \cdot s}{7.87\times 10^{-2} \cdot 1.33\times 10^{11}\ barn}=9.54\times 10^{-5} s[/math]
[math]N_0=\Delta t \cdot R_{events}=\Delta t \cdot \frac{N_{events}}{t_{simulated}}=500\times 10^{-9}\ s \cdot \frac{1\times 10^6}{0.0954\times 10^{-3}\ s}=5240[/math]
[math]Occupancy=\frac{N_{hits}}{N_0}=\frac{N_{hits}}{\Delta t \cdot R_{events}}=\frac{t_{simulated}\cdot N_{hits}}{N_{events}\cdot \Delta t}=[/math]
Similarly,
[math]N_{events} =R_{events}\cdot t_{simulated}=\frac{1.05\times 10^{10}events}{s} \cdot 9.54\times 10^{-5} s=1001700\ events[/math]
[math]N_{Moller} =R_{Moller}\cdot t_{simulated}=\frac{9.97\times 10^{9}Moller}{s} \cdot 9.54\times 10^{-5} s=951138\ Moller[/math]
[math]\sigma=\frac{ t\ N_{scattered}}{\Delta t N_{incident}}\frac{1}{\rho \ell}\Rightarrow N_{incident}=\frac{t\ N_{scattered}}{\Delta t\sigma \rho \ell}=\frac{0.0954\times 10^{-3}\ s\ \times 1000000}{250 \times 10^{-9}\ s \times .078\cdot 2.11\times 10^{-1}}\approx 6\times 10^7\ incident \times 380 \approx 2\times 10^10[/math]
[math]\left ( \frac{Number\ of\ hits}{Moller\ electron}\right ) \left (\frac{Moller\ electrons}{incidents\ electron} \right) \left (\frac{incident\ electrons}{sec} \right )[/math]







