[math]\textbf{\underline{Navigation}}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]
t Channel
The t quantity is known as the square of the 4-momentum transfer
[math]t \equiv \left({\mathbf P_1^*}- {\mathbf P_1^{'*}}\right)^2=\left({\mathbf P_2^{*}}+ {\mathbf P_2^{'*}}\right)^2[/math]
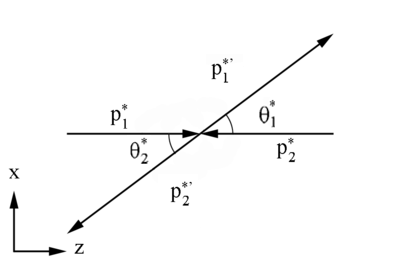
[math]t \equiv \left({\mathbf P_1^*}- {\mathbf P_1^{'*}}\right)^2[/math]
[math]t \equiv \mathbf P_1^{*2}-2 \mathbf P_1^* \mathbf P_1^{'*}+ \mathbf P_1^{'*2}[/math]
[math]t \equiv 2m_1^2-2E_1^*E_1^{'*}+2 \vec p \ _1^* \vec p \ _1^{'*}[/math]
In the center of mass frame of reference,
[math] E_1^*=E_1^{'*} \quad E_2^*=E_2^{'*} \quad E_1^*=E_2^*[/math]
and
[math]| \vec p \ _1^*|=| \vec p \ _1^{'*}| \quad | \vec p \ _2^*|=| \vec p \ _2^{'*}|[/math]
[math]t \equiv 2m_1^*-2E_1^{*2}+2 p \ _1^{*2}cos\ \theta[/math]
Using the relativistic term for Energy
[math]E^2=\vec p \ ^2+m^2[/math]
[math]t \equiv -2 p \ _1^{*2}(1-cos\ \theta)[/math]
[math]\textbf{\underline{Navigation}}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]
