DV Analyze Recon

Calculating kinematic variables in Moller Lab Frame

Finding the correct kinematic values starting from knowing the momentum of the Moller electron, $p^'_{2}$ , in the Lab frame,

xz Plane

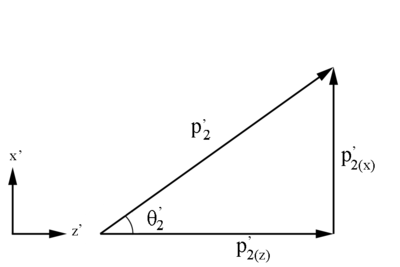Figure 1: Definition of Moller electron variables in the Lab Frame in the x-z plane.

Using $\theta '_2=\arccos \left(\frac{p^'_{2(z)}}{p^'_{2}}\right)$

$\Longrightarrow {p^'_{2(z)}=p^'_{2}\cos(\theta '_2)}$

Checking on the sign resulting from the cosine function, we are limited to:

$0^\circ \le \theta '_2 \le 60^\circ \equiv 0 \le \theta '_2 \le 1.046\ Radians$

Since,

$\frac{p^'_{2(z)}}{p^'_{2}}=cos(\theta '_2)$

$\Longrightarrow p^'_{2(z)}\ should\ always\ be\ positive$

xy Plane

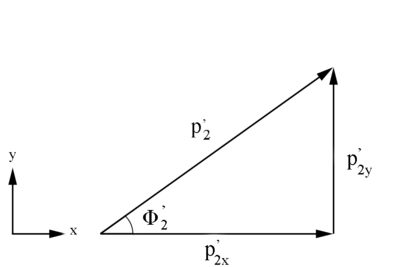Figure 2: Definition of Moller electron variables in the Lab Frame in the x-y plane.

Similarly, $\phi '_2=\arccos \left( \frac{p^'_{2(x) Lab}}{p^'_{2(xy)}} \right)$

where $p_{2(xy)}^'=\sqrt{(p_{2(x)}^')^2+(p^'_{2(y)})^2}$

$(p^'_{2(xy)})^2=(p^'_{2(x)})^2+(p^'_{2(y)})^2$

and using $p^2=p_{(x)}^2+p_{(y)}^2+p_{(z)}^2$

this gives $(p^'_{2})^2=(p^'_{2(xy)})^2+(p^'_{2(z)})^2$

$\Longrightarrow (p'_{2})^2-(p'_{2(z)})^2 = (p'_{2(xy)})^2$

$\Longrightarrow p_{2(xy)}^'=\sqrt{(p^'_{2})^2-(p^'_{2(z)})^2}$

which gives$\phi '_2 = \arccos \left( \frac{p_{2(x)}'}{\sqrt{p_{2}^{'\ 2}-p_{2(z)}^{'\ 2}}}\right)$

$\Longrightarrow p_{2(x)}'=\sqrt{p_{2}^{'\ 2}-p_{2(z)}^{'\ 2}} \cos(\phi)$

Similarly, using $p_{2}^2=p_{2(x)}^2+p_{2(y)}^2+p_{2(z)}^2$

$\Longrightarrow p_{2}^{'\ 2}-p_{2(x)}^{'\ 2}-p_{2(z)}^{'\ 2}=p_{2(y)}^{'\ 2}$

$p_{2(y)}'=\sqrt{p_{2}^{'\ 2}-p_{2(x)}^{'\ 2}-p_{2(z)}^{'\ 2}}$

$p_{x}$ and $p_{y}$ results based on $\phi$

Checking on the sign from the cosine results for $\phi '_2$

We have the limiting range that $\phi$ must fall within:

$-\pi \le \phi '_2 \le \pi\ Radians$

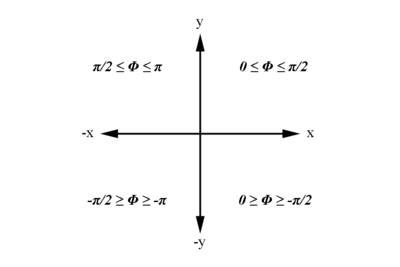
Examining the signs of the components which make up the angle $\phi$ in the 4 quadrants which make up the xy plane:

$For\ 0 \ge \phi '_2 \ge \frac{-\pi}{2}\ Radians$

px=POSITIVE

py=NEGATIVE

$For\ 0 \le \phi '_2 \le \frac{\pi}{2}\ Radians$

px=POSITIVE

py=POSITIVE

$For\ \frac{-\pi}{2} \ge \phi '_2 \ge -\pi\ Radians$

px=NEGATIVE

py=NEGATIVE

$For\ \frac{\pi}{2} \le \phi '_2 \le \pi\ Radians$

px=NEGATIVE

py=POSITIVE

We take the phi angle from the Generated Event momentum as the initial phi angle.

The obtain the final phi angle, we can look at the final position of the electron with in the drift chambers.

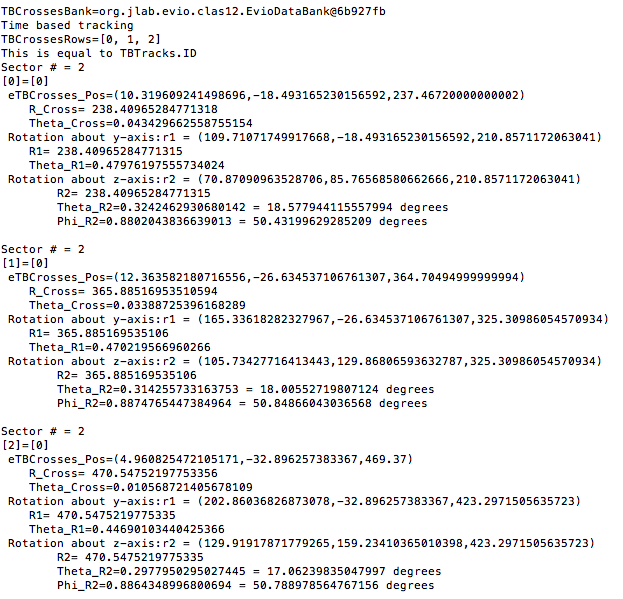
Examining the position from Timer Based Tracking, we can see that after rotations about first the y-axis, then the z-axis transforms from the detector frame of reference to the lab frame of reference.

Analysis.groovy

From a GEMC run of solenoid field strength of 0T, the eg12_rec.0.evio output file of the reconstruction is analyzed. The different kinematic variables are displayed as shown:

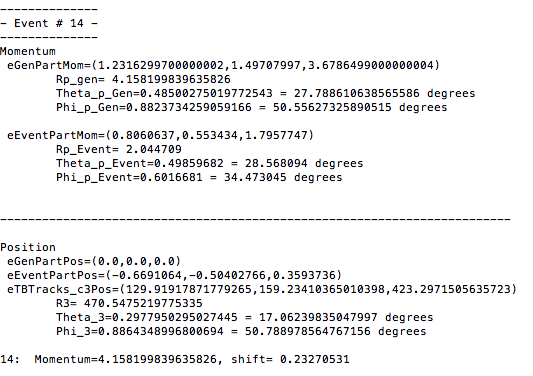
Using the phythagorean theorm to construct the Generated Event momentum vector length, we find:

$|\vec{p}_2\ '|=\sqrt{1.23162997^2+1.49707997^2+3.6786499^2}=4.15819983964$

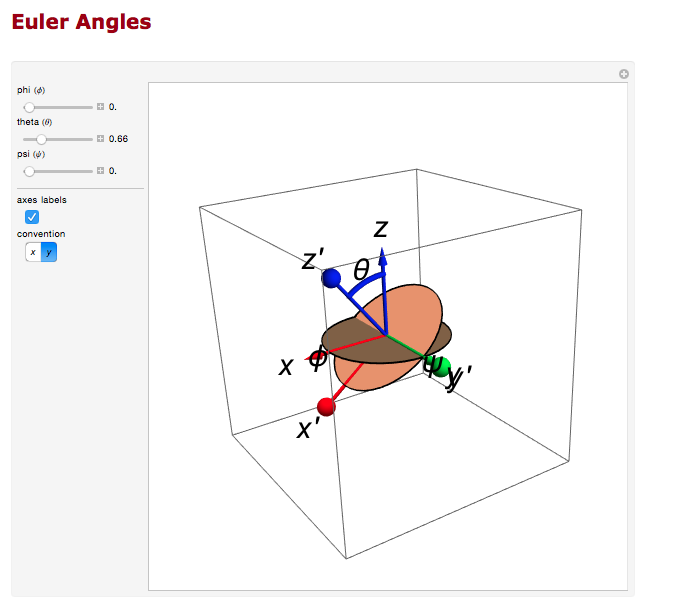
Euler Angles

We can use the Euler angles to perform the rotations.

For the rotation about the y axis.

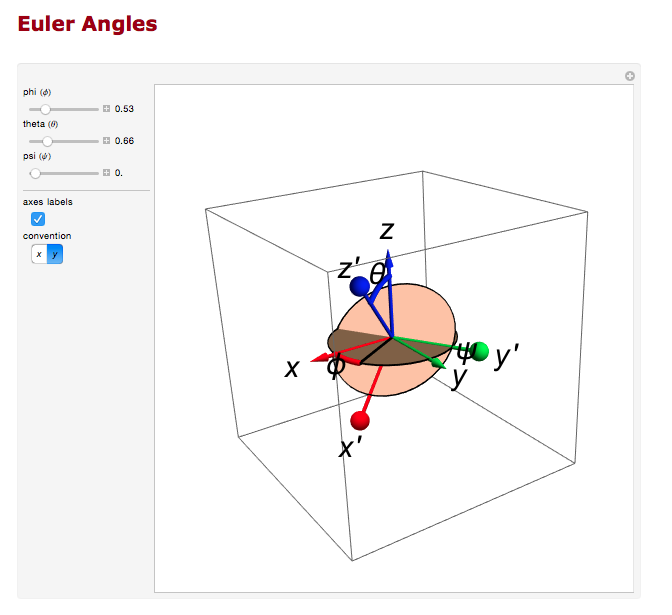
And the rotation about the z axis.

Transformation Matrix

The Euler angles can be applied using a transformation matrix

$\left( \begin{array}{ccc} \cos (\theta ) & 0 & -\sin (\theta ) \\ 0 & 1 & 0 \\ \sin (\theta ) & 0 & \cos (\theta ) \\ \end{array} \right).\left( \begin{array}{c} x \\ y \\ z \\ \end{array} \right)$$=\left( \begin{array}{c} x \cos (\theta )-z \sin (\theta ) \\ y \\ z \cos (\theta )+x \sin (\theta ) \\ \end{array} \right)$

For event #29, in sector 3, the location of the first interaction is given by

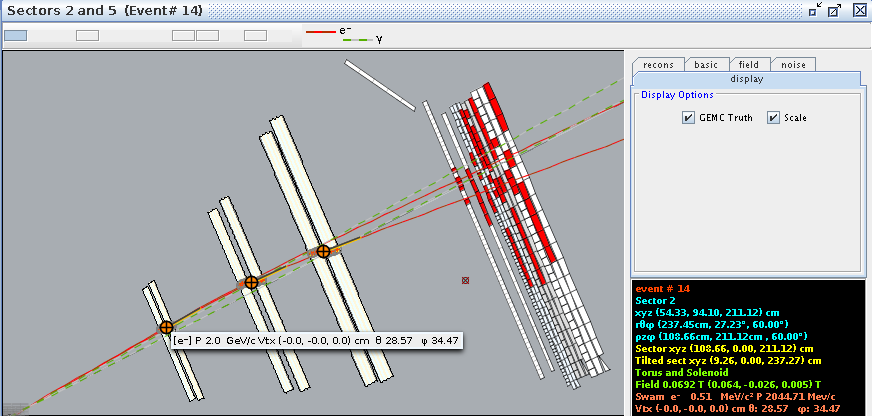
Converting -25 degrees to radians,

$\theta =-0.436332$

which is the rotation the detectors are rotated from the y axis.

$\left( \begin{array}{ccc} \cos (\theta ) & 0 & -\sin (\theta ) \\ 0 & 1 & 0 \\ \sin (\theta ) & 0 & \cos (\theta ) \\ \end{array} \right).\left( \begin{array}{c} -15.76 \\ 0 \\ 237.43 \\ \end{array} \right)$$=\left( \begin{array}{c} 86.0588 \\ 0. \\ 221.845 \\ \end{array} \right)$

Finding $\phi =\frac{120\ 2 \pi }{360};$ since "sector -1" =3-1=2*60=120 degrees

$\left( \begin{array}{ccc} \cos (\phi ) & -\sin (\phi ) & 0 \\ \sin (\phi ) & \cos (\phi ) & 0 \\ 0 & 0 & 1 \\ \end{array} \right).\left( \begin{array}{c} 86.0588 \\ 0. \\ 221.845 \\ \end{array} \right)$$=\left( \begin{array}{c} -43.0294 \\ 74.5291 \\ 221.845 \\ \end{array} \right)$

This shows how the coordinates are transformed and explains the validity of using the TBTracking information to obtain a phi angle in the lab frame.