DV MollerTrackRecon
Moller Lund
LUND file with Moller events (with origin of coordinates occurring at each event)
2 1 1 1 1 0 0.000563654 3.53715 0 6.2002 1 -1 1 11 0 0 0.69 -2.4999 10993.7998 10993.80 0.000511 0 0 0 2 -1 1 11 0 0 -0.69 2.4999 6.5852 7.08 0.000511 0 0 0
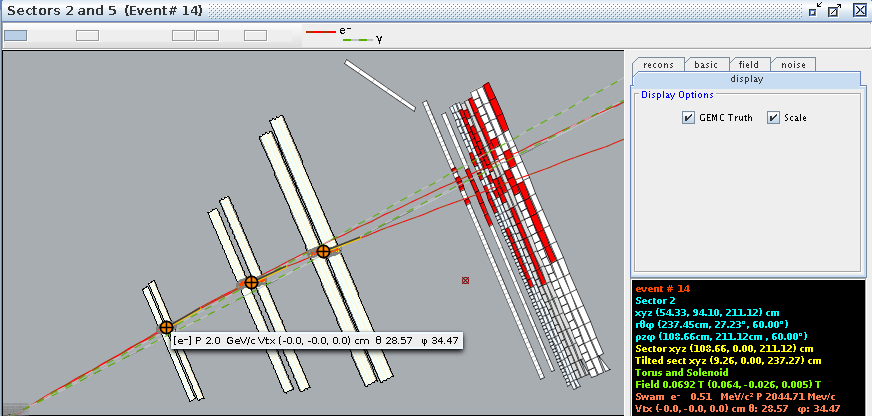
From a GEMC run WITH the Solenoid ced is used to obtain the information from the eg12_rec.ev file.
We take the phi angle from the Generated Event momentum as the initial phi angle. The obtain the final phi angle, we can look at the final position of the electron with in the drift chambers.
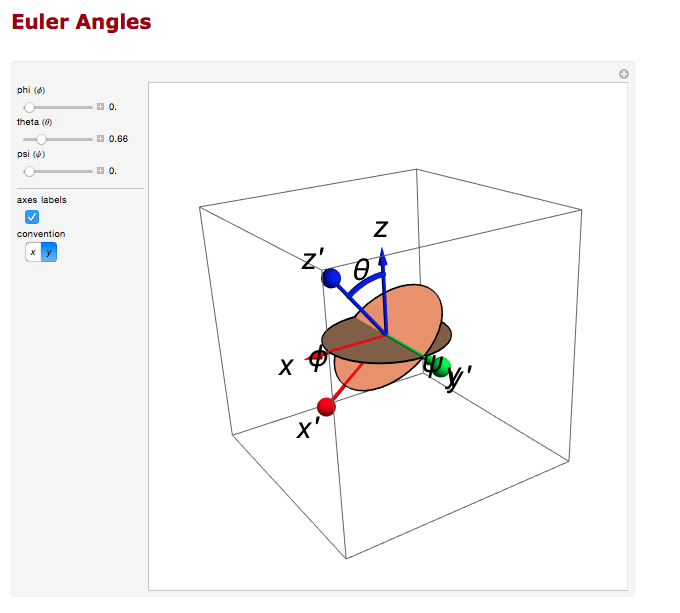
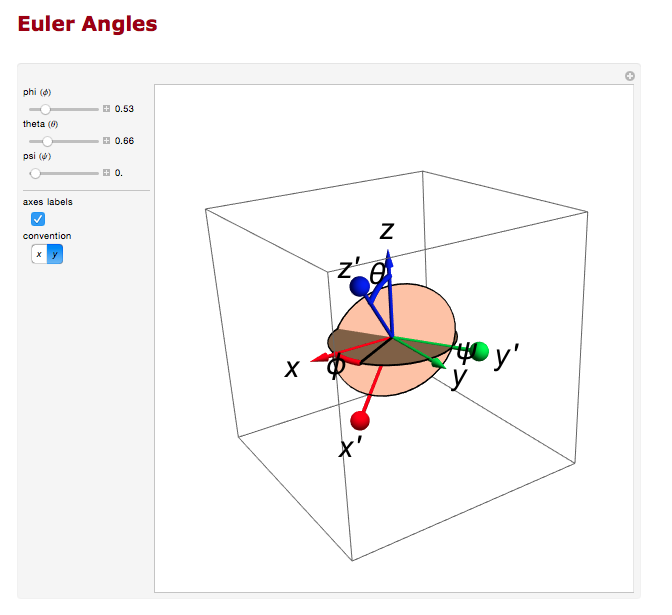
Examining the position from Timer Based Tracking, we can see that after rotations about first the y-axis, then the z-axis transforms from the detector frame of reference to the lab frame of reference.
Euler Angles
We can use the Euler angles to perform the rotations.
For the rotation about the y axis.
And the rotation about the z axis.
Transformation Matrix
The Euler angles can be applied using a transformation matrix
For event #29, in sector 3, the location of the first interaction is given by
Converting -25 degrees to radians,
which is the rotation the detectors are rotated from the y axis.
Finding since "sector -1" =3-1=2*60=120 degrees
This shows how the coordinates are transformed and explains the validity of using the TBTracking information to obtain a phi angle in the lab frame.
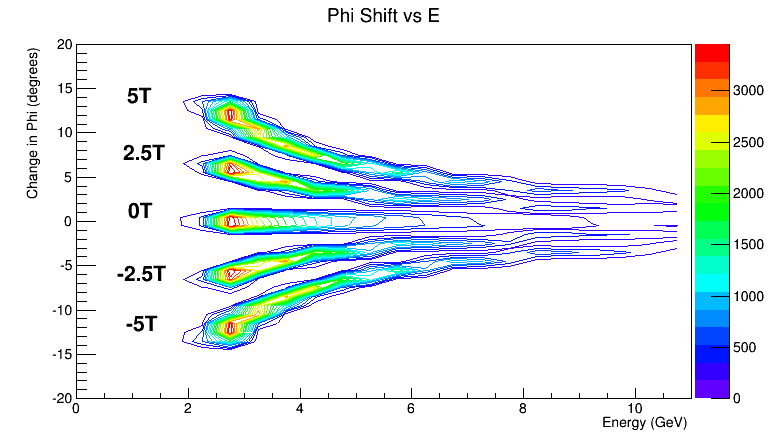
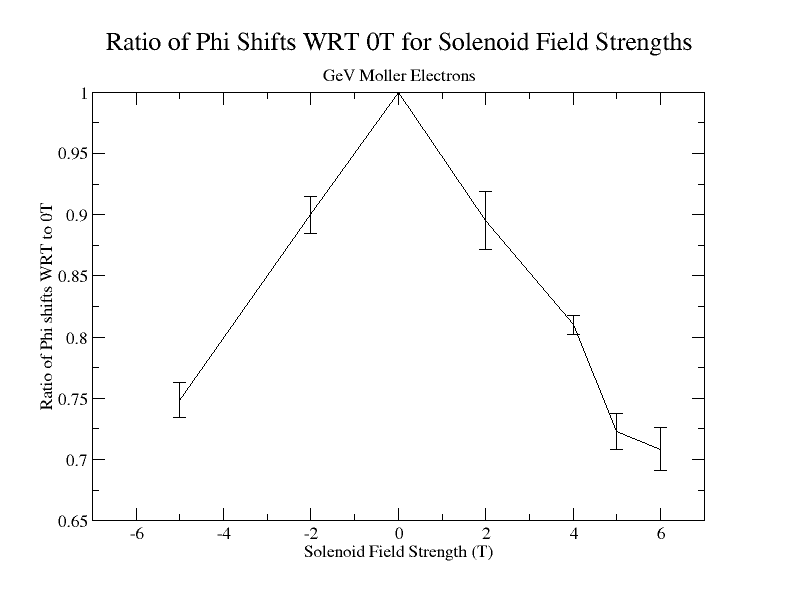
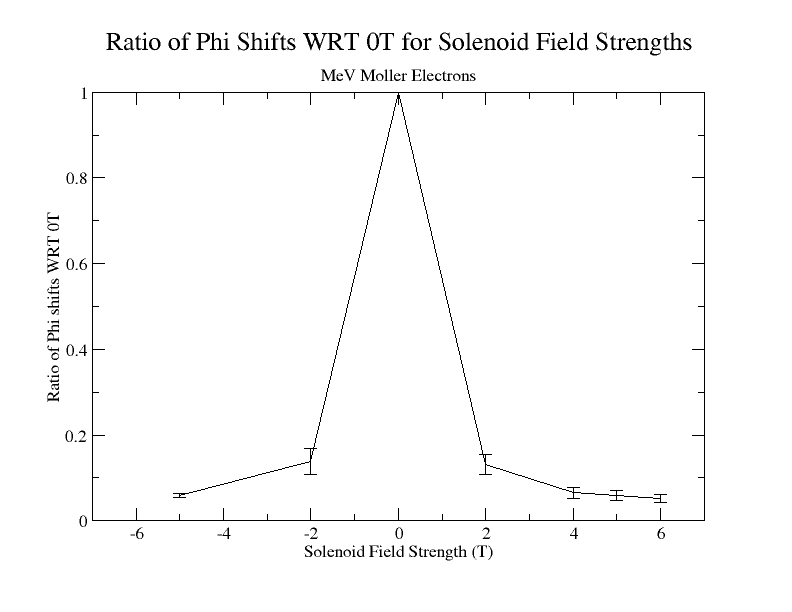
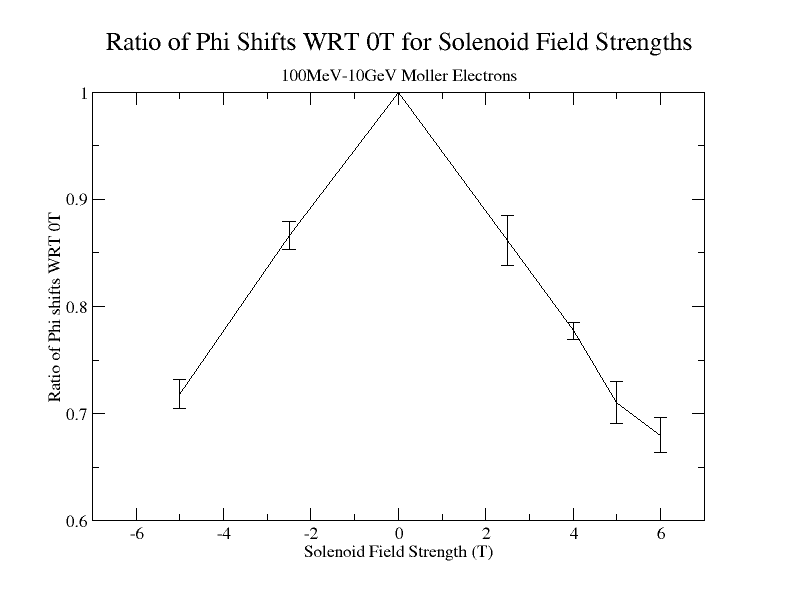
Phi shifts
gcard to generate electrons.
<option name="BEAM_P" value="e-, 6.0*GeV, 30.0*deg, 10*deg"> <option name="SPREAD_P" value="5.5*GeV, 25*deg, 180*deg">
Cross-section
Calculations of 4-momentum components (Trial 4)
Setup
Since we want to run for a evenly spaced energy range for Moller electrons, we will need to use some of the scattered electrons to help cover this range. A Moller scattering data file of 1E7 events has no Moller electrons with momentum over 5500 MeV. Since momentum is conserved, and the data is verified kinematicly verified, we cannot simply "switch" the data. This data can be altered to have a certain number of different phi values for each energy to match the Moller cross section. This data can then be written to a LUND file, and compared to the previous calculations which did not factor in loss of initial energy.
Prepare Data
Using the existing Moller scattering data from a GEANT simulation of 4E7 incident electrons, a file of just scattered momentum components can be constructed using:
awk '{print $9, $10, $11, $16, $17, $18}' MollerScattering_NH3_Large.dat > Just_Scattered_Momentum.dat
Transfer to CM Frame
Reading in the data from the dat file, we use a C++ program to read the momentum components for the Scattered and Moller electrons into 4-momentum vectors defined as the Lab_final frame of reference.
Performing a Lorentz boost to a Center of Mass frame for the two 4-vectors from the Lab_final frame of reference, we move to a frame where the energies are equal and the momentum are equal but opposite.
For Moller Electron energies above 500 MeV, in the Lab frame, histograms of momentum, and theta as well as a 2-D histogram of Energy vs. Theta for the Moller Electron in the CM frame will be filled.
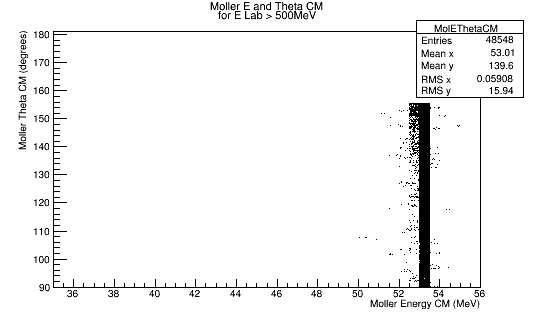
Using the histogram for Theta in the CM frame, we can determine the relative number of events that occur at a given angle. This information will be used to keep the relative number of particles having the same Theta angle, but multiple Psi angles to evenly cover the detector area
Run for Necessary Amount to match Cross Section
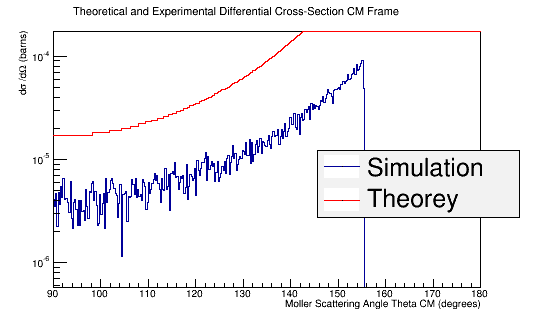
Using the above plot for the target material, we can find the relative amount that each Theta angle should observe for this process which gives a known Moller differential cross section.
| Theta (degrees) | Number of events |
|---|---|
| 90 | 5 |
| 100 | 5 |
| 110 | 6 |
| 120 | 8 |
| 130 | 12 |
| 135 | 20 |
| 140 | 28 |
| 142 | 30 |
| 144 | 40 |
| 146 | 45 |
| 148 | 55 |
| 150 | 70 |
| 152 | 80 |
| 154 | 100 |
We can set up conditional statements to check what range the Theta angle falls in, then by dividing
we should find the change in phi needed to give an evenly distributed distribution around the xy plane for a given Theta angle.
Alter Phi Angles
From a C++ program, random Energies and Angle Theta are read from the 2-D histogram created above. Using Relativistic kinematics for CM frame, a 4-momenta vector for the Moller electron is created. Using the properties of the CM frame, a 4-momenta vector for the scattered electron is created. Using the relative counts for number of events at a given angle theta in the CM frame, multiple copies of the Moller CM 4-momenta vector are created. Since the rotation of the angle Phi does not alter the z or total momentum, the same paired version of the scattered electron 4-momenta vector are transfered over from the Moller. Altering Phi Angles
Using two paired 4-momenta vectors in the CM frame, we can rotate them from the "CM-final" state to the "CM-initial" state by having the total momentum of each vector being held only in the z-component as would be expected for two colliding particles (). From this, a Lorentz boost can be performed to find the 4-vectors in the Lab frame for an incoming electron or various energies striking a stationary electron. With the boost vector a second Lorentz boost can be performed from the Final CM Frame to the Final Lab Frame. In this state, the phi distribution is unaffected by the Lorentz boost (perpendicular to direction of relativistic motion), while the theta angle is transformed.
10 separate trials were run for 10,000 events each. The histograms of Momentum, Angle Theta and Phi for the scattered and Moller electron in both the final lab frame and final CM frame were combined using:
hadd -f Total_MakeCM.root set1/MakeCM.root set2/MakeCM.root set3/MakeCM.root set4/MakeCM.root set5/MakeCM.root set6/MakeCM.root set7/MakeCM.root set8/MakeCM.root set9/MakeCM.root set10/MakeCM.root
Their LUND files were combined using
cat set1/Extra_Phi.LUND set2/Extra_Phi.LUND set3/Extra_Phi.LUND set4/Extra_Phi.LUND set5/Extra_Phi.LUND set6/Extra_Phi.LUND set7/Extra_Phi.LUND set8/Extra_Phi.LUND set9/Extra_Phi.LUND set10/Extra_Phi.LUND >Total_Extra_Phi.LUND
resulting in a LUND file that was 13294719 lines in length, which equates to 4431573 entries. This was divided into 177 file parts of 75000 each. The first set from the original data set is shown below.
split -a 4 -d -l 75000 Total_Extra_Phi.LUND Phi_Parts_

It was shown earlier that the differential cross section scale is
For an Ammonia target:
If the beam had 4E8 incident electrons, the differential cross-section would be found with,
Since extra Phi angles have been produced obviously a larger number of incident electrons would be needed. Looking at the number Moller events are created for 1E6, 1E7, and 4E8 incident electrons, we can estimate the number of incident electrons needed for the number of extra Phi angles produced.
Using the same expression, but this time for x? incident electrons,
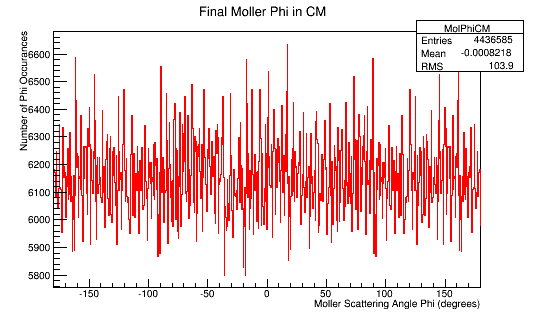
The Phi distribution for the CM and Lab frame.
Running LUND files in GEMC
Once the LUND file is broken into 177 parts, they can have the LUND extension added by:
prename 's/(Phi_Parts_\d{4})/$1.LUND/' Phi_Parts_*
Placing each of these files into its own directory
find . -name "*.LUND" -exec sh -c 'mkdir "${1%.*}" ; mv "$1" "${1%.*}" ' _ {} \;
Copying the submit0000 file into 177 files
for FILE in `seq 0001 0177`; do cp submit0000 submit$FILE; done
Differential Cross Section
Variables used in Elastic Scattering
Variables Used in Elastic Scattering