Forest UCM RBM

Rigid Body Motion

Rigid Body

Rigidy Body

A Rigid Body is a system involving a large number of point masses, called particles, whose distances between pairs of point particles remains constant even when the body is in motion or being acted upon by external force.

Forces of Constraint

The internal forces that maintain the constant distances between the different pairs of point masses.

Total Angular Momentum of a Rigid Body

Consider a rigid body that rotates about a fixed z-axis with the origin at point O.

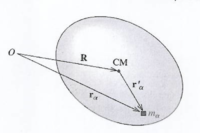
let

[math]\vec R[/math] point to the center of mass of the object

[math]\vec {r}_k[/math] points to a mass element [math]m_k[/math]

[math]\vec{r}_k^{\;\;\prime}[/math] points from the center of mass to the mass element [math]m_k[/math]

the angular momentum of mass element [math]m_k[/math] about the point O is given as

[math]\ell_k = \vec {r}_k \times \vec {p}_k = \vec {r}_k \times m \vec {\dot r}_k[/math]

The total angular momentum about the point O is given as

[math] \vec L = \sum \ell_k = \sum \vec {r}_k \times m_k \vec {\dot r}_k[/math]

This can be cast in term of the angular momentum about the center of mass and the angular momentum of the CM motion

[math]\vec {r}_k = \vec R + \vec{r}_k^{\;\; \prime}[/math]

[math] \vec L = \sum \vec {r}_k \times m_k \vec {\dot r}_k[/math]

[math] = \sum (\vec R + \vec{r}_k^{\;\; \prime}) \times m_k (\vec \dot R + \vec{\dot r}_k^{\;\; \prime})[/math]

[math] = \sum \vec R \times m_k \vec \dot R + \sum \vec R \times m_k \vec{\dot r}_k^{\;\; \prime} + \sum \vec{r}_k^{\;\; \prime} \times m_k \vec \dot R +\sum \vec{r}_k^{\;\; \prime} \times m_k \vec{\dot r}_k^{\;\; \prime} [/math]

[math]\sum \vec R \times m_k \vec \dot R = \vec R \times \sum m_k \vec \dot R = \vec R \times M \vec \dot R = \vec R \times \vec P[/math]

[math]\vec P =[/math] momentum of the center of Mass

[math]\sum \vec R \times m_k \vec{\dot r}_k^{\;\; \prime} = \vec R \times \sum m_k \vec{\dot r}_k^{\;\; \prime} 0[/math]

[math]\sum m_k \vec{\dot r}_k^{\;\; \prime} = \sum m_k \left ( \vec {r}_k - \vec R\right ) = \sum m_k \vec {r}_k - \sum m_k \vec R = \vec {v}_{cm} - \vec{v}_{cm} = 0[/math]

The location of the center of mass is at [math]\vec{ r}_k^{\;\; \prime} = 0[/math] the derivative is also zero

[math]\sum \vec{r}_k^{\;\; \prime} \times m_k \vec \dot R = \sum m_k \vec{r}_k^{\;\; \prime} \times \vec \dot R =0 [/math] : The location of the CM is at 0

[math] \vec L = \vec R \times \vec P + \sum \vec{r}_k^{\;\; \prime} \times m_k \vec{\dot r}_k^{\;\; \prime} [/math]

[math] = L_{\mbox{CM}} + L_{\mbox{about CM}} [/math]

The total angular momentum is the sum of the angular momentum of the center of mass of a rigid body [math] L_{\mbox{CM}} [/math] and the angular momentum of the rigid body about the center of mass [math] L_{\mbox{about CM}} [/math]

Planet example

What is the total angular momentum of the earth orbiting the sun?

There are two components

[math] \vec L_{\mbox{CM}} [/math] = angular momentum of the earth orbiting about the sun

[math] \vec L_{\mbox{about CM}} [/math] = angular momentum of the earth orbiting about the earth's center of mass (Spin)

[math]\vec L_{\mbox{tot}} = \vec L_{\mbox{CM}} + \vec L_{\mbox{about CM}}[/math]

[math] \vec L_{\mbox{CM}} [/math] is conserved and defined as Orbital angular momentum

[math]\vec \dot L_{\mbox{CM}} = \vec \dot R \times \vec P + \vec R \times \vec \dot P[/math]

[math]\vec \dot R \times \vec P = \vec V \times M \vec V = 0[/math]

[math]\Rightarrow \vec \dot L_{\mbox{orb}} = \vec R \times \vec \dot P=\vec R \times \vec {F}_{ext}[/math]

If there is only a central force

[math]\vec {F}(\mbox{ext}) = G \frac{Mm}{R^3} \vec R[/math]

Then

[math]\vec R \times \vec {F}(\mbox{ext}) = \vec R \times G \frac{Mm}{R^3} \vec R= G \frac{Mm}{R^3} \vec R \times \vec R =0 [/math]

Thus

[math]\vec \dot L_{\mbox{CM}} = \vec R \times \vec {F}(\mbox{ext}) = 0[/math]

[math]\vec L_{\mbox{CM}} \equiv \vec L_{\mbox{Orb}}[/math] = constant = Orbital angular momentum

The above is a good approximation even though the Sun's gravitational Field is not perfectly uniform

How about [math]\vec L_{\mbox{about CM}}[/math]?

Since

[math]\vec L_{\mbox{tot}} = \sum \vec {r}_k \times m_k \vec {\dot r}_k =\vec L_{\mbox{Orb}} + \vec L_{\mbox{about CM}}[/math]

as seen earlier

[math] \vec L = \sum \vec {r}_k \times m_k \vec {\dot r}_k[/math]

[math] = \sum (\vec R + \vec{r}_k^{\;\; \prime}) \times m_k (\vec \dot R + \vec{\dot r}_k^{\;\; \prime})[/math]

[math] = \vec R \times \vec P + \sum \vec{r}_k^{\;\; \prime} \times m_k \vec{\dot r}_k^{\;\; \prime} [/math]

Then

[math]\dot \vec L = \vec \dot R \times \vec P +\vec R \times \vec \dot P + \sum \vec{\dot r}_k^{\;\; \prime} \times m_k \vec{\dot r}_k^{\;\; \prime} + \sum \vec{r}_k^{\;\; \prime} \times m_k \vec{\ddot r}_k^{\;\; \prime} [/math]

[math] =\vec R \times \vec \dot P + \sum \vec{r}_k^{\;\; \prime} \times m_k \vec{\ddot r}_k^{\;\; \prime} [/math]

[math] =\vec R \times \vec {F}(\mbox{ext}) + \sum \vec{r}_k^{\;\; \prime} \times m_k \vec{\ddot r}_k^{\;\; \prime} [/math]

[math] =\vec{\dot{ L}}_{\mbox{Orv}} + \vec{\dot {L}}_{\mbox{about CM}}[/math]

[math]\Rightarrow \vec{\dot {L}}_{\mbox{about CM}} = \sum \vec{r}_k^{\;\; \prime} \times m_k \vec{\ddot r}_k^{\;\; \prime} [/math]

[math] \vec{\dot {L}}_{\mbox{spin}}\equiv\vec{\dot {L}}_{\mbox{about CM}} = \sum \vec{r}_k^{\;\; \prime} \times m_k \vec{\ddot r}_k^{\;\; \prime} \equiv \tau(\mbox{ext about CM}) [/math]

The total angular momentum is the sum of the orbital angular momentum and the spin

[math]\vec L_{\mbox{tot}} = \vec L_{\mbox{orb}} + \vec L_{\mbox{spin}}[/math]

Precession of the Earth

http://courses.physics.northwestern.edu/Phyx125/Precession%20of%20the%20Earth.pdf

Total Kinetic energy of a Rigid Body

Using the same coordinate system as above

the kinetic energy of mass element [math]m_k[/math] about the point O is given as

[math]T_k = \frac{1}{2} m_k \left | \vec \dot{r}_k \right |^2[/math]

The total Kinetic about the point O is given as

[math] \vec T = \sum \frac{1}{2} m_k \left | \vec \dot{r}_k \right |^2[/math]

Rewriting this again in terms of the location of the CM of the body [math]\vec R[/math] and the location of a mass element from the CM [math]\vec{r}_k^{\;\; \prime}[/math]

[math]\vec {r}_k = \vec R + \vec{r}_k^{\;\; \prime}[/math]

[math]\vec {\dot r}_k = \vec \dot R + \vec{\dot r}_k^{\;\; \prime}[/math]

[math]\vec {\dot r}_k \cdot \vec {\dot r}_k = \left ( \vec \dot R + \vec{\dot r}_k^{\;\; \prime} \right ) \cdot \left ( \vec \dot R + \vec{\dot r}_k^{\;\; \prime} \right ) [/math]

[math] = \left | \vec \dot R \right |^2 + \left | \vec{\dot r}_k^{\;\; \prime} \right |^2 + 2 \vec \dot R \cdot \vec{\dot r}_k^{\;\; \prime} [/math]

[math] \vec T = \sum \frac{1}{2} m_k \left | \vec \dot{r}_k \right |^2[/math]

[math] = \sum \frac{1}{2} m_k \left | \vec \dot R \right |^2 + \left | \vec{\dot r}_k^{\;\; \prime} \right |^2 + 2 \vec \dot R \cdot \vec{\dot r}_k^{\;\; \prime}[/math]

[math] = \frac{1}{2} M \left | \vec \dot R \right |^2 + \frac{1}{2} \sum m_k \left | \vec{\dot r}_k^{\;\; \prime} \right |^2 + \vec \dot R \cdot \sum m_k \vec{\dot r}_k^{\;\; \prime}[/math]

For a Rigid body

[math] \sum m_k \vec{\dot r}_k^{\;\; \prime} =0 [/math] The internal kinetic energy is zero for a rigid body, otherwise it would be expanding

[math] \vec T = \frac{1}{2} M \left | \vec \dot R \right |^2 + \frac{1}{2} \sum m_k \left | \vec{\dot r}_k^{\;\; \prime} \right |^2 \cdot [/math]

[math] = T_{\mbox{CM}} + T_{\mbox{about CM}}[/math]

Total Potential energy of a Rigid Body

If all forces are conservative

[math]\vec \nabla \times \vec F_{ij} = 0[/math]

then a Potential Energy may be defined

[math]\Delta U_{ij}(r_{ij}) \equiv -\int_{r_o}^r \vec{F}_{ij}(r_{ij}) \cdot d\vec{r}_{ij} = - W_{cons}[/math]

Then the potential energy of a rigid body is given by

[math]\sum_{i\lt j} \Delta U_{ij}(r_{ij}) = U_{\mbox{int}} = [/math] constant

for a rigid body the inter-particle separation distance [math]r_{ij}[/math] is constant so the internal potential of a rigid body does not change

Thus the kinematics of a Rigid body only needs to consider the potential energy of external forces.

Rotation about a fixed axis

Consider a Rigid body rotating with a speed [math]\vec \omega[/math] about a fixed axis (z-axis) with its origin at the point O

[math]\vec \omega = \omega \hat k[/math]

The total angular momentum about the point O is given as

[math] \vec L = \sum \ell_k = \sum \vec {r}_k \times m_k \vec {\dot r}_k[/math]

As seen in the non-inertial reference frame chapter

[math]\vec \dot r = \vec v = \vec \omega \times \vec r[/math]

thus

[math] \vec \omega \times \vec r_k = \left( \begin{array}{ccc} \hat i & \hat j & \hat k\\ 0 & 0 & \omega \\x_{k} & y_{k} & z_{k}\end{array} \right)= \omega \left ( - y_{k} \hat i + x_{k} \hat j \right ) [/math]

[math] \vec {r}_k \times \vec {\dot r}_k = \vec {r}_k \times \vec \omega \times \vec r = \vec {r}_k \times \omega \left ( - y_{k} \hat i + x_{k} \hat j \right ) [/math]

[math]= \left( \begin{array}{ccc} \hat i & \hat j & \hat k\\ x_{k} & y_{k} & z_{k} \\ -\omega y_{k} & \omega x_{k} & 0\end{array} \right)= \omega \left ( - z_{k}x_{k} \hat i - z_{k}y_{k} \hat j + \left (x_{k}^2+y_{k}^2 \right ) \hat k \right ) [/math]

[math] \vec L = \sum \ell_k = \sum \vec {r}_k \times m_k \vec {\dot r}_k[/math]

[math] = \omega \sum m_k \left ( - z_{k}x_{k} \hat i - z_{k}y_{k} \hat j + \left (x_{k}^2+y_{k}^2 \right ) \hat k \right )[/math]

Moments (Products) of Inertia about the fixed axis

[math]L_z = \omega \sum m_k \left (x_{k}^2+y_{k}^2 \right )[/math]

Let

[math]I_{zz} \equiv \sum m_k \left (x_{k}^2+y_{k}^2 \right ) =[/math] moment of inertia about the z-axis in the "z" ([math]\hat k[/math]) direction.

Then

[math]L_z = I_{zz} \omega[/math]

Similarly

Products of Inertia of a rigid body rotating about the z-axis for the angular momentum along the x-axis

[math]I_{xz} \equiv \sum m_k(x_{k} z_{k} [/math]

Products of Inertia of a rigid body rotating about the z-axis for the angular momentum along the y-axis

[math]I_{yz} \equiv \sum m_k \left (x_{k}^2+y_{k}^2 \right ) [/math]

[math] \vec L =\omega \left ( I{xz} \hat i + I{yz} \hat k + I{zz} \hat k \right )[/math] = angular momentum about the z-axis

Forest_Ugrad_ClassicalMechanics#Rigid_Body_Motion