Forest UCM Ch3 Rockets

Consider a rocket of mass [math]m[/math] moving at a speed [math]v[/math] ejecting rocket fuel for propulsion.

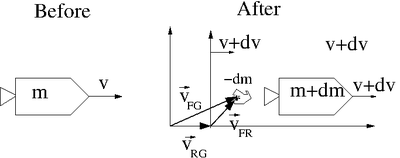File:Forest UCM Ch3 Rockets Fig.xfig.txt

[math]m =[/math] mass of Fuel + Rocket

[math]-dm =[/math] mass of Fuel ejected over time interval [math]dt[/math] ( [math]dm[/math] = mass lost by rocket < 0)

[math]u =v_{FR}[/math] velocity of Fuel relative to the Rocket

[math]v =[/math] velocity of rocket relative to the ground before ejecting fuel of mass [math](-dm)[/math]

[math]v+dv =v_{RG}[/math] velocity of the rocket relative to the ground after ejecting fuel

[math]V_FG =[/math] Velocity of the fuel with respect to the ground

Apply Conservation of Momentum

[math]mv = (-dm)V_{FG} + (m-(-dm))(v+dv)[/math]

[math]dmV_{FG} = mdv + dm (v+dv)[/math]

The velocity of the fuel with respect to the ground[math] (V_{FG})[/math] may be written as the vector sum of the rocket's velocity with respect to the ground [math](V_{RG})[/math] and the velocity of the fuel with respect to the rocket [math](V_{FR})[/math] :Galilean transormation

[math]\vec{V}_{FG} - \vec{V}_{FR} + \vec{V}_{RG}[/math]

assuming 1-D motion and using the velocity variables defined above

[math]V_{FG} = -u + (v+dv)[/math]

substituting

[math]dm \left (-u + (v+dv) \right ) = mdv + dm (v+dv)[/math]

[math]-udm = mdv [/math]

solving for the velocity

[math]\int_{v_0}^v = \int_{m_0}^m -u \frac{dm}{m}[/math]

[math]v - v_0 = u \ln \left (\frac{m_0}{m} \right )[/math]

Forest_UCM_MnAM#Rockets