TF EIM Chapt9

Operational Amplifiers (Op Amps)

The operational amplifier is monolithic (single chip) integrated circuit composed of transistors, resistors, diodes, and other components.

The small package produces a device with small capacitance and inductance which is superior to assembling the equivalent circuit with individual components.

Op-Amp

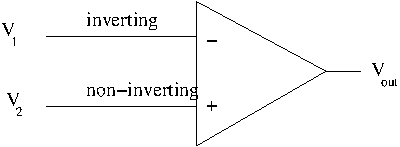
the "-" sign indicates the inverting input terminal and the "+" indicates the non-inverting input.

A positive going input voltage at the non-inverting ("+") input produces a positive going output.

A positive going input voltage at the inverting ("+") input produces a negative going output.

In other words the output is in phase when the input is non-inverting and 180 degrees out of phase when the input is inverting.

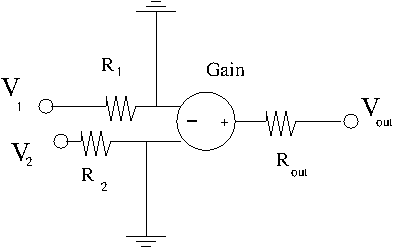
Equivalent circuit

Gain = [math]A_o \equiv \frac{V_{out}}{V_2-V_1} \equiv[/math] Open loop gain = gain when there isn't anything hooked up to the op amp to draw current from it.

Common Mode

Common mode input is defined as the situation where the two inputs are equal ([math]V_1 = V_2)[/math]. In this case[math] V_1[/math] is inverted and will cancel the input [math]V_2[/math] so the output becomes Zero in the ideal Op Amp.

Op Amps usually has two bias supplies in order to produce a high gain as determined by the difference in the input voltages. The output can't be larger than the supply bias.

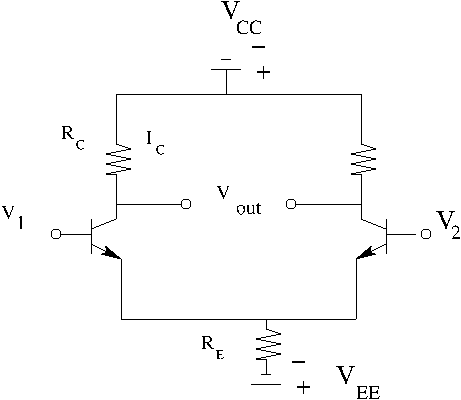
Differential Op Amp

A single stage differential op Amp can be described as being composed of two bipolar transistors in a common emitter configuration as shown below.

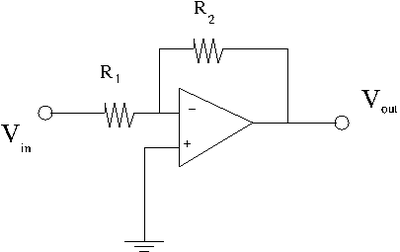
Inverting Amplifier

The above circuit is called an inverting amplifier. The input signal is applied to the inverting terminal ("-", [math]V_1[/math], or[math] V_n[/math]) of the Op Amp through a resister R_1. The non-inverting terminal ("+",[math] V_2[/math], or[math] V_p[/math] ) is grounded.

Applying the current junction rule at the inverting terminal one would have.

[math]I_1[/math]= current through resistor [math]R_1[/math] =[math] \frac{ V_1-V_{in}}{R_1}[/math]

[math]I_2[/math] = current through [math]R_2[/math] = [math]\frac{V_{out}-V_1}{R_2}[/math]

[math]I_{B1}[/math] = current entering the inverting terminal [math]V_1[/math] (the base of the bipolar transistor)

Current conservation \Rightarrow

[math]I_1 = I_2 + I_{B1}[/math]

or

[math]\frac{ V_1-V_{in}}{R_1} =\frac{V_{out}-V_1}{R_2} +I_{B1}[/math]

A "perfect" Op Amp has [math]I_{B1} = 0[/math]

[math]\frac{ V_1-V_{in}}{R_1} =\frac{V_{out}-V_1}{R_2} [/math]

Using the equivalent circuit from above

[math]V_{out} = A_0(V_2 - V_1)[/math]

Since [math]V_2 = 0[/math] for the inverting amplifier circuit above

[math]\frac{ -\frac{V_{out}}{A_0}-V_{in}}{R_1} =\frac{V_{out}+\frac{V_{out}}{A_0}}{R_2} [/math]

[math]\Rightarrow \frac{ -\frac{1}{A_0}-\frac{V_{in}}{V_{out}}}{R_1} =\frac{1+\frac{1}{A_0}}{R_2}[/math]

[math]\frac{V_{in}}{V_{out}} =-\frac{1}{A_0}-R_1 \frac{1+\frac{1}{A_0}}{R_2}[/math]

[math]= -\frac{R_2}{A_0R_2}-R_1 \frac{A_0+1}{A_0R_2}[/math]

[math]= -\frac{R_2 + R_1 (A_0+1)}{A_0R_2}[/math]

Gain[math]\equiv \frac{V_{out}}{V_{in}} = - \frac{A_0 R_2}{R_1(A_0+1) + R_2}[/math]