Matter Waves (Wave Particle Duality)
Special relativity said that
[math]E = pc[/math] if m=0
Plank said he could fit the Black Body radiation data assuming that that
[math]E= hf[/math] where [math]h = 6.63 \times 10^{-34} \mbox{ J} \cdot \mbox{s}[/math] = Plank's constant
Combining the two we have
[math] p=\frac{E}{c} = \frac{ h f}{c}[/math]
[math]\Rightarrow[/math] photons have momentum like a particle (mv)
Do particles reciprocate and behave like photons?
De Broglie's Hypothesis
If photons can behave like particles by having momentum
Then can a particle behave like a wave by having wavelength
[math] p=\frac{ h f}{c} = \frac{h}{\lambda}[/math]
or
[math]\lambda_{particle} = \frac{h}{p}=[/math] de Broglie Hypothesis
Davisson and Germer
We know that X-rays having a wavelength of [math]\lambda_{X-rays} = 7.1 \times 10^{-11} \mbox{m}[/math] make an interference patter on an aluminum foil.

[math]p_{X-ray} = \frac{h}{\lambda} = \frac{6.63 \times 10^{-34} \mbox{ J} \cdot \mbox{s}}{7.1 \times 10^{-11}\mbox{m}} \frac{1 \mbox{eV}}{1.6 \times 10^{-19} \mbox{J}}[/math]
- [math]= 5.8 \times 10^{-4} \frac{3 \times 10^{8}\mbox{m/s}}{c}[/math]
- [math]= 1.75 \times 10^{4} \frac{\mbox{eV}}{c}[/math]
- [math]= 17.5 \frac{\mbox{keV}}{c}\Rightarrow \mbox{E}=17.5 \mbox{keV}[/math]
Another way to calculate
[math]p_{X-ray} = \frac{hc}{\lambda c} = \frac{1240\mbox{ eV} \cdot \mbox{nm}}{0.071 \mbox{nm}\cdot \mbox{c}}= 17.5 \frac{\mbox{keV}}{c}[/math]
- What would be the energy of an electron with the same wavelength as the above X-ray?
relativistic total energy relation
- [math]E_{tot} = \sqrt{(pc)^2 + (mc^2)^2}[/math]
- [math]= \sqrt{(17.5 keV)^2 + (511 keV)^2}[/math]
- = 511.3 keV
relativistic kinetic energy
- [math]K = E - mc^2 = (\gamma-1)mc^2 = 0.3 \mbox{keV} = 300 \mbox{eV}[/math]
Hit a crystal made of nickel with 54 eV electrons.
1.) 54 eV electrons
From hyperphysics:
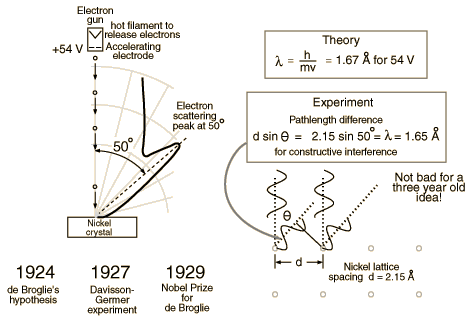
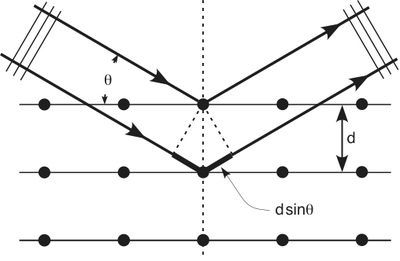
Bragg Diffraction
[1] Forest_Classes


