Se170063 Nickel Foil Wide Gauss Window Expansion

This analysis was done by weighting the histogram by the mass of the sample. The window is [1356,1368] and was expanded by one channel on each side to find the error in the counts.

	5/25/17	5/26/17	5/27/17	5/29/17	5/30/17	5/31/17	6/1/17
Original Window Counts	98320	173200	228300	85940	148900	109100	64250
Original Window Background (Integrated)	3954.6	8499.51	19328.4	2969.18	8652.05	5097.77	2584.57
Original Window Difference	94365.4	164700.49	208971.6	82970.82	140247.95	104002.23	61665.43
Expanded Window Counts	98870	174300	230500	86340	149900	109700	64540
Expanded Window Background	4058.92	8644.64	19114.1	3150.02	8755.1	5390.22	2565.2
Expanded Window Difference	84811.48	165655.36	211385.9	83189.98	141144.9	104309.78	61974.8
Error in counts	446.08	954.87	2414.3	219.16	896.95	307.55	309.37
Position	50 cm	30 cm	20cm	20 cm	10cm	10cm	10cm
Efficiency	0.00017	0.000422	0.000847	0.000847	0.0031	0.0031	0.0031
.dat file entry	14.42641264 +/- 0.0047271564	14.07896028 +/- 0.0057976148	13.5315612 +/- 0.0115532446	12.69531211 +/- 0.0026414106	12.01862017 +/- 0.0063922503	11.62243763 +/- 0.0029571481	11.07892229 +/- 0.0050169114

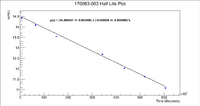
Below is a plot of the activity as a function of time

This gives the constant of 14.5046 +/- 0.00345043. Now find the initial activity

[math] A_t = e^{14.5046} = 1991900.96 Hz [/math]

<math> A_0 = A_{t}*e^{\lambda*}