ISU Coloq 11-3-2014

Abstract

ISU's intermediate energy nuclear physics group is presently involved in several fundamental physics measurements. This talk will describe a program to measure the fractional polarization of down quarks in a nucleon using polarized electrons to probe polarized nucleon targets. Quantum chromodynamcs (QCD) is a theory of the strong interaction; one of the four fundamental forces in nature. QCD predicts that the down quark will carry all of the nucleon's spin and result in a fractional polarization of unity when the probe interacts with down quarks that carry all of the nucleon's momentum. This theory contradicts the leading constituent quark model of the nucleon. The world's current set of data has yet to determine the veracity of either model. A description of this experimental program and the roles of ISU graduate students will be described.

electron scattering (collisions)

Elastic Collisions: Conserve P and E

Inelastic : Only Conserve P

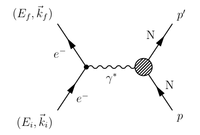
Definition of Momentum Transfer

Using Ryder 4-momentum tensor convention: [math]P_{\mu} \equiv (E/c, -\vec{p}) \;\;\;\;\; P^{\mu} \equiv (E/c, \vec{p})[/math]

[math]q_\mu \equiv (\omega, \vec{q})[/math] [math]k^i_\mu \equiv (E_i, \vec{k_i})[/math] [math]k^f_\mu \equiv (E_f, \vec{k_f})[/math]

Conservation of Momentum

[math] k^i_\mu =q_\mu + k^f_\mu [/math]

Momentum Transfer

[math] q_\mu =k^i_\mu - k^f_\mu [/math]

Momentum Transfer Squared

[math] -Q^2 = q^2 = q_\mu q^{\mu} =(E_i-E_f)^2 - (\vec{k}_i - \vec{k}_f) \cdot (\vec{k}_i - \vec{k}_f) [/math]

[math]= m_i^2 + m_f^2 -2E_iE_f + 2\left | \vec{k}_i\right | \left | \vec{k}_f\right | cos(\theta)[/math]

[math]=-4E_iE_f \sin^2(\theta/2) \;\;\; m_i = m_f \ll E_i \mbox{ and } E \approx \left | \vec{k}_i\right |[/math]

[math]Q^2 =4E_iE_f \sin^2(\theta/2) \gt 0[/math] A space-like scattering event

Space-like interval: Two events are separated by a space like interval then there isn't enough time passing between them to allow a cause-effect relationship because a photon can't traverse the distance. This means that there is no reference frame that may be used to describe the event as happening at the same spatial location but there is a frame that describes them happening at the same time. If the spacetime interval between the two events is defined as s[math]^2 = (\Delta r)^2 - (c\Delta t)^2[/math] then [math]s^2 \gt 0[/math] for a space-like interval

Time-like interval: Two events are separated by a time like interval if enough time passes between them to allow a cause-effect relationship. This means that there is no reference frame that may be used to describe the event as happening at the same time but there is one that describes them happening at the same spatial location. If the spacetime interval between the two events is defined as s[math]^2 = (\Delta r)^2 - (c\Delta t)^2[/math] then [math]s^2 \lt 0[/math] for a time-like interval

4-Momentum vector definition using Ryder convention

[math]P_{\mu} \equiv \left ( \frac{E}{c} , - \vec p \right )[/math]

[math]P^{\mu} \equiv \left ( \frac{E}{c} , \vec p \right )[/math]

[math]P_{\mu} P^{\mu} = \left ( \frac{E}{c}\right )^2 - \vec p^2 = E^2-p^2 = m^2[/math] if you define the speed of light as unity

Note

Other conventions used by Perkins

[math]P_{\mu} \equiv \left ( \vec p, -E \right )[/math]

[math]P^{\mu} \equiv \left ( \vec p , E\right )[/math]

or Kollen

[math]P_{\mu} \equiv \left ( \vec p, iE \right )[/math]

[math]P^{\mu} \equiv \left ( \vec p , iE\right )[/math]

Momentum transfer is defined as

[math]q_{\mu} \equiv ( \omega, \vec q) = P^i_{\mu} - P^f_{\mu}[/math] : conservation of momentum

[math]q_{\mu}q^{\mu} = (E_i - E_f)^2 - (\vec {P}_i - \vec{P}_f) \cdot (\vec {P}_i - \vec{P}_f)[/math]

[math]= m_i^2 +m_f^2 - 2E_iE_f + 2 \left | \vec {P}_i \right | \left | \vec {P}_f \right |[/math]

Definition of Missing Mass

Inelastic scattering (Energy is not conserved but absorbed from the momentum transfer)

[math]P_e^{\mu} \equiv (E_i,\vec{k}_i)[/math] [math]\left(P_e^{\mu}\right)^{\prime} \equiv (E_f,\vec{k}_f)[/math] [math]P_p^{\mu} \equiv (M_p,0)[/math] [math]\left(P_p^{\mu}\right)^{\prime} \equiv (E_X,\vec{k}_X)[/math]

4-momentum conservation

[math]P_e^{\mu} + P_p^{\mu} = \left(P_e^{\mu}\right)^{\prime} + \left(P_p^{\mu}\right)^{\prime}[/math]

[math]\left(P_p^{\mu}\right)^{\prime} \left(P_{\mu}^p\right)^{\prime} = [P_e^{\mu} + P_p^{\mu} - \left(P_e^{\mu}\right)^{\prime} ][P^e_{\mu} + P^p_{\mu} - \left(P^e_{\mu}\right)^{\prime} ][/math]

[math]E_X^2 - P_X^2 \equiv W^2 = (E_i^2 - k_i^2) + (E_f^2-k_f^2) + M_p^2 + 2M_p(E_i - E_f) -2(E_iE_f-\vec{k_i}\cdot \vec{k_f})[/math]

[math]W^2=M_p^2 + 2M_p(E_i-E_f) -Q^2 \equiv [/math]Invariant Missing Mass = mass of the intermediate state that was created.

200 px

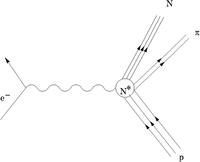
The Delta Resonance

Decay Modes: [math]ep \rightarrow \;\; \left \{ {N \pi \;\;\; 99.5% \atop p \gamma \;\;\; 0.5% } \right .[/math]

[math]\sigma = \lt \Delta^+ | V_{\mu}^3| p\gt [/math]

[math]V_{\mu}^3 =[/math] Vector current of the virtual photon exchange

Spin 1/2 and 3/2 final states

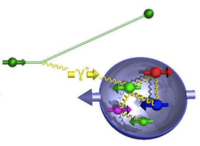
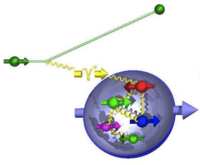
Double Spin Asymmetry

If both the target and the incident virtual photon are polarized then one can measure the cross-section for two separate conditions; when the spins are parallel and anti-parallel.

Let [math]\sigma_{3/2} [/math]

[math]\sigma_{1/2} \equiv[/math] photon helicity is anti-parallel to the target spin

[math]\sigma_{3/2} \equiv[/math] photon helicity is parallel to the target spin.

[math]\sigma_{\frac{1}{2}}[/math](Struck quark spin is [math]\parallel[/math] to Nucleon spin)	[math]\sigma_{\frac{3}{2}}[/math] (Struck quark spin is [math]\not\parallel[/math] to Nucleon spin)

Clebsch Gordan recoupling

The recoupling of two subsystems [math]\psi[/math] with angular momenta [math]j_1[/math] and [math]j_2[/math] to a new system[math] \Psi[/math] with total angular momentum [math]J[/math] is written as

[math]\Psi^{J}_{M} = \sum_{m_1=-j_1}^{j_1} \sum_{m_2=-j_2}^{j_2} C^{j_1\;,\;j_2,\;\;J}_{m_1,m_2,M} \; \psi^{j_1}_{m_1} \psi^{j_2}_{m_2}[/math] = expansion of the systems total angular momentum in terms of the uncoupled original basis states of each individual constituent

[math]\Psi^{3/2}_{3/2} = \sum_{m_1,m_2} C^{1,1/2,3/2}_{m_1,m_2,3/2} \psi^{1}_{m_1} \psi^{1/2}_{m_2} = C^{1,\frac{1}{2},\frac{3}{2}}_{1,\frac{1}{2},\frac{3}{2}}\psi^{1}_{1} \psi^{1/2}_{1/2} [/math] : all other possible m_1 and m_2 values don't add to M

[math]\Psi^{3/2}_{1/2} = \sum_{m_1,m_2} C^{1,1/2,3/2}_{m_1,m_2,1/2} \psi^{1}_{m_1} \psi^{1/2}_{m_2} = C^{1,\frac{1}{2},\frac{3}{2}}_{0,\frac{1}{2},\frac{1}{2}}\psi^{1}_{0} \psi^{1/2}_{1/2} + C^{1,\frac{1}{2},\frac{3}{2}}_{1,\frac{-1}{2},\frac{1}{2}}\psi^{1}_{1} \psi^{1/2}_{-1/2}[/math] : all other possible m_1 and m_2 values don't add to M

If I constrain the helicity of my virtual photon to be +1 by preparing electrons with spins along their direction of motion, then the state [math]\psi^{1}_{0}[/math] doesn't exist so only only one state enters the sum

[math]\Psi^{3/2}_{1/2} = C^{1,\frac{1}{2},\frac{3}{2}}_{1,\frac{-1}{2},\frac{1}{2}}\psi^{1}_{1} \psi^{1/2}_{-1/2}[/math] : all other possible m_1 and m_2 values don't add to M

[math]C^{j_1,j_2,J}_{m_1,m_2,M}[/math] : Clebsch-Gordon Coefficient [math]C^{1,\frac{1}{2},\frac{3}{2}}_{1,\frac{1}{2},\frac{3}{2}}=1[/math] [math]C^{1,\;\;\frac{1}{2},\frac{3}{2}}_{1,-\frac{1}{2},\frac{1}{2}}= \frac{1}{\sqrt{3}}[/math]

[math]A = \frac{\sigma_{\frac{1}{2}} - \sigma_{\frac{3}{2}}}{\sigma_{\frac{1}{2}} + \sigma_{\frac{3}{2}}} = \frac{\frac{1}{3} - 1}{\frac{1}{3} + 1} = -1/2[/math]

Quark Distributions

[math]\sigma_p^{\pi^+ \pm \pi^-} = \frac{1}{9}[4( u + \bar{u}) \pm ( d + \bar{d})]D_u^{\pi^+ \pm \pi^-}[/math]

[math]\sigma_n^{\pi^+ \pm \pi^-} = \frac{1}{9}[4(d + \bar{d}) \pm (u + \bar{u})]D_u^{\pi^+ \pm \pi^-}[/math]

[math]\sigma_{2H}^{\pi^+ \pm \pi^-} = \frac{5}{9}[( u + \bar{u}) \pm ( d + \bar{d})]D_u^{\pi^+ \pm \pi^-}[/math]

The polarized distributions may be expressed in a similar fashion:

[math]\sigma_{\frac{1}{2}}[/math](Struck quark spin is [math]\parallel[/math] to Nucleon spin)	[math]\sigma_{\frac{3}{2}}[/math] (Struck quark spin is [math]\not\parallel[/math] to Nucleon spin)

[math]\frac{d^3 \sigma^h_{1/2}}{dxdQ^2 dz}\approx \Sigma_q e_q^2 q^{\parallel}(x,Q^2)D_q^h(z,Q^2)[/math]

[math]\frac{d^3 \sigma^h_{3/2}}{dxdQ^2 dz}\approx \Sigma_q e_q^2 q^{\not\parallel}(x,Q^2)D_q^h(z,Q^2)[/math]

[math]\frac{d^3 \sigma^h_{1/2(3/2)}}{dxdQ^2 dz}\approx \Sigma_q e_q^2 q^{+(-)}(x,Q^2)D_q^h(z,Q^2)[/math]

[math]\Delta \sigma_p^{\pi^+ \pm \pi^-} = \frac{1}{9}[4(\Delta u + \Delta \bar{u}) \pm (\Delta d + \Delta \bar{d})]D_u^{\pi^+ \pm \pi^-}[/math]

[math]\Delta \sigma_n^{\pi^+ \pm \pi^-} = \frac{1}{9}[4(\Delta d + \Delta d^-) \pm (\Delta u + \Delta u^-)]D_u^{\pi^+ \pm \pi^-}[/math]

[math]\Delta \sigma_{2H}^{\pi^+ \pm \pi^-} = \frac{5}{9}[(\Delta u + \Delta \bar{u}) \pm (\Delta d + \Delta \bar{d})]D_u^{\pi^+ \pm \pi^-}[/math]

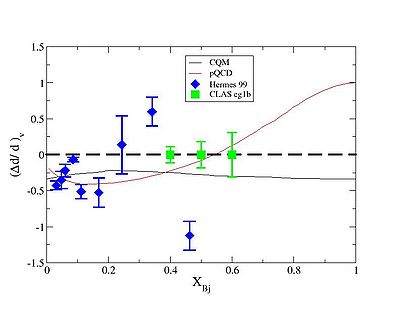
Delta d-over d

[math]X_{Bj}[/math] vs [math]\frac{\Delta d_v}{d_v}[/math]

References

Past colloquia

TF_01092012_Colloq

Theory

Phenomenological

NP, B291(1987)793; NP, B346(1990)1;

    Z. Phys. C56(1992)493;
    Eur. Phys. J. C44  (2005)219;
    hep-ph/0205123
    arXiV:1310.5285

QCD inspired

NP, B483(1997)291; NP, B484(1997)265;

    PRL 85(2000)3591; PRL 89(2002)162301;
    JHEP 0211(2002)44; NP, A720(2003)131; 
    Eur. Phys. J. C30(2003)213; arXiV:09073534;
    NP, A761(2005)67; PR, C81(2010)024902

Hybrids

PYTHIA + BUU simulation

     PR, C70(2004)054609; NP, A801(2008)68

Experiment

keith's 2012 talk in Italy on EG1-DVCS

Unpolarized

http://link.springer.com/article/10.1007%2FJHEP04%282014%29005

File:AndyMiller 200TalkAtDESY.pdf 2002 talk by CA Miller at DESY

File:Dueren.98.055.pdf 1998 Duren talk

2013 APS talk on EG1-DVCS

July 30,2014 talk by XingLong Li at Heremes File:XingLongLi TalkOnPACIAEmdoelForSIDIS.pdf from

http://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=31&ved=0CB0QFjAAOB4&url=http%3A%2F%2Fhadron2014.csp.escience.cn%2Fdct%2Fattach%2FY2xiOmNsYjpwZGY6MzAwMjA%3D&ei=UPw1VNiQAdHlsATA7IHwDw&usg=AFQjCNH5yyek_zTJ22TZq0Dw_YLUeAxe2Q

Xiangs proposal for CLAS12 measurement of SIDIS Xsections see Fig. 1

Semi-inclusive deep inelastic scattering at small transverse momentum

Naomi's SIDIS Hermes talk from 2011 at NNPSS11

1986 article ob QCD effects in semi-inclusive deep inelastic scattering from a polarized target by P. Chiappetta J. -Ph. Guillet

theses

2014 Ph.D thesis of Naomi's student Sylvester Joosten

http://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=7&cad=rja&uact=8&ved=0CFYQFjAG&url=http%3A%2F%2Fwww.nikhef.nl%2Fpub%2Fservices%2Fbiblio%2Ftheses_pdf%2Fthesis_E_Garutti.pdf&ei=Osw3VJbSAY27ogSx3IDwDQ&usg=AFQjCNENlNdgPr6dgfq9OanlL8cUnYHmMQ&bvm=bv.77161500,d.cGU

TF_SIDIS_Physics