Difference between revisions of "Sadiq Thesis"
| Line 235: | Line 235: | ||
<math> | <math> | ||
| − | |||
\centering | \centering | ||
\caption{Emittance Measurement Results.} | \caption{Emittance Measurement Results.} | ||
| Line 258: | Line 257: | ||
\end{tabular} | \end{tabular} | ||
\label{results} | \label{results} | ||
| − | |||
</math> | </math> | ||
Revision as of 00:49, 11 February 2013
Introduction
Positron
Positron is the antimatter of electron. Positrons have same mass as electron ( ), carries positive charge, and it is noted as "".
Positrons predicted by Paul Dirac in 1928, <ref name="Dirac1928"> The Quantum Theory of the Electron, P. A. M. Dirac, Proc. R. Soc. Lond. A February 1, 1928 117 778 610-624;</ref>, and experimentally observed by Dmitri Skobeltsyn in 1929 and by Carl D. Anderson in 1932 <ref name="e+_discover"> General Chemistry, Taylor and Francis. p. 660. </ref>. Anderson also coined the term positron and he won the Nobel Prize for Physics in 1936.
<ref name="name"> BOOK_Gernal, Auther, Month_Year,issue,page </ref>
Positron Beamline History
Theory
positron creation from Bremsstrahlung
Positron rate prediction
Apparatus
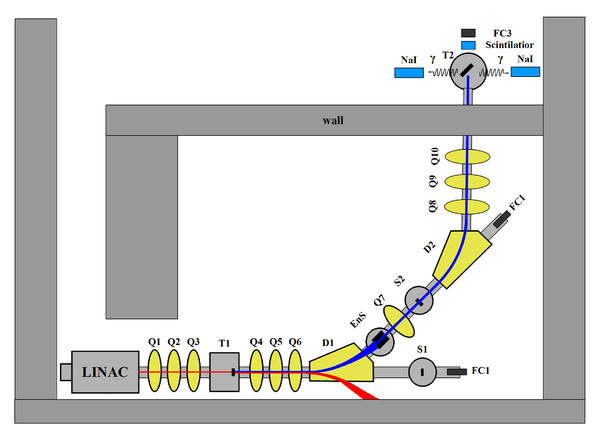
HRRL Positron Beamline
HRRL beamline layout is given in the figure below, and the item descriptions are given in the table below.
| Item | Description |
| T1 | Positron target |
| T2 | Annihilation target |
| EnS | Energy Slit |
| FC1, FC2 | Faraday Cups |
| Q1,...Q10 | Quadrupoles |
| D1, D2 | Dipoles |
| NaI | NaI Detecotrs |
| OTR | Optical Transition Radiaiton screen |
| YAG | Yttrium Aluminium Garnet screen |
Som parameters of HRRL is given by:
| Parameter | Unit | Value |
| maximum energy | MeV | 16 |
| peak current | mA | 100 |
| repetition rate | Hz | 300 |
| absolute energy spread | MeV | 2-4 |
| macro pulse length | ns | >50
|
Beam properties
Emittance Measurement
Emittance is an important parameter in accelerator physics. If emittance with twiss parameters are given at the exit of the gun, we will be able to calculate beam size and divergence any point after the exit of the gun. Knowing the beam size and beam divergence on the positron target will greatly help us study the process of creating positron. Emittance with twiss parameters are also key parameters for any accelerator simulations. Also, energy and energy spread of the beam will be measured in the emittance measurement.
What is Emittance
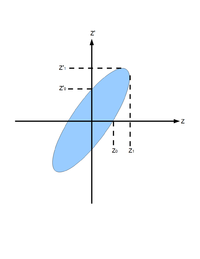
In accelerator physics, Cartesian coordinate system was used to describe motion of the accelerated particles. Usually the z-axis of Cartesian coordinate system is set to be along the electron beam line as longitudinal beam direction. X-axis is set to be horizontal and perpendicular to the longitudinal direction, as one of the transverse beam direction. Y-axis is set to be vertical and perpendicular to the longitudinal direction, as another transverse beam direction.
For the convenience of representation, we use to represent our transverse coordinates, while discussing emittance. And we would like to express longitudinal beam direction with . Our transverse beam profile changes along the beam line, it makes is function of , . The angle of a accelerated charge regarding the designed orbit can be defined as:
If we plot vs. , we will get an ellipse. The area of the ellipse is an invariant, which is called Courant-Snyder invariant. The transverse emittance of the beam is defined to be the area of the ellipse, which contains 90% of the particles <ref name="MConte08"> M. Conte and W. W. MacKay, “An Introduction To The Physics Of Particle Accelera tors”, World Scientifc, Singapore, 2008, 2nd Edition, pp. 257-330. </ref>.
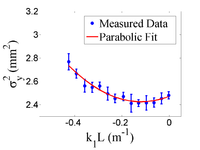
By changing quadrupole magnetic field strength , we can change beam sizes on the screen. We make projection to the x, y axes, then fit them with Gaussian fittings to extract rms beam sizes, then plot vs vs . By Fitting a parabola we can find constants ,, and , and get emittances.
Emittance Measurements with an OTR
A beam emittance measurement of the HRRL was performed at Idaho State University's IAC with YAG (Yttrium Aluminium Garnet) was performed. Due to the high sensitivity of YAG, the beam image was saturated and beam spot pears rather big. Comparison study shows that for same beam YAG screen shows bigger beam size than Optical Transition Radiation (OTR) screen. An OTR based viewer was installed to allow measurements at the high electron currents available using the HRRL.
The OTR screen is 10 thick aluminium. Beam images were taken with digital CCD camera, a MATLAB tool were used to extract beamsize and emittance.
The visible light from the OTR based viewer is produced when a relativistic electron beam crosses the boundary of two mediums with different dielectric constants. Visible radiation is emitted at an angle of 90 degree with respect to the incident beam direction<ref name="OTR"> Tech. Rep., B. Gitter, Los Angeles, USA (1992). </ref> when the electron beam intersects the OTR target at a 45 degree angle. These backward-emitted photons are observed using a digital camera and can be used to measure the shape and intensity of the electron beam based on the OTR distribution.
Quadrupole Scanning Method
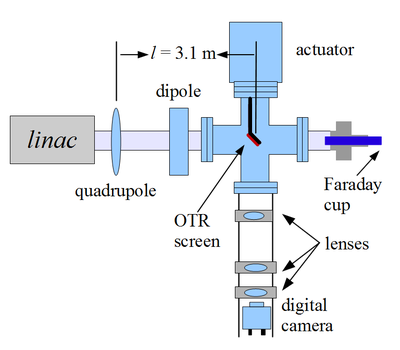
Fig. on the right illustrates the apparatus used to measure the emittance using the quadrupole scanning method. A quadrupole is positioned at the exit of the linac to focus or de-focus the beam as observed on a downstream view screen. The 3.1 m distance between the quadrupole and the screen was chosen in order to minimize chromatic effects and to satisfy the thin lens approximation.
Assuming the thin lens approximation, , is satisfied, the transfer matrix of a quadrupole magnet may be expressed as
where is the quadrupole strength, is the length of quadrupole, and is the focal length. A matrix representing the drift space between the quadrupole and screen is given by
where is the distance between the scanning quadrupole and the screen. The transfer matrix of the scanning region is given by the matrix product . In the horizontal plane, the beam matrix at the screen () is related to the beam matrix of the quadrupole () using the similarity transformation
where the and are defined as <ref name="SYLee"> Accelerator Physics, S.Y. Lee, (Singapore: World Scientific, 2004), 61. </ref>
By defining the new parameters <ref name="quad-scan"> D.F.G. Benedetti, et al., Tech. Rep., DAFNE Tech. Not., Frascati, Italy (2005). </ref>,
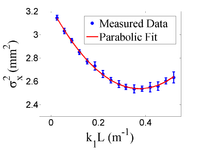
the matrix element , the square of the rms beam size at the screen, may be expressed as a parabolic function of the product of and
The emittance measurement was performed by changing the quadrupole current, which changes , and measuring the corresponding beam image on the view screen. The measured two-dimensional beam image was projected along the image's abscissa and ordinate axes. A Gaussian fitting function is used on each projection to determine the rms value, in Eq.~(\ref{par_fit}). Measurements of for several quadrupole currents () is then fit using the parabolic function in Eq.~(\ref{par_fit}) to determine the constants , , and . The emittance () and the Twiss parameters ( and ) can be found using Eq.~(\ref{emit-relation}).
The OTR Imaging System
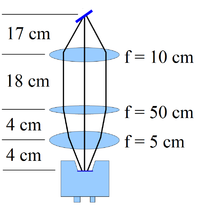
The OTR target is 10 m thick aluminum foil with a 1.25 inch diameter. The OTR is emitted in a cone shape with the maximum intensity at an angle of with respect to the reflecting angle of the electron beam<ref name="OTR"></ref>. Three lenses, 2 inches in diameter, are used for the imaging system to avoid optical distortion at lower electron energies. The focal lengths and position of the lenses are shown in Fig. on the right. The camera used was a JAI CV-A10GE digital camera with a 767 by 576 pixel area. The camera images were taken by triggering the camera synchronously with the electron gun.
Quadrupole Scanning
The quadrupole current is changed to alter the strength and direction of the quadrupole magnetic field such that a measurable change in the beam shape is seen by the OTR system. Initially, the beam was steered by the quadrupole indicating that the beam was not entering along the quadrupole's central axis. Several magnetic elements upstream of this quadrupole were adjusted to align the incident electron beam with the quadrupole's central axis. First, the beam current observed by a Faraday cup located at the end of beam line was maximized using upstream steering coils within the linac nearest the gun. Second, the first solenoid nearest the linac gun was used to focus the electron beam on the OTR screen. Steering coils were adjusted to maximize the beam current to the Faraday cup and minimize the deflection of the beam by the solenoid first then by the quadrupole. A second solenoid and the last steering magnet, both near the exit of the linac, were used in the final step to optimize the beam spot size on the OTR target and maximize the Faraday cup current. A configuration was found that minimized the electron beam deflection when the quadrupole current was altered during the emittance measurements.
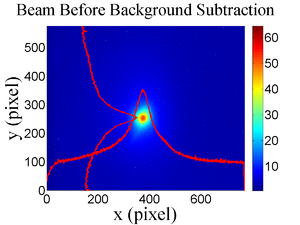
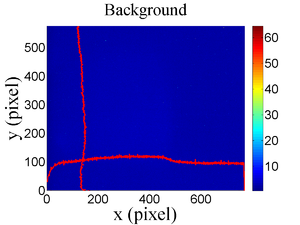
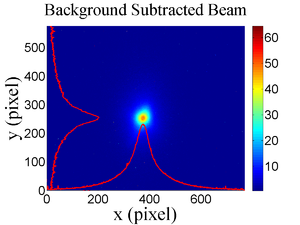
The emittance measurement was performed using an electron beam energy of 15~MeV and a 200~ns long, 40~mA, macro pulse peak current. The current in the first quadrupole after the exit of the linac was changed from $-$~5~A to 5~A with an increment of 0.2~A. Seven measurements were taken at each current step in order to determine the average beam width and the variance. Background measurements were taken by turning the linac's electron gun off while keep the RF on. Background image and beam images before and after background subtraction are shown in Fig.~\ref{bg}. A small dark current is visible in Fig.~\ref{bg}b that is known to be generated when electrons are pulled off the cavity wall and accelerated.
In Fig. below, the images of the electron shown for 0, +1 and +2 Q1 coildcurrents.
The electron beam energy was measured using a dipole magnet downstream of the quadrupole used for the emittance measurements. Prior to energizing the dipole, the electron micro-pulse bunch charge passing through the dipole was measured using a Faraday cup located approximately 50~cm downstream of the OTR screen. The dipole current was adjusted until a maximum beam current was observed on another Faraday cup located just after the 45 degree exit port of the dipole. A magnetic field map of the dipole suggests that the electron beam energy was 15~~1.6~MeV. Future emittance measurements are planned to cover the entire energy range of the linac.
Data Analysis and Results
Images from the JAI camera were calibrated using the OTR target frame. An LED was used to illuminate the OTR aluminum frame that has a known inner diameter of 31.75~mm. Image processing software was used to inscribe a circle on the image to measure the circular OTR inner frame in units of pixels. The scaling factor can be obtained by dividing this length with the number of pixels observed. The result is a horizontal scaling factor of 0.04327~~0.00016~mm/pixel and vertical scaling factor of 0.04204~~0.00018~mm/pixel. Digital images from the JAI camera were extracted in a matrix format in order to take projections on both axes and perform a Gaussian fit. The observed image profiles were not well described by a single Gaussian distribution. The profiles may be described using a Lorentzian distribution, however, the rms of the Lorentzian function is not defined. The super Gaussian distribution seems to be the best option~\cite{sup-Gau}, because rms values may be directly extracted.
Fig.~\ref{par-fit} shows the square of the rms () vs k_1L for x (horizontal) and y (vertical) beam projections along with the parabolic fits using Eq.~\ref{par_fit}. The emittances and Twiss parameters from these fits are summarized in Table~\ref{results}. An automatic MATLAB based emittance measurement tool is under development~\cite{emit-mat}.
<ref name="emit-mat"> C.F. Eckman et al., in Proc. IPAC2012, New Orleans, USA. </ref>. I used the MATLAB to analyze the data. The results shows that:
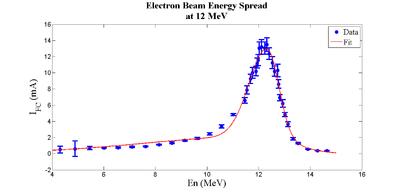
Energy Spread Measurement
Energy scan was done to measure the energy profile of HRRL at nominal 12 MeV. A Faraday cup was placed at the end of the 45 degree beamline to measure the electron beam current bent by the first dipole. Dipole coil current were changed by 1 A increment and the Faraday cup currents were recorded. The scan results with corresponding beam energies are shown in the table below.
The energy distribution of HRRL can be described by two skewed Gaussian fit overlapping.
Dipole FC En Coil Current Current Reading (A) (mA) (MeV) 8 0.5 4.3119 9 0.6 4.8896 10 0.67 5.4570 11 0.716 6.0141 12 0.752 6.5610 13 0.828 7.0975 14 0.896 7.6238 15 1.112 8.1399 16 1.328 8.6456 17 1.624 9.1411 18 1.896 9.6262 19 2.448 10.1012 20 3.36 10.5658 21 4.82 11.0201 22 6.58 11.4642 22.2 7.88 11.5518 22.5 9.24 11.6824 22.7 10.0 11.7690 23 10.2 11.8980 23.1 11.2 11.9408 23.2 11.56 11.9836 23.3 13.04 12.0262 23.5 13.2 12.1111 23.8 13.04 12.2377 24 13.48 12.3216 24.2 12.36 12.4050 24.5 11.24 12.5295 24.7 10.2 12.6119 25 10.28 12.7348 25.1 8.6 12.7756 25.2 6.92 12.8162 25.5 6.2 12.9376 25.7 4.84 13.0180 26 3.64 13.1378 26.5 1.82 13.3354 27 1.28 13.5305 28 0.56 13.9129 29 0.364 14.2850 30 0.364 14.6469
2 Skewed Gaussian Fit
Beam Distributions Beyond RMS: Media:Beam_Distributions_Beyond_RMS.pdf
Amplitude = 2.13894, mean = 12.07181, sigma_L = 4.46986, sigma_R = 1.20046
Sigma = 2.83516, Es = -0.57658
rms = 2.56472, skew = -0.94853
Amplitude2 = 10.88318, mean2 = 12.32332, sigma_L2 = 0.69709, sigma_R2 = 0.45170
Sigma2 = 0.57440, Es2 = -0.21360
rms2 = 0.56719, skew2 = -0.34231
Current, rep-rate
Radiation Footprint
Positron detection
DAQ setup
Trigger for DAQ
NaI detector dynode signal amplified and delayed to initiate trigger logic. Then
Data Analysis
Signal extraction
For 3 MeV and on detector show all the steps
- Raw counts target in and out (calibrated energy)
- Normalized counts
- background subtracted
- Integral (zoomed in and with error)
Example of error propagation for the above
Raw counts target in and out
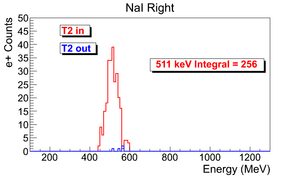
Lets take example of run#3735 for the data analysis.
The ingeral shown in read is from the background is subtracted spectrum.
| run in: 3735 | run out: 3737 | 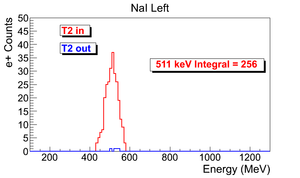
|
|
Some run parameters in 3735:
| run number | Reprate | Run time | Pulses | Events | e+ Counts NaI Detectors |
| 3735 | 300 Hz | 1002 s | 301462 | 9045 | 256 +- 16 |
Electron Rate Calculation
A scintillator placed between quadrupole 9 and quarupole 10 (shown as in the following figures) was used to estimate electron current:
Scintillator Charge Calbiration
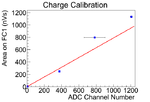
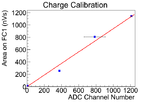
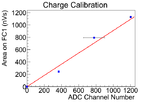
The electron beam current was changed to calibrate of the scintillator. The mean of the counts in scintillator decreased in the experiment as the current decreased, the change is linear.
The data was fitted with three methods to find calbiration, and the average and variance them are used to find the calibration.
The first method is fit the three data points with root.
The second method, the point (0,0) introduced, and the line was forced to pass through this point. The point is introduced based on physics that when there is no electron beam, scintillator should have no counts. The slope was fitted by root. The fit is done in root.
In the second method, the curved is far off from the two data points when ADC channel number is large. The third fitting method is introduced to compensate it, in which fits are done manually. Two fits were done by this method, and average and variance of two fits were obtained.
The average and variance of these three methods were used for the calibration of the scintillator.
| Fit Methods | Fit Method 1 | Fit Method 2 | Fit Method 3 | Average of Three Methods |
| Fit Curve | 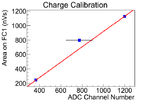
|
|
  |
|
| Calibration | nV s /ADC channel | nV s /ADC channel | nV s /ADC channel | nV s /ADC channel |
Electron Current Calculation for Run 3735
Total number of electrons in this run
Total charge of electrons in this run:
Electron rate:
Average electron current:
Positron Rate Calculation
This a normalized spectrum (no background subtraction).
| run in: 3735 | 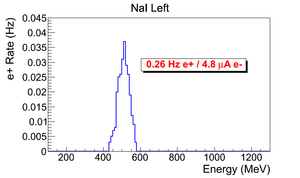
|
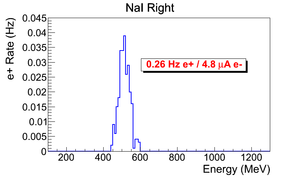
|
positron rate:
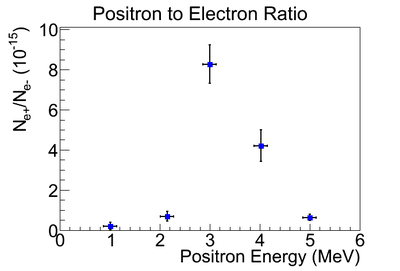
Positron to Electron Ratio
positron to electron ratio:
positron to electron current ratio:
Hand Calculation of Errors
Background subraction
| Run Number | T2 Position | |
| 3735 | in | |
| 3736 | out | |
| 3737 | in |
All Energies
Sources of Systematic Errors
Efficiency measurement
acceptance, quad collection efficiency,
Conclusion
References
<references/>