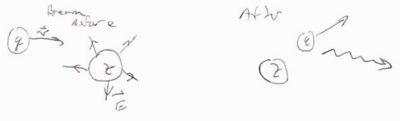|
|
| Line 35: |
Line 35: |
| | | | |
| | Ann. Phys. vol. 5, 325, (1930) | | Ann. Phys. vol. 5, 325, (1930) |
| − |
| |
| − | === Energy Straggling ===
| |
| − |
| |
| − | While the Bethe-Bloch formula gives you a way to quantify the amount of energy a heavy charged particle loses as a function of the distance traveled, you should realize that when you calculate the total energy lost via
| |
| − |
| |
| − | :<math> \Delta E = \int_{E_i}^{E_f} \left ( \frac{dE}{dx} \right ) dx</math>
| |
| − |
| |
| − | you are only determining the AVERAGE energy loss. In other words, Bethe-Bloch is the Astochastic process describing energy loss.
| |
| − |
| |
| − | In reality the energy loss process is a stochastic process because of the statistical fluctuations which occur in the actual number of collisions which take place.
| |
| − |
| |
| − |
| |
| − | ==== Thick Absorber ====
| |
| − |
| |
| − | A thick absorber is one in which a large number of collisions takes place. In this situation the central limit theorem from statistics tells you that the larger number of random variables <math>N</math> involved will result in observables which are distributed in a Gaussian manner. The Gaussian distribution is a good approximation to the binomial distribution when the number of trials is large.
| |
| − |
| |
| − | [[Forest_ErrAna_StatDist#Binomial_with_Large_N_becomes_Gaussian]]
| |
| − |
| |
| − | , and to a Poisson distribution when the mean is a lot larger than 1.
| |
| − |
| |
| − | [[Forest_ErrAna_StatDist#Gaussian_approximation_to_Poisson_when]]
| |
| − |
| |
| − | The gaussian probability function is defined as
| |
| − |
| |
| − | : <math>P(x,\Delta) \propto e^{\frac{(\Delta - \bar{\Delta})^2}{ \sigma^2}}</math>
| |
| − |
| |
| − | where the Full Width at Half Max (FWHM) of the distribution = <math>\left ( 2 \sqrt{2 \ln 2} \right ) \sigma</math>
| |
| − |
| |
| − | In the case of energy loss, the variance using the Bethe-Bloch equation should be
| |
| − |
| |
| − | :<math>\sigma_0^2 = 4 \pi N r_e^2 (m_e c^2)^2 \rho \frac{Z}{A} x</math>
| |
| − |
| |
| − | the realitivistic variance is
| |
| − |
| |
| − | : <math>\sigma^2 = [\frac{1-\beta^2/2}{1-\beta^2} ]\sigma_0^2</math>
| |
| − |
| |
| − | for very thick absorbers see
| |
| − |
| |
| − | C. Tschaler, NIM '''64''', (1968) 237 ; ''ibid'', '''61''', (1968) 141
| |
| − |
| |
| − | When simulating energy loss of heavy charged particles the Bethe-Bloch equation may be used to calculate a <math>\frac{dE}{dx}</math> which can determine the average energy loss at the given kinetic energy of the particle. This average is then smeared according to a gaussian distribution of variance
| |
| − |
| |
| − | : <math>\sigma^2 =4 \pi N r_e^2 (m_e c^2)^2 \rho \frac{Z}{A} x [\frac{1-\beta^2/2}{1-\beta^2} ]</math>
| |
| − |
| |
| − | ====Thin Absorbers====
| |
| − |
| |
| − | In thin absorbers the number of collisions is small preventing the use of the central limit theorem to describe the stochastic process of energy loss in terms of a Gaussian distribution. The large energy transfers that are possible cause the energy loss distribution to look like a Gaussian with a high energy tail (or foot).
| |
| − |
| |
| − | The skewness of the resulting energy loss distribution is quantified as
| |
| − |
| |
| − | :<math>\kappa = \frac{\bar{\Delta}}{W_{max}}</math>
| |
| − |
| |
| − | : <math>\Delta \equiv 2 \pi N_a r_e^2 m_e c^2 \rho \frac{Z}{A} \left ( \frac{z}{\beta}\right)^2 x </math> = lead term in Bethe Bloch equation
| |
| − |
| |
| − | <math>\rho</math> = density of absorbing material.
| |
| − |
| |
| − | :<math>W_{max} = \frac{(pc)^2}{\frac{1}{2} \left [ m_e c^2 + \left ( \frac{M^2 c^2}{m_e} \right ) \right ] + \sqrt{(pc)^2 + (Mc^2)^2}}</math> = max energy transfered in 1 collision (headon / knock out collision)
| |
| − |
| |
| − | This comes from the relativistic kinematics of an Elastic Collision.<br>
| |
| − | [[Image:SPIM_ThinAbsorbers_Scatering.jpg | 400 px]]
| |
| − |
| |
| − | : <math>\gamma = \frac{E_{tot}}{Mc^2} = \frac{ \sqrt{(pc)^2 + (Mc^2)^2}}{Mc^2}</math>
| |
| − | :<math>\beta= \frac{pc}{\gamma Mc^2} = \frac{pc}{E_{tot}}</math>
| |
| − | : <math>E_k = E_{tot} - Mc^2 = \gamma Mc^2 - Mc^2 = (\gamma - 1 ) Mc^2</math>
| |
| − | : <math>E_k = \sqrt{(pc)^2 + (Mc^2)^2} - Mc^2 </math>
| |
| − | :<math> (p^{\prime}c)^2 = E_k^2 + 2E_km_ec^2</math>
| |
| − |
| |
| − |
| |
| − | Conservation of Momentum <math>\Rightarrow</math> :
| |
| − |
| |
| − | : <math>\vec{p} = \vec{p}^{\; \prime \prime} + \vec{p}^{\; \prime}</math>
| |
| − |
| |
| − | Conservation of Energy <math>\Rightarrow</math> :
| |
| − |
| |
| − | : <math>E_{tot} + m_ec^2 = E_{tot}^{\prime \prime} + E_{tot}^{\prime}</math>
| |
| − | : <math>\sqrt{(pc)^2 + (Mc^2)^2} + m_ec^2 = \sqrt{(p^{\; \prime \prime} c)^2 + (Mc^2)^2} + E_k + m_e c^2</math>
| |
| − |
| |
| − |
| |
| − | using conservation of E & P as well as substituting for <math>p^{\prime}</math> you can show
| |
| − |
| |
| − | :<math>(p^{\; \prime \prime}c)^2 = (pc)^2 - 2E_k\sqrt{(pc)^2 +(Mc^2)^2} + E_k^2</math> : cons of E
| |
| − | :<math>= (pc)^2 + E_k^2 + 2E_km_ec^2 -2pc\sqrt{E_k^2+2E_km_ec^2} \cos(\theta)</math> : cons of P
| |
| − |
| |
| − | <math>\Rightarrow</math>
| |
| − |
| |
| − | : <math>pc \cos(\theta) \sqrt{1+\frac{2m_ec^2}{E_k}} = \sqrt{(pc)^2+(Mc^2)^2} + m_ec^2</math>
| |
| − |
| |
| − | solving for <math>E_k</math>
| |
| − |
| |
| − | :<math>E_k = \frac{2m_ec^2(pc)^2\cos^2 (\theta)}{[\sqrt{(pc)^2 + (Mc^2)^2} +m_ec^2]^2 - (pc)^2 \cos^2 (\theta)}</math>
| |
| − |
| |
| − | ===== (Landau Theory) =====
| |
| − | <math>\kappa \leq 0.01</math>
| |
| − |
| |
| − | Landau assumed
| |
| − | :# <math>W_{max} = \infty</math> is max energy transfer
| |
| − | :# electrons are free (energy transfer is so large you can neglect binding)
| |
| − | :# incident particle maintains velocity (large momentum transfer from big mass to small mass) (bowling ball hits ping pong ball)
| |
| − |
| |
| − | L. Landau, "On the Energy Loss of Fast Particles by Ionization", J. Phys., vol 8 (1944), pg 201
| |
| − |
| |
| − | instead of a gaussian distribution Landau used
| |
| − |
| |
| − | : <math>P(x,\Delta) \propto \frac{1}{\bar{\Delta}\pi} \int_0^{\infty} e^{-u \ln u - u \lambda} \sin(\pi u) du</math>
| |
| − |
| |
| − | where
| |
| − |
| |
| − | : <math>\lambda = \frac{1}{\bar{\Delta}} \left [ \Delta - \bar{\Delta} \ln \bar{\Delta} - \ln \epsilon + 1 -C \right ]</math>
| |
| − | : <math>\bar{\Delta} = 2\pi N_a r_e^2 m_e c^2 \rho \frac{Zz^2}{A \beta^2}x</math>
| |
| − | :<math>\ln \epsilon = \ln \left [ \frac{(1-\beta^2)I^2}{2m_ec^2 \beta^2} \right ]</math>
| |
| − | : <math>C = 0.577</math>
| |
| − |
| |
| − | [[Image:SPIM_Landau_ThinAbsorberDist.jpg]]
| |
| − |
| |
| − | ===== (Vavilou's Theory) =====
| |
| − |
| |
| − | Vavilous paper
| |
| − |
| |
| − | P.V. Vavilou, "Ionization losses of High Energy Heavy Particles", Soviet Physics JETP, vol 5 (1950? )pg 749
| |
| − |
| |
| − | describe the physics for the case
| |
| − |
| |
| − | ;<math>0.01 < \kappa < \infty </math>
| |
| − |
| |
| − | The distribution function derived is shown below as well as a conceptual overlay of Vavilou's and Landau's distributions. (The <math>\zeta f(x,\Delta)</math> in the picture should be a <math>\bar{\Delta}P(x,\Delta)</math> )
| |
| − |
| |
| − |
| |
| − | : <math>P(x,\Delta) = \frac{1}{\bar{\Delta}\pi} x e^{x(1+\beta^2C)} \int_0^{\infty} e^{xf_1} \cos(y \lambda_1 + xf_2) dy</math>
| |
| − |
| |
| − | where
| |
| − |
| |
| − | : <math>f_1 = \beta^2 \left [ \ln(y) - C_i(y)\right ] - \cos(y) - y S_i(y)</math>
| |
| − | : <math>f_2 = y\left [ \ln(y) - C_i(y)\right ] + \sin(y) + \beta^2 S_i(y)</math>
| |
| − | : <math>C_i(y) \equiv - \int_y^{\infty} \frac{\cos(t)}{t} dt</math>
| |
| − | : <math>S_i(y) \equiv \int_0^{y} \frac{\sin(t)}{t} dt</math>
| |
| − | : <math>C = 0.577</math>
| |
| − |
| |
| − | [[Image:SPIM_Vavilou_Landau_ThinAbsorber.jpg | 400 px]]
| |
| − |
| |
| − | ==== GEANT4's implementation ====
| |
| − |
| |
| − | GEANT 4 uses the skewness parameter <math>\kappa</math> to determine if it will use a "fluctuations model" to calculate energy straggling or the gaussian model described in section 3.2.1.
| |
| − |
| |
| − | ===== kappa > 10 =====
| |
| − | If
| |
| − | : <math>\kappa \equiv \frac{ \bar{\Delta}}{W_{max}}</math> > 10
| |
| − | and we have a thick absorber ( large step size) then the Gausian function in 3.2.1 is used to calculate energy straggling.
| |
| − |
| |
| − | What happens is <math>\Delta E</math> is calculated via <math>\int_{E_i}^{E_f} \frac{dE}{dx} dx</math> then the actual energy loss predicted by the simulation is chosen from a Gaussian distribution to account for energy straggling such that the <math>\sigma</math> of this Gaussian distribution is given by:
| |
| − |
| |
| − | :<math>\sigma^2 = 2 \pi r_e^2m_ec^2N_{el} \frac{Z_h}{\beta^2} T_C s (1 - \frac{\beta^2}{2})</math>
| |
| − |
| |
| − | where
| |
| − |
| |
| − | :<math>N_{el}</math> = electron density of the medium
| |
| − | :<math>Z_h</math> = charge of the incident particle
| |
| − | :<math>s</math> = step size
| |
| − | :<math> T_C</math> = cutoff kinetic energy for <math>\delta </math>-electrons
| |
| − |
| |
| − | <math>T_C</math> tells GEANT where to put the cutoff for using the Gaussian distribution for energy straggling. This tells the simulation the low energy cutoff where Bethe-Bloch starts to fail due to ionization.
| |
| − |
| |
| − | =====Delta-electrons =====
| |
| − | What is a <math>\delta</math> - electron?
| |
| − |
| |
| − | <math>\delta</math> - electrons are also known as "knock -on" electrons and delta rays.
| |
| − |
| |
| − | As heavy particles traverse a medium they can ionize electrons from atoms. The ejected electrons can be given enough energy to ionize as well.
| |
| − |
| |
| − | In a cloud chamber (a supercooled volume of super saturated water vapor which ionizes as charged particles pass through) such and event would look like:
| |
| − |
| |
| − | [[Image:SPIM_DeltaRay_CloudChamber.jpg | 400 px]]
| |
| − |
| |
| − | The blue spiral in the above gas chamber picture is a high energy electron from the collision. The B-field is directed out of the picture.
| |
| − |
| |
| − | The physics of ionization is different from the physics used to calculate Bethe-Bloch energy loss. Remember Bethe-Bloch starts to break down at low energies below the Bragg peak.
| |
| − |
| |
| − | Because of this GEANT 4 sets the cutoff for this process to be
| |
| − |
| |
| − | : <math>T_{cut}</math> > 1 keV
| |
| − |
| |
| − |
| |
| − | Note: The BE energies of an electron in Hydrogen is 13.6 ev and the electrons in Argon have binding energies between 15.7 eV and 3.2 keV.
| |
| − |
| |
| − | ===== Fluctuations Model: kappa < 10=====
| |
| − |
| |
| − | If <math>\kappa \equiv \frac{ \bar{\Delta}}{W_{max}} < \frac{\Delta E}{T_C}</math>
| |
| − |
| |
| − | Then GEANT 4 uses a "Fluctuations Model" to determine energy loss instead of Bethe-Bloch.
| |
| − |
| |
| − | ; Fluctuations Model
| |
| − | :# the atom is assumed to have on 2 energy levels <math>E_1</math> and <math>E_2</math>
| |
| − | :# you can excite the atom and lose either <math>E_1</math> or <math>E_2</math> or you can ionize the atom and lose energy according to a <math>\frac{1}{E^2}</math> function <math>u_j</math>.
| |
| − |
| |
| − | The total energy loss in a step will be
| |
| − |
| |
| − | : <math>\Delta E = \Delta E_{exc} + \Delta E_{ion}</math>
| |
| − |
| |
| − | where
| |
| − |
| |
| − | : <math>\Delta E_{exc} = \eta_1 E_1 + \eta_2 E_2</math>
| |
| − |
| |
| − | : <math>\Delta E_{ion} = \sum_{j=1}^{\eta_3} \frac{I}{1 - u_j \frac{T_{up}-I}{T_{up}}}</math>
| |
| − |
| |
| − | :<math>\eta_1</math>, <math>\eta_2</math>, and <math>\eta_3</math> are the number of collisions which are sampled from a poison distribution
| |
| − |
| |
| − | :<math>u_j = \int_{I}^{E_j} \frac{I T_{up}}{T_{up} - I} \frac{dx}{x^2}</math>
| |
| − |
| |
| − | : <math>E_j = \frac{I}{1- rand \frac{T_{up}-1}{T_{up}}}</math> : rand = random number between 0 and 1
| |
| − |
| |
| − | :<math>T_{up} = \left \{ {~ 1 keV \; threshold \;energy \;for \; \delta- ray \; production \atop T_{max} \; \;\;\; if \; T_{max} < 1 keV} \right .</math>
| |
| − |
| |
| − | : <math>I</math> = mean ionization energy
| |
| − |
| |
| − | :<math>E_2 \approx (10 eV) Z^2</math>
| |
| − |
| |
| − | :<math>\ln E_1 = \frac{\ln (I) - f_2 \ln (E_2)}{f_1}</math>
| |
| − |
| |
| − | :<math>f_1 + f_2 =1</math>
| |
| − |
| |
| − | :<math>f_2 =\left \{ {0 \; z=1 \atop \frac{2}{z} \; z \ge 2} \right .</math>
| |
| − |
| |
| − | The fluctuation model was comparted with data in
| |
| − |
| |
| − | K. Lassila-Perini and L. Urban, NIM, A362 (1995) pg 416
| |
| − |
| |
| − | The cross sections used for excitation and ionization may be found in
| |
| − |
| |
| − | H. Bichel, Rev. Mod. Phys., vol 60 (1988) pg 663
| |
| − |
| |
| − | === Range Straggling===
| |
| − |
| |
| − | ;Def of Range (R):
| |
| − | : The distance traveled before all the particles energy is lost.
| |
| − |
| |
| − | :<math>R \equiv \int_0^T \frac{dE}{\frac{dE}{dx}}</math>
| |
| − | : = theoretical calculation of the path length traveled by a particle of incident energy <math>T</math>
| |
| − |
| |
| − | : Note units: <math>\left [ R \right ] = \frac{g}{cm^2} ; \left [ \frac{dE}{dx} \right ] = \frac{MeV \cdot cm^2}{g}</math>
| |
| − |
| |
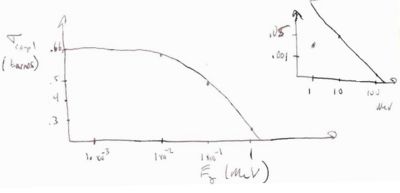
| − | the Energy Straggling introduced in the previous section can explain why identical particles penetrate material to different depths. The energy straggling results in Range straggling.
| |
| − |
| |
| − | If we do a shielding experiment where we have a source of incident particles of energy E and we count how many "punch" through a material of thickness (x) we would see a transmission coefficient <math>\left ( \frac{N_{out}}{N_{in}} \right) </math> which would look like
| |
| − |
| |
| − | [[Image:SPIM_RangeStraggling.jpg | 400 px]]
| |
| − |
| |
| − | ====Fractional Range Straggling ====
| |
| − |
| |
| − | <math>\frac{\sigma_R}{R} \equiv</math> fractional range straggling
| |
| − |
| |
| − | Assuming the energy loss of a non-relativistic heavy ion through matter follows a Gaussian (thick absorber)
| |
| − |
| |
| − | Then it can be shown that
| |
| − |
| |
| − | <math>\frac{\sigma_R}{R} \approx \frac{1}{2} \sqrt{\frac{M}{A}}</math>
| |
| − |
| |
| − | where
| |
| − |
| |
| − | : <math>M</math> = mass of the target electrons
| |
| − |
| |
| − | : <math>A</math> = atomic mass of the Projectile
| |
| − |
| |
| − | since
| |
| − |
| |
| − | :<math>m_e = 9.11 \times 10^{-31}</math> kg
| |
| − |
| |
| − | and
| |
| − |
| |
| − | : 1 a.m.u. = <math>1.66 \times 10^{-27}</math> kg
| |
| − |
| |
| − | then
| |
| − |
| |
| − | : <math>\frac{\sigma_R}{R} \approx \frac{1}{2} \sqrt{\frac{9.11 \times 10^{-31}}{1.66 \times 10^{-27}A}}</math>
| |
| − | : = 1.17 % if using a proton (A=1)
| |
| − |
| |
| − | The above is a "back of the envelope" estimate. The experimentally measured values for Cu, Al, and Be target using a proton projectile are
| |
| − |
| |
| − | [[Image:SPIM_RangeStrag_SigmaR_overR.jpg | 400 px]]
| |
| − |
| |
| − | If the incident projectile is an electron then <math>\frac{\sigma_R}{R} \approx \frac{1}{2}</math> making electron range straggling a vague concept.
| |
| − |
| |
| − | There are several definitions of electron range
| |
| − |
| |
| − | ;1.) Maximum Range (<math>R_0</math>):
| |
| − | :This range is defined using the continuous slowing down approximation (CSDA) in the electrons are assumed to have many collisions over very small dimensions making it appear to be continuous energy loss instead of discrete. The range is then calculated by integrating over these average energy losses <math>\frac{dE}{dx} \cdot s</math>.
| |
| − |
| |
| − | ;2.) Practical Range (<math>R_P</math>):
| |
| − | : This stopping distance is defined by extrapolating the electron transmission curve to zero (see below).
| |
| − |
| |
| − | [[Image:SPIM_PracticalRangStraggline_4Electrons.jpg | 400 px]]
| |
| − |
| |
| − | === Electron Capture and Loss ===
| |
| − | ====Bohr Criterion====
| |
| − | :"A rapidly moving nucleus is fully ionized if its velocity exceeds that of its most tightly bound electron"
| |
| − |
| |
| − | The Bohr Model:
| |
| − | :<math>\Rightarrow E = \frac{mz^2e^4}{8 \epsilon_0^2 h^2 n^2}</math>
| |
| − |
| |
| − | for the inner most electron (<math>n=1</math>)
| |
| − |
| |
| − | :Electron K.E. = <math>\frac{1}{2} mv^2 = \frac{mz^2e^4}{2(4\pi \epsilon_0)^2 \hbar^2} \Rightarrow v = \frac{z e^2}{4 \pi \epsilon_0 \hbar}</math>
| |
| − |
| |
| − |
| |
| − | :the fine structure constant <math>\alpha \equiv \frac{e^2}{4 \pi \epsilon_0 \hbar c} = \frac{1}{137}</math>
| |
| − |
| |
| − | :<math> v = zc \alpha</math>
| |
| − |
| |
| − | If <math>v > zc \alpha</math> the nucleus is fully ionized
| |
| − |
| |
| − | or
| |
| − |
| |
| − | if <math>\frac{z}{v/c} = \frac{z}{\beta} < \frac{1}{\alpha} = 137</math>
| |
| − |
| |
| − | alternatively if the ion is moving through a material with a speed such that
| |
| − |
| |
| − | :<math>\frac{z}{\beta} > \frac{1}{\alpha} =137</math>
| |
| − |
| |
| − |
| |
| − | Then electrons may be captured by the projectile and lost by the target.
| |
| − |
| |
| − | ==== Z-effective====
| |
| − | Describing the charge state of your heavy ion traveling through matter at a velocity below the Bohr criterion is very complicated. There is a competition between electron capture and loss. Accurate cross sections are needed to simulate the process reliably.
| |
| − |
| |
| − | Some insight into this process can be found using the Thomas-Fermi model
| |
| − |
| |
| − | : <math>V \propto \frac{Ze^{-r/a}}{r}</math>
| |
| − |
| |
| − | to describe an atom moving slow enough so it has captured many electrons but fast enough so its not neutral. In the Thomas-Fermi model the distribution of electrons in an atom is described as being uniformly distributed such that there are 2 electrons in each discrete volume of phase space( the space in which all possible states of a system are represented) defined using planks constant as <math>h^3</math>.
| |
| − |
| |
| − | For the purpose of simulations you would like a relationship for <math>Z_{eff}</math> in terms of <math>\beta</math> and <math>Z</math>.
| |
| − |
| |
| − | It is usually adequate to use fits for empirical data as long as we know that we are in the kinematic range in which those fits are valid.
| |
| − |
| |
| − |
| |
| − | when <math>E < 10</math> MeV the data indicates that
| |
| − |
| |
| − | : <math>Z_{eff} = Z(1 - e^{-\beta\frac{B}{Z^{2/3}}})</math>
| |
| − |
| |
| − | where
| |
| − |
| |
| − | : <math>B = 130 \pm 5</math>
| |
| − | :<math>Z_{eff} \equiv</math> effective charge f the projectile = <math>Z - \bar{q}_c</math>
| |
| − | : <math>Z</math> = number of protons
| |
| − | :<math>\bar{q}_c</math> = average number of captured electrons
| |
| − |
| |
| − |
| |
| − |
| |
| − | '''When calculating stopping power for E < 10 MeV you use <math>Z_{eff}</math> in the Bethe-Bloch equation.'''
| |
| − |
| |
| − | Note: As the ions charge state fluctuates while it slows down (or if accelerated through materials) you will need to recalculate the energy loss, and as a result you will get larger energy loss fluctuations in this energy range.
| |
| − |
| |
| − | For thin absorber you will look for stripping and loss cross sections.
| |
| − |
| |
| − | : Here a thin absorber is one whose thickness is less than the charge equilibrium distance defined as the distance traveled until the projectile's velocity is <math> v \ll zc\alpha</math>
| |
| − |
| |
| − | A rule of thumb is that a thin absorber for low energy ions has a thickness <math>\le \frac{5 \frac{\mu g}{cm^2}}{\rho}</math>
| |
| − |
| |
| − | For thick absorbers: The experimentally determined expression for the change in <math>Z_{eff}</math> from <math>Z</math> is
| |
| − |
| |
| − | :<math>\Delta Z_{eff} = \frac{1}{2} \sqrt{ \left [ Z_{eff} \left (1 - \frac{Z_{eff}}{Z} \right )^{1.67}\right ] }</math>
| |
| − |
| |
| − | === Multiple Scattering ===
| |
| − |
| |
| − | The Bethe-Bloch equation tells us how much energy is lost and GEANT4s calculation of this energy is described above.
| |
| − |
| |
| − | Now we need to know which direction the scattered particle goes after it has lost this energy.
| |
| − |
| |
| − | The work of Moliere describes the angular deflection of the particle which lost the energy thereby leading to a prediction of the Cross-section. GEANT4 though uses the more complete Lewis theory to describe Multiple Couloumb Scattering (MCS) sometimes generically referred to as multiple scattering.
| |
| − |
| |
| − | There are 3 regions in which coulomb scattering is calculated
| |
| − |
| |
| − | ; 1.) Single Scattering:
| |
| − | : For thin materials.
| |
| − | : If the probability of more than 1 coulomb scattering is small
| |
| − | :The use the Rutherford formula for <math>\frac{d \sigma}{d \Omega}</math>
| |
| − |
| |
| − | ;2.)Multiple Scattering:
| |
| − | : In this case the number of independent scatterings is large (N > 20) and the energy loss is small such that the problem can be treated statisticaly to obtain a probability distribution for the net deflection angle <math> [P(\theta)]</math> as a function of the material thickness that is traversed.
| |
| − |
| |
| − |
| |
| − | ;3.) Plural Scattering:
| |
| − | : If 1< N <math>\le</math> 20 then you can't use Rutherford to describe the scattering nor use a normal random statistical description.
| |
| − |
| |
| − | see E. Keil, Z. Naturforsch, vol 15 (1960), pg 1031
| |
| − |
| |
| − |
| |
| − | Reviews of rigorous multiple scattering calculations may be found in
| |
| − | : P.C. Hemmer, et. al., Phys. Rev, vol 168 (1968), pg 294
| |
| − |
| |
| − | ==== GEANT4's implementation of MSC (N>20) ====
| |
| − |
| |
| − | GEANT4 models MSC when N>20 using model functions to determine the angular and spatial distributions chosen to give the same moments of these distributions as the Lewis theory.
| |
| − |
| |
| − | :H.W. Lewis, Phys. Rev., vol 78 (1950), pg 526
| |
| − |
| |
| − | modern versions of the above are at
| |
| − |
| |
| − | : J.M. Fernandez-Varea, et. al., NIM, B73 (1993), pg 447
| |
| − | : I. Kawrakow, et. al., NIM, B142 (1998) pg 253
| |
| − |
| |
| − | When N>20 multiple scattering can be described as a statistical process using a modified version of the Boltzman transport equation from statistical mechanics.
| |
| − |
| |
| − | ;Note: The simulation step size is chosen such that (N>20), If you have materials so thin that N < 20 then GEANT4 will likely skip the material. (one way around this is to increase the thickness and change the density). If the material thickness can't be increased because its sandwhiched between two other materials then you will need to write a special step algorithm for the volume and have GEANT4 use it for the step.
| |
| − |
| |
| − |
| |
| − | Let <math>f(s,\vec{x},\hat{v}) \equiv</math> the distribution function for a system of incident particles traveling through a material.
| |
| − |
| |
| − | where
| |
| − |
| |
| − | :<math>s =</math> arc length of the particle's path through the material
| |
| − | :<math>\vec{x} =</math> position of a charged particle
| |
| − | : <math>\hat{v} =</math> direction of motion of the particle <math>\frac{\vec{v}}{|\vec{v}|}</math>
| |
| − |
| |
| − | The multiple scattering experienced by a single charged particle traveling through the material is then simulated by sampling from the distribution <math>f(s,\vec{x},\hat{v} )</math>
| |
| − |
| |
| − | The governing transport/diffusion equation is based on the continuity equation but with a "sink" term representing the possibility of collisions ejecting particles out of the volume.
| |
| − |
| |
| − | [[Image:SPIM_MultScatDiffEq.jpg | 400 px]]
| |
| − |
| |
| − | :<math>\frac{\partial f(s,\vec{x},\hat{v} ) }{\partial s} + \hat{v} \bullet \vec{\nabla}f(s,\vec{x},\hat{v} ) = N \int \sigma(\hat{v} \bullet\hat{v}^{\prime} )\left [ f(s,\vec{x},\hat{v}^{\prime} ) - f(s,\vec{x},\hat{v} ) \right ] d \hat{v}^{\prime}</math>
| |
| − |
| |
| − | where
| |
| − |
| |
| − | :<math>N</math> = number of atoms per volume
| |
| − | :<math>\sigma(\hat{v} \bullet\hat{v}^{\prime} )</math> = cross sections for elastic scattering per Solid angle <math>\left ( \frac{d \sigma}{d \Omega} \right )</math>
| |
| − |
| |
| − | To solve the above diffusion equation the distribution function, <math>f(s,\vec{x},\hat{v} )</math> is expanded in Spherical Harmonics ( <math>Y_{\ell}^m(\theta,\phi)</math> ) and <math>\sigma</math> expand in Legendre Polynomials (<math>P_N(cos \theta)</math>) since it has no <math>\phi</math> angle dependence.
| |
| − |
| |
| − | ;Note: For Coulomb Scattering in polar coordinates you can write the potential in terms of Legendre Polynomials such that:
| |
| − |
| |
| − | :<math>U=k \frac{q}{r}</math>
| |
| − | := <math>k\frac{q}{\sqrt{r^2-a^2-2ar \cos \theta}}</math> in polar coordinates
| |
| − | := <math>k\frac{q}{r} \sum_{n=0}^{\infty} P_n(\cos \theta) \left ( \frac{a}{r}\right )^n</math> (the sqrt term above is expanded using binomial series
| |
| − |
| |
| − | : <math>f(s,\vec{x},\hat{v} ) = \sum_{\ell,m} f_{\ell,m}(\vec{x},s) Y_{\ell}^m(\hat{v})</math>
| |
| − |
| |
| − | after substituting into the diffusion equation and doing the integral on the righ hand side you get
| |
| − |
| |
| − | :<math>\frac{\partial f_{\ell,m}(\vec{x},s) }{\partial s} + \frac{f_{\ell,m}(s,\vec{x},\hat{v} }{\lambda_{\ell}} = - \sum_{\lambda, i, j} \vec{\nabla} f_{i,j}(\vec{x},s ) \bullet \int Y_{\ell,m}^{\star} \hat{v} Y_{i,j} d \hat{v} \; \; \; \; \; \; \; \;\hat{v} = f(\theta.\phi)</math>
| |
| − |
| |
| − | where
| |
| − | : <math>\frac{1}{\lambda_{\ell}} = 2 \pi N \int_0^{\pi} \left [ 1-P_{\ell}(\cos \theta)\right ] \sigma(\theta) \sin(\theta) d \theta</math> = <math>\ell^{th}</math> transport mean free path for the <math>f_{\ell}</math> distribution function ( <math>\phi</math> symmetry is assumed making it <math>m</math> independent)
| |
| − |
| |
| − | From the above one can find the average distances traveled and the average deflection angle of the distribution. Again, see :
| |
| − |
| |
| − | : J.M. Fernandez-Varea, et. al., NIM, B73 (1993), pg 447
| |
| − |
| |
| − |
| |
| − | The "moments" of <math>f(s,\vec{x},\hat{v}) </math> are defined as
| |
| − |
| |
| − | :<math><z> = 2 \pi \int z f(s,\vec{x},\hat{v}) \sin(\theta) d \theta d |\vec{x}| = \lambda_1 \left [ 1-e^{-s/\lambda_1}\right ]</math> = mean geometrical path length
| |
| − | :<math><\cos(\theta)> = 2 \pi \int_{-1}^1 \sum_{\ell} P_{\ell}(\cos \theta) \int f(s,\vec{x},\hat{v}) \sin(\theta) d \theta d |\vec{x}| = e^{-s/\lambda_1}
| |
| − | </math>
| |
| − | :<math>\frac{1}{\lambda_1} = 2 \pi N \int_0^{\pi} \left [ 1-P_1(\cos \theta)\right ] \sigma(\theta) \sin(\theta) d \theta</math>
| |
| − |
| |
| − | Notice there are 3 lengths
| |
| − |
| |
| − | [[Image:SPIM_MultScatDiffEq_PathLength.jpg | 400 px]]
| |
| − |
| |
| − | :<math>s</math> = geometrical path length between endpoints of the step =<math> \left \{ {line \; if \; \vec{B} = 0 \atop arc \; if \; \vec{B} \ne 0 } \right .</math>
| |
| − | :<math>t</math> = true path length = actual length of the path taken by particle
| |
| − | :<math><z></math> - mean geometrical path length along the z-axis
| |
| − |
| |
| − | In GEANT4 the <math>\lambda_{\ell}</math>'s are taken from
| |
| − |
| |
| − | If 100 eV < K.E. of electron or positron < 10 MeV
| |
| − |
| |
| − | :D. Liljequist, J. Applied Phys, vol 62 (1987), 342
| |
| − | :J. Applied Phys, vol 68 (1990), 3061
| |
| − |
| |
| − | If K.E. > 10 MeV
| |
| − |
| |
| − | :R. Mogol, Atomic Data, Nucl, Data tables, vol 65 (1997) pg 55
| |
| − |
| |
| − |
| |
| − |
| |
| − | with <z> now known GEANT will try to determine "<math>t</math>" for the energy loss and scattering calculations.
| |
| − |
| |
| − | A model is used for this where
| |
| − |
| |
| − | :<math>t=\frac{1}{\alpha} \left [ 1 - (1- \alpha \omega z)^{\frac{1}{\omega}})\right ]</math>
| |
| − |
| |
| − | where
| |
| − |
| |
| − | : <math>\omega = 1 + \frac{1}{\alpha \lambda_{10}}</math>
| |
| − | : <math>\alpha =\left \{ {\frac{\lambda_{10} - \lambda_{11}}{s \lambda_{10}}\;\;\;\; K.E. \ge M_{particle} \atop \frac{1}{R}\;\;\;\; K.E. < M_{particle}} \right .</math>
| |
| − | : <math>s</math> = stepsize
| |
| − | : <math>\lambda_{10} - \frac{\lambda_1}{1-\alpha s}</math>
| |
| − | :<math>\lambda_{11} = \lambda_1</math> at end of strep
| |
| − |
| |
| − | while <math><cos \theta ></math> is calculable, GEANT4 evaluates <math>\cos (\theta)</math> from a probability distribution whose general form is
| |
| − |
| |
| − | :<math>g[\cos(\theta)] - p \left ( qg_1[\cos(\theta)] + (1=q)g_3[\cos(\theta)] \right ) + (1-p)g_2[\cos(\theta)]</math>
| |
| − |
| |
| − | where
| |
| − |
| |
| − | :<math>g_1(x) = C1e^{-a(1-x)}</math>
| |
| − | :<math>g_2(x) = \frac{C_2}{(b-x)^d}</math>
| |
| − | :<math>g_3(x) = C_3</math>
| |
| − |
| |
| − | :<math>C_1, C_2, C_3</math> are normalization constants
| |
| − | :<math>p,q,a,b,d</math> are parameters which follow the work reported in
| |
| − |
| |
| − | :V.L. Highland, NIM, vol 219 (1975) pg497
| |
| − |
| |
| − | The GEANT4 files in version 4.8 were located in
| |
| − |
| |
| − | /source/processes/electromagnetic/utils/src/G4VMultipleScattering.cc
| |
| − |
| |
| − | and
| |
| − |
| |
| − | /source/processes/electromagnetic/standard/src/G4MscModel.cc
| |
| − |
| |
| − | /source/processes/electromagnetic/standard/src/G4MultipleScattering.cc
| |
| | | | |
| | =Interactions of Electrons and Photons with Matter= | | =Interactions of Electrons and Photons with Matter= |
Class Admin
The ability to simulate nature using a computer has become a useful skill for physicists who work in disciplines ranging from basic research to video games. This class will teach you these fundamentals using a practical approach, based on a specific UNIX based programming environment, to simulate fundamental physics processes ranging from ionization and the photoelectric effect to producing anti-matter.
Homework
Homework is due at the beginning of class on the assigned day. If you have a documented excuse for your absence, then you will have 24 hours to hand in the homework after released by your doctor.
Class Policies
http://wiki.iac.isu.edu/index.php/Forest_Class_Policies
Instructional Objectives
- Course Catalog Description
- Simulations of Particle Interactions with Matter 3 credits. Lecture course with monte-carlo computation requirements. Topics include: Stopping power, interactions of electrons and photons with matter, hadronic interactions, and radiation detection devices.
Prequisites:Math 3360. Phys 3301 or 5561.
- Course Description
- A practical course applying theoretical descriptions of fundamental particle interactions such as the photoelectric effect, compton scattering and pair production to describe multiple interactions of particles with matter using the montecarlo method. A software package known as GEANT from CERN will be used that is freely available under the UNIX environment. The course assumes that the student has very limited experience with the UNIX environment and no experience with GEANT. Homework problems involve modifying and compiling example programs written in C++. A final project is required in which the student chooses a process to compare the predictions of GEANT with experimental data. A report is written in a format that would be publishable in a scientific journal. Publishing the report is not required but left as an option for the student.
Objectives and Outcomes
SPIM_ObjectiveNoutcomes
Homework Problems
HomeWork_Simulations_of_Particle_Interactions_with_Matter
Introduction
TF_SPIM_Intro
Energy Loss
TF_SPIM_StoppingPower
Ann. Phys. vol. 5, 325, (1930)
Interactions of Electrons and Photons with Matter
Bremsstrahlung
- Definition
- Radiation produced when a charged particle is deflected by the electric field of nuclei in a material.
- Note: There is also electron-electron brehmstrahlung but the interaction is with the electric field of the materials atomic electrons.
The Cross section formula is given in Formula 3Cs, pg 928 of reference H.W. Koch & J.W Motz, Rev. Mod. Phys., vol 31 (1959) pg 920 as
- Note
- Bethe & Heitler first calculated this radiation in 1934 which is why you will sometimes hear Bremsstrahlung radiation refererd to as Bethe-Heitler.
- [math]d \sigma = 4 Z^2r_e^2 \alpha \frac{d \nu}{\nu} \left \{ \left (1 + \left( \frac{E}{E_0} \right )^2 \right ) \left [ \frac{\phi_1(\gamma)}{4} - \frac{1}{3} \ln Z -f(Z)\right ] - \frac{2E}{3E_0} \left [ \frac{\phi_2(\gamma)}{4} - \frac{1}{3} \ln Z -f(Z)\right ] \right \} [/math]
where
- [math]E_0[/math] = initial total energy of the electron
- [math]E[/math] = final total energy of the electron
- [math]\nu = \frac{E_0-E}{h}[/math] = energy of the emitted photon
- [math]Z[/math] = Atomic number = number of protons in target material
- [math]\gamma = \frac{100 m_ec^2 h \nu}{E_0 E Z^{1/3}}[/math] = charge screening parameter
Coulomb correction to using the Born approximation (approximation assumes the incident particle is a plane wave interacting with a static E-field the correction accounts for changes iin the plane wave due to the presence of the field) Charge screening and the coulomb correction are different effects that have been shown to be additive/independent. File:Haug 2008.pdf
- [math]f(Z) = (Z \alpha)^2 \sum_1^{\infty} \frac{1}{ n [ n^2 + (Z \alpha)^2]}[/math]
- [math]\sim (Z \alpha)^2 \left \{ \frac{1}{1+(Z \alpha)^2} +0.20206 - 0.0369(Z \alpha)^2 + 0.0083 (Z \alpha)^4 - 0.002 (Z \alpha)^6\right \}[/math]
- [math]\alpha = \frac{1}{137}[/math]
- [math]\phi_1[/math] and [math]\phi_2[/math] = screening functions that depend on Z
if [math]Z \ge 5[/math]
- [math]\phi_1(\gamma) = 20.863 - 2 \ln[1+(0.55 \gamma)^2] - 4[1-0.6e^{-0.98} - 0.4e^{-3 \gamma/2}][/math]
- [math]\phi_2(\gamma) = \phi_1(\gamma) - \frac{2}{3}(1+6.5 \gamma + 6 \gamma^2)[/math]
For Z<5 see Tsai, Rev.Mod. Phys., vol 46 (1974) pg 815
- if [math]3 \ge Z \lt 5[/math] use Equation 3.46 and 3.47
- if [math] Z \lt 2[/math] use Equation 3.25 and 3.26
- Note
- Energy loss via Bethe-Bloch is due to coulomb deflection and is a continuous process while Bremsstrahlung is a discrete process (emission of photons)
- We now know 2 ways charged particles can loose energy when passsing through matter.
- Energy loss
- [math]\left ( \frac{dE}{dx} \right )_{tot} = \left ( \frac{dE}{dx} \right )_{rad} + \left ( \frac{dE}{dx} \right )_{col}[/math]
- [math]{rad} \Rightarrow[/math] : Bremsstrahlung
- [math]{col} \Rightarrow[/math] : Bethe-Bloch (collision)
- [math]-\left ( \frac{dE}{dx} \right )_{rad} = N \int_o^{\nu_0} \left ( h \nu \right ) \left ( \frac{d \sigma}{d \nu} \right ) d \nu[/math]
where
- [math]N = \frac{ number\; atoms}{cm^3} = \frac{\rho N_a}{A} = \frac{density \;\times\; Avagadros\;\;Number}{Atomic number}[/math]
- [math]\left ( h \nu \right )[/math] = Energy of emmitted photon
- [math]\left ( \frac{d \sigma}{d \nu} \right )[/math] = Probabitlity of Energy loss
The quantity[math] \Phi_{rad} [/math] is defined such that
- [math]\Phi_{rad} \equiv \frac{1}{E_0} \int_o^{\nu_0} \left ( h \nu \right ) \left ( \frac{d \sigma (E_0,\nu)}{d \nu} \right ) d \nu[/math]
[math]\Phi_{rad}[/math] is a macroscopic function of a given material rather than just the energy [math]\nu[/math] which we will use to define a common property of materials known as the radiation length [math]\left ( R_0=\frac{1}{N\Phi_{rad}} \right )[/math]
- [math]\Phi_{rad} = 4Z^2r_e^2 \alpha \left \{ { \left [ \ln(\frac{2E}{m_ec^2}) - \frac{1}{3} - f(z) \right ] \gamma \gt \gt 1 \atop \left [ \ln(183E^{-1/3}) + \frac{1}{18} - f(z) \right ] \gamma \sim 0} \right .[/math]
where
- [math]\gamma \gt \gt 1[/math] case is no screening and [math]1 \ll \frac{E_0}{m_e c^2} \lt \frac{1}{\alpha Z^{1/3}}[/math]
- [math]\gamma \; \sim \; 0[/math] case has [math] \frac{E_0}{m_e c^2} \gg \frac{1}{\alpha Z^{1/3}}[/math]
The energy loss equation becomes
- [math]- \frac{dE}{dx} = N E_0 \Phi_{rad}[/math]
- Note
- for intermediate value of [math]\gamma[/math] you need to integrate numerically
- [math]\left ( \frac{dE}{dx} \right )_{rad}\propto Z^2E[/math] : Bremsstrahlung
- [math]\left ( \frac{dE}{dx} \right )_{col}\propto Z \ln (E)[/math] : Bethe-Bloch
The illustration below shows the relative contributions of Bethe-Bloch and Bremsstrahlung to the total energy loss according to the above functional dependence. At low energies the physics of collisions dominates the loss (Bethe-Bloch) and as energy increases the discrete loss by radiation begins to dominate.
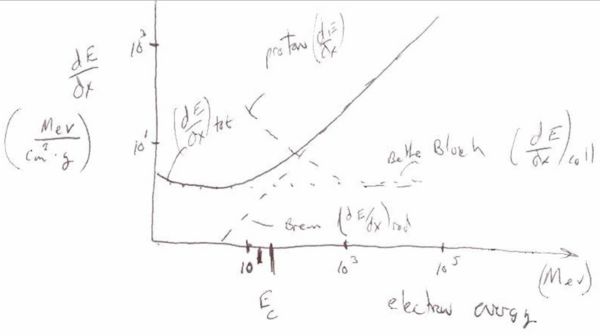
- Critical Energy[math] E_C[/math]
At the critical energy [math]E_C[/math] the two energy loss processes contribute equally to the total energy lost by a charged particle interacting with matter.
- [math]E_C \equiv[/math] energy at which [math]\left ( \frac{dE}{dx} \right )_{rad} = \left ( \frac{dE}{dx} \right )_{col}[/math]
In the PDG
- [math]E_C \sim \frac{800 MeV}{Z+1.2}[/math]
- Examples
Critical Energy E_C
|
| Material
|
[math]E_C[/math] (MeV)
|
| Pb
|
9.51
|
| Fe
|
27.4
|
| Cu
|
24.8
|
| Al
|
51
|
Electron-Electron Bremsstrahlung
- Electron electron bremsstrahlung
- The radiation produced as 2 electrons pass near eachother
- [math]d \sigma[/math] is essentially the same except you have [math]z=1[/math] thereby adding a [math]Z[/math] term and not a [math]Z^2[/math] term
reference:pg 947 from Koch and Motz, Rev. Mod. Phys, vol 31 (1959) pg 920 File:SPIM Koch andMotz RevModPhysv31 1959pg920.pdf
as a result
[math]d \sigma_{tot} = \frac{Z(Z+1)}{Z^2} d \sigma_{Brem}[/math]
- = [math]4 Z(Z+1)r_e^2 \alpha \frac{d \nu}{\nu} \left \{ \left (1 + \left( \frac{E}{E_0} \right )^2 \right ) \left [ \frac{\phi_1(\gamma)}{4} - \frac{1}{3} \ln Z -f(Z)\right ] - \frac{2E}{3E_0} \left [ \frac{\phi_2(\gamma)}{4} - \frac{1}{3} \ln Z -f(Z)\right ] \right \} [/math]
Most calculations ignore electron-electron Brehmsstrahung because its linear in Z and doesn;t become important until low Z where measured atomic form factors are actually used and not Form factors calulated by the Thomas-Fermi-Moliere Model (Z>4).
Coherent Bremsstrahlung
The above equations represent the physics of incoherent bremsstrahlung production.
http://137.99.79.133/halld/tagger/references/inelasticBrems-94.pdf
Radiation Length (Xo)
- Radiation Length[math] (X_0)[/math]
- The distance an electron travels through matter until loosing [math]\frac{1}{e}[/math] of its energy due to radiation [math]\left ( \frac{dE}{dx} \right )_{rad}[/math].
in the high energy limit where [math]\left ( \frac{dE}{dx} \right )_{col}[/math] can be ignored [math]( E \gt E_C )[/math]
- [math]\frac{dE}{dx} = NE_0 \Phi_{rad} \Rightarrow \int_{E_0}^{E} \frac{dE}{E} = -\int_0^X N \Phi_{rad} dx[/math]
- [math]\Rightarrow \ln(\frac{E}{E_0}) =-N \Phi_{rad}X[/math]
or
- [math]E = E_0 e^{-N \Phi_{rad}X} = E_0 e^{-\frac{X}{X_0}}[/math]
where
- [math]X_0 \equiv \frac{1}{N \Phi_{rad}}[/math] = Radiation Length of a given material
ie:
- if [math] X = X_0[/math] Then [math]E=\frac{1}{e} E_0[/math] = Energy of electron after traveling a distance of [math]X_0[/math] through the material
Table of Radiation Lengths for several materials
|
| Material
|
[math]X_0[/math] (cm)
|
| Air
|
30,050
|
| Al
|
8.9
|
| Cu
|
1.43
|
| Fe
|
1.76
|
| H2O
|
36.1
|
| NaI
|
2.59
|
| Pb
|
0.56
|
| Polystyrene
|
42.9
|
| Scintillators
|
42.2
|
- If we have complete screening [math] (\gamma=0)[/math]
- Then [math]\frac{1}{X_0} = N \Phi_{rad} = 4 \alpha r_e^2 \frac{N_A}{A} \left \{ Z^2 \left [ L_{rad} - f(Z)\right ] + ZL_{rad}^{\prime}\right \}[/math]
- = [math]\frac{Z^2 \left [ L_{rad} - f(Z)\right ] + ZL_{rad}^{\prime}}{716.408 \frac{g}{cm^2}A}[/math]
where
- [math]L_{rad} \equiv \frac{1}{4} [\phi_1(\gamma=0) - \frac{4}{3} \ln(Z)] = \left \{ {1 + \int_0^{m_e} [ 1-\frac{F(q)}{Z}]^2 \frac{dq}{q} \;\;\; Z\le4\atop \ln(184.15 Z^{-1/3} \;\;\; Z\gt 4} \right . [/math]= radiation logarithm for elastic Atomic scattering
- [math]L_{rad}^{\prime} \equiv \frac{1}{4} [ \phi_2(\gamma=0) - \frac{8}{3}\ln Z]= \left \{ {1 + \frac{1}{2}\int_0^{m_e} \frac{G_2^{inel}(t)}{Z}\frac{dt}{t} \;\;\; Z\le4\atop \ln(1194 Z^{-2/3} \;\;\; Z\gt 4} \right .[/math] = radiation logarithm for inelastic Atomic scattering
- [math]f(Z) = \alpha^2 Z^2 \left [ \frac{1}{1+\alpha^2 Z^2} + 0.20206 - 0.0369 \alpha^2 Z^2 + 0.0083 \alpha^4 Z^4 -0.002 \alpha^6 Z^6 \right ][/math] :Z < 92
- Quick [math]X_0[/math] Estimates
- [math] X_0 = \frac{716.4 \left ( \frac{g}{cm^2} \right ) A }{Z(Z+1) \ln \left ( \frac{287}{\sqrt{Z}} \right )}[/math]
- Examples of Radiation length
- [math]\frac{1}{e} = \frac{1}{2.72} \sim \frac{1}{3}[/math]
- an electron has lost 1/3 of its original energy after traveling 1 radiation length (1 [math]X_0[/math]) through the material
- [math]\frac{1}{e^2} \sim \frac{1}{7}[/math]
- an electron has lost 1/7 of its original energy after traveling 2 radiation lengths (2 [math]X_0[/math]) through the material
- [math]\frac{1}{e^3} \sim \frac{1}{20}[/math]
- an electron has lost 1/20 of its original energy after traveling 3 radiation lengths (3 [math]X_0[/math]) through the material
- After 2.3 radiation lengths the electron energy is down by a factor of 10 from its original value.
Bremsstrahlung in GEANT 4
GEANT4 uses an energy cut off [math](T_c, k_c)[/math] to decide whether to use a continuous energy loss algorithm (msc, Bethe-Bloch, soft photons) or to generate a secondary particle (photon) and use Bremsstrahliung.
- [math]T_C[/math] = incident particle K.E. cutof = secondary particle production threshold
- [math]k_c[/math] = photon energy cutoff below which photons are treated as continuous energy loss.
- if [math]E_{secondary}\lt T_C[/math] then no photon is created and the effect of the soft photon reaction is treated as a continuous energy loss via
- [math]E_{loss}^{Brem} (Z,T,k) = \int_0^{k_c} \left ( \frac{ d \sigma(z,T,k)}{dk}\right ) k dk[/math] = continuous energy loss via "soft" photon emission
- [math]\frac{ d \sigma(Z,T,k)}{dk}[/math] = cross sections parametrerized by the Evaluated Electrons Data Library (EEDL)
- reference: J. Tuli, "Evaluated Nuclear Structure Data File", BNL-NCS - 51655 -Rev 87, 1987 from Brookhaven Nat. Lab
- see National Nuclear Data Center:
- Note
- Soft photons are photons created in the scattering process which have less energy than the energy of the particles participating in the interaction. Soft photon are not energtic enough to be detected.
To improve simulation speed though, GEANT 4 actually uses a fit to the above cross sections such that
- [math]E_{loss}^{Brem} (Z,T,k) = (2 - C_{th}Z^{1/4}) \frac{Z(Z+\epsilon_{\ell})(T+m)^2}{T+2m} \left [ \frac{k_C}{T}\right ]^{\beta} \frac{a+b\frac{T}{T_{\ell m}}}{1+c \frac{T}{T_{\ell m}}} \frac{f_{\ell}}{N_a}[/math]
where
- [math]m[/math] = electron mass
- [math]T[/math] = kinetic energy of incident particle
- [math]N_a[/math] = Avagadros number
- [math]\epsilon , \beta, C_{th}, a, b, c[/math] = constants
- [math]f_{\ell}[/math] = polynomial (in log(T) ) chosen to fit the data
- if [math]E_{secondary}\gt T_C[/math] then a photon is created and tracked
- The energy of the emitted photon is determine by sampling a probability distribution from
- S. Seltzer and M. Berger, Atomic Data & Nucle. Data tables, vol 35 (1986) pg 345-418
and
- the angular distribution ([math]\cos(\theta)[/math]) is sampled according to
- E. Acosta, Appl. Phys. Letter, vol 80 # 17 (2002) pg 3228-3230
Note
- The MC program PENELOPE was used to generate the energy distributions that are sampled
- GEANT4 uses a modified version of base equations for [math]e^+e^-[/math] bremsstrahlung with model corrections for [math]e^+[/math]
- LPM effect
- There is also a correction kown as the Landau Pomeranchuk Migdal (LPM) effect which corrects for multiple scattering experiences by the electron during the scattering which causes the emission of a photon.
Bragg's Rule for compound materials
The radiation length for compounds and mixtures is determined by parallel weighting (resistors in parallel)
- [math]\frac{1}{L_{rad}} = \omega_1 \left ( \frac{1}{L_{rad}} \right )_1 + \omega_2 \left ( \frac{1}{L_{rad}} \right )_2[/math]
where
- [math]\omega_1[/math] = fraction , by wieght, of each element in the mixture/compound.
- [math]= \frac{a_i A_i}{A_m}[/math]
- [math]a_1[/math] = # of atoms of element "i"
- [math]A_i[/math] = atomic # of element "i"
- [math]A_m = \sum a_i A_i[/math] = effective atomic mass of the compound/mixture
Photo-electric effect
The photo-electric effect identifies the physics process by which bound electrons in an atom are liberated by an interaction with an incident photon.
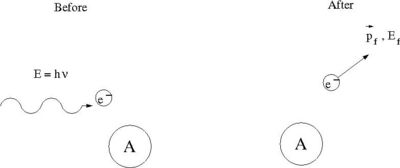
- [math]E_f = E-E_B = h \nu - E_B[/math]
where
- [math]h\nu[/math] = incident photon energy
- [math]E_B[/math] = electron binding energy
Moseley's Law
Moseley's law approximates the binding energies of electrons in atoms as
- [math]E_B = 13.605 \frac{\left ( Z-k_s \right )^2 }{n^2}[/math] (eV)
X-ray electron shells are labeled K,L,M
| Shell |
n |
Spect. Notation (low E) |
Spect. Notation (High E) |
k_s
|
| K |
1 |
[math]1S_0[/math] |
|
3
|
| L |
2 |
[math]2P_{3/2} , 2P_{1/2}[/math] |
3P{3/2} |
5
|
- Example
- Binding Energies for Argon (A=18) "Chemical Rubber Company Handbook of Chemistry and Physics", CRC press. Boca Raton FL, 81st ed, 2000.
| Shell |
n |
Spect. Notation |
Binding Energy (eV)
|
|
|
|
Measured |
GEANT4 |
Moseley
|
| [math]K[/math] |
1 |
[math]1S[/math] |
3218 |
3178 |
3061
|
| [math]L_{I}[/math] |
2 |
[math]2S[/math] |
328 |
313.5 |
575
|
| [math]L_{II}[/math] |
2 |
[math]2P_{1/2}[/math] |
251 |
247 |
575
|
| [math]L_{III}[/math] |
2 |
[math]2P_{3/2}[/math] |
248.4 |
247 |
575
|
Binding energies for a few common elements
| Element |
Binding Energy (eV)
|
|
n=1 |
n=2 |
n=3
|
| B |
201 |
14.2 |
8.3 |
|
|
| C |
298 |
17.9 |
11.4 |
|
|
| N |
450 |
26 |
15 |
|
|
| O |
548 |
33 |
13.6 |
|
|
| Na |
1083 |
71 |
38 |
5.2 |
|
| Mg |
1313 |
94 |
55 |
7.7 |
|
| Al |
1573 |
126 |
81 |
11 |
6
|
| Si |
1854 |
157 |
107 |
15 |
8.2
|
| P |
2167 |
195 |
141 |
20 |
10.5
|
| S |
2490 |
236 |
172 |
21.3 |
10.4
|
| Cl |
2844 |
279 |
210 |
25 |
13
|
| K |
3615 |
386 |
303 |
41 |
25
|
Photo-electric cross section
- the most general expression
- [math]\frac{d \sigma}{d \Omega} = 32 \frac{e^2}{4 \pi \hbar c} | \vec{k}^{\prime} | \frac{\hbar}{mc} \frac{c}{\omega} \left ( \frac{z}{a_o} \right )^5 \frac{ \left ( \hat{\epsilon} \cdot \vec{k}^{\prime} \right ) ^2}{ \left [ \frac{z^2}{a_0^2} + q^2 \right ]^4 } [/math]
where
- [math]\vec{k}^{\prime} = \frac{\vec{p}}{h}[/math] = scattered electron wave number [[math]\frac{1}{m}[/math] ]
- [math]\omega = c | \vec{k} |[/math] = incident photon wave frequency
- [math]a_o = \frac{\hbar^2}{(mc)^2}[/math]
- [math]\hat{\epsilon}[/math] = incident photon polarization
- [math]\vec{q} = \vec{k} - \vec{k}^{\prime}[/math] = momentum given to the atom divided by Plank's constant (h)
if the electron's K.E. after emission is larger than its binding energy
then
- [math]k^{\prime} \approx \left ( \frac{2m \omega}{\hbar} \right )^{1/2}[/math]
- [math]a_0 = \frac{r_0}{\alpha^2}[/math]
- [math]\hat{\epsilon} \cdot {\vec{k}}^{\prime} = k^{\prime} \sin(\theta) \cos(\phi)[/math]
[math]\Rightarrow[/math]
- [math]\frac{d \sigma}{d \Omega} = \alpha^4 r_0^2 Z^5 \left ( \frac{mc^2}{\hbar \omega}\right)^{7/2} \frac{4 \sqrt{2} \sin^2(\theta) \cos^2(\phi)}{\left [ 1 - \frac{v}{c}\cos(\theta)\right ]^4} [/math]
For K shell emmission
- [math]\sigma = 4 \sqrt{2} \frac{8 \pi r_o^2}{3} \alpha^4 Z^5 \left( \frac{mc^2}{\hbar \omega}\right)^{7/2}[/math]
at higher energies [math](\hbar \omega \gg mc^2 )[/math] (the ultra-relativistic limit
- [math]\sigma = \frac{3}{2} \frac{8 \pi r_o^2}{3} \alpha^4 Z^5 \left( \frac{mc^2}{\hbar \omega}\right)[/math]
References
http://physics.nist.gov/PhysRefData/Xcom/html/xcom1.html
http://www-amdis.iaea.org/LANL/
http://www.nist.gov/pml/data/ionization/index.cfm
Mass Attenuation Coefficient
The mass attenuation coefficient [math](\frac{\mu}{\rho})[/math] is used to describe the attenutation of a photon interacting with matter via the photo-electric effect ( absorption), coherent scattering (Rayleigh), incoherent scattering (Compton), or pair production.
- [math]\mu[/math] = linear photo-electric attenutaion
- [math]\rho[/math] = density of the material
- [math]\frac{\mu}{\rho} = \frac{\sigma_{PE}}{amu}[/math]
- Eample
- Below is an example of the mass atenuation coefficeint as a function of the incident photon energy
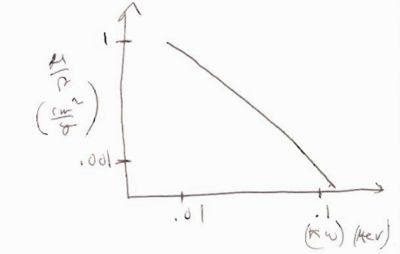
a 10 keV photon (0.01 MeV) will have [math]\frac{\mu}{\rho} = 1 \frac{cm^2}{g}[/math] when traveling through water [math](\rho = 1 \frac{g}{cm^3})[/math]
- [math]\Rightarrow \mu = 1 \frac{cm^2}{g} \rho = 1 \frac{1}{cm}[/math] = attenuation coefficient
- [math] I = I_0 e^{-\mu x}[/math] = intensity of light
- if [math]I= \frac{I_0}{2}[/math]
- [math]\Rightarrow x = \lambda_{1/2}[/math] = half length = [math]- \frac{1}{\mu} \ln (\frac{1}{2})[/math] = 0.69 cm
This means that 1/2 of the photons impinging on water get absorbed by the water atoms after a depth of 0.69 cm.
- Scaling
- Sometimes when [math]\frac{\mu}{\rho}[/math] is not available for your material you can scale a [math]\frac{\mu}{\rho}[/math] of a material with similar atomic number using the equation
- [math]\left ( \frac{\mu}{\rho} \right)_{unknown} = \left ( \frac{\mu}{\rho} \right)_{known} \left [ \frac{Z^n}{A \rho}\right][/math]
where the coefficient[math] n[/math] varies with the photon energy from 4 [math]\rightarrow[/math] 5 according to:

GEANT4
GEANT4 uses a parameterization of photon absorption cross sections to determine the mean free path, atomic shell data to determine the ejected electron energy, and the k-shell angular distribution to determine the direction of the ejected electron.
The fit to the photoabsorption cross sections
- The photoabsorption cross section is parametrized according to
- [math]\sigma(Z,E_{\gamma}) = \frac{a(Z,E_{\gamma})}{E_{\gamma}} + \frac{b(Z,E_{\gamma})}{E^2_{\gamma}} + \frac{c(Z,E_{\gamma})}{E^3_{\gamma}} + \frac{d(Z,E_{\gamma})}{E^4_{\gamma}}[/math]
where
- [math]a(Z,E_{\gamma}) ,\; b(Z,E_{\gamma}) ,\; c(Z,E_{\gamma}), \;d(Z,E_{\gamma})[/math] are determined by a least squares fit to the data as outlined in
F. Biggs & R. Lighthill, Sandia Lab Preprint, SAND 87-0070 (1990)
File:Biggs Lighthill SandiaPreprint 87-0070.pdf
You select [math]E_{\gamma}[/math] by sampling from a distribution generated by the above cross section.
The mean free path ([math]\lambda[/math]) of the photon through the material is given by
- [math]\lambda(E_{\gamma}) = \frac{1}{\sum_i N_i \sigma(Z_i,E_{\gamma})}[/math]
where
- [math]N_i = \frac{\mbox{number of Atoms of} \quad i^{th} \quad\mbox{element } \quad Z_i \quad \mbox{in the material}}{\mbox{Volume}}[/math]
K.E. of ejected electron
Given that a photo-electric event happens then the energy of the ejected electron is given by
- [math]T_{p.e.} = E_{\gamma}-B_{shell}(Z_i)[/math]
where
- [math]E_{\gamma}[/math] = energy of the incident photon
- [math]B_{shell}(Z_i)[/math] = electron shell energy from the closest available atomic shell as tabulated in data/G4EMLOW/fluor/binding.dat
The shell is selected according to the shell cross sections
Electron direction
The ejected electron is chosen by an angle according to the Souter-Gavrila distribution (Gavrila_M._Phys.Rev._vol113_1959_pg514) in the "standard" package such that
- [math]\cos(\theta) = \frac{rnd + \beta}{rnd\times \beta +1}[/math]
where rnd is a random number chosen such that
- [math]\frac{1-\cos^2(\theta)}{(1-\beta \cos(\theta))^2} \times \left [ 1 + b(1-\cos(\theta) \right ] \lt rnd \times \left \{ { \gamma^2(1+b(1-\beta)) \quad \gamma \lt 2 \atop \gamma^2(1+b(1+\beta) ) \quad \mbox{otherwise} } \right .[/math]
- [math]b = \frac{\gamma (\gamma -1) ( \gamma -2)}{2}[/math]
- [math]\gamma = 1+ \frac{\mbox{K.E.}_{e^-}}{m_ec^2}[/math]
Physics Models
G4PhotoElectricEffect
This model will generate an ionized electron which is about the same as the incident photon energy. Don't use this one if your simulation is sensitive to atomic energy levels (ie; looking at keV energy effects). This should be O.K. if you are just interested in attenuating photons.
G4LowEnergyPhotoElectric
This process will generate ionized electrons for each possible electron binding energy which is less than the incident photon energy. It should be cross section weighted.
This model seems to break when [math]E_{\gamma} \le[/math] 100 keV (GEANT4 version 4.8)
PAI Model
PhotoAbsorption Ionizaton (PAI) Model
The PAI model uses a least squares fit of a 4th order polynomial in [math]\frac{1}{\omega}[/math] to the experimental photoabsorption data for the cross section such than
- [math]\sigma(\omega) = \sum_i^4 \frac{a_k(E)}{\omega^k}[/math]
where
- [math]a_k(E)[/math] = fit coefficent for energy bin [math]E[/math]
- [math]\omega[/math] = energy transfered in the ionization collision
Compton Scattering
Compton scattering is like the photo-electric effect except the photon isn't absorbed but scattered by atomic electrons.
"Ideal" compton scattering is described in terms of free electrons.

The collision is elastic
- [math]\lambda^{\prime} = \lambda + \lambda_C (1-\cos(\theta)) = \frac{2 \pi}{\omega^{\prime}} = \frac{ch}{E_{\gamma}^{\prime}} = \frac{12,400 \mbox{Angstroms}}{E_{\gamma}^{\prime}}[/math]
- [math]\lambda_C[/math] = electron compton wavelength = [math]\frac{h}{m_ec} = 2.43 \times 10^{-12} m[/math]
- [math]E_k = \hbar \omega \frac{\lambda_C}{\lambda} \frac{1- \cos(\theta)}{1 + \frac{\lambda_C}{\lambda} \left (1 - \cos(\theta) \right )}[/math] = electron final kinetic energy
- [math]\phi = \cot \left [ \left ( 1+ \frac{\lambda_C}{\lambda}\right ) tan(\frac{\theta}{2}\right ][/math] = ejected electron angle w.r.t original photon direction
- Note
- [math]\phi_{max} = \frac{\pi}{2}[/math] : No electrons can be backscattered in the compton process.
- The photon can backscattered
- [math]\theta = \pi[/math] = Max energy transfered to the [math]e^-[/math]
- [math]E_k(max) = \frac{2 \hbar \omega \lambda_C}{\lambda + 2 \lambda_C}[/math] = The max energy transfer point corresponds to the "compton" edge
- Example
- Find [math] E_k(max)[/math] of the compton edge for a given [math]E_{\gamma}[/math].
- [math]E_k(max) = \frac{\hbar \omega }{\frac{\lambda}{2 \lambda_C} + 1} = \frac{E_{\gamma} }{\frac{\lambda}{2 \lambda_C} + 1}[/math]
- [math]\lambda = \frac{c}{\nu} = \frac{c h}{E_{\gamma}}[/math]
- [math]E_k(max) =\frac{E_{\gamma} }{\frac{c h}{2 \lambda_C E_{\gamma}} + 1} =\frac{E_{\gamma} }{\frac{3 \times 10^8 \frac{m}{s} 4.14 \times 10^{-15} \frac{eV}{s}}{2 \times 2.43 \times 10^{-12} m E_{\gamma}} + 1}[/math]
- [math]\approx 4 \times 10^{-6} \frac{E_{\gamma}^2}{1 + 4 \times 10^{-6} E_{\gamma}}[/math]
- If [math]E_{\gamma}[/math] = 8 keV
- Then [math]E_k(max) \approx 256[/math] eV = max energy lost by photon and given to electron
Cross Section
The Klein-Nishina formula (Oskar Klein & Yoshio Nashina, Z. fur Phys., vol 52 (1929), pg 853 ) is given as
- [math]\frac{d \sigma}{d \Omega} = \frac{r_e^2}{2} \frac{1 + \cos^2(\theta) + \frac{\xi^2 \left [ 1+ \cos(\theta) \right ]^2}{1 + \xi \left( 1+ \cos(\theta) \right)}}{\left[ 1+ \xi (1-\cos(\theta) ) \right ]^2}[/math]
where
- [math]\xi = \frac{h \nu}{m_e c^2} = \frac{E_{\gamma}}{E_0^{e^-}} = \frac{E_{\gamma}}{0.511 MeV} \approx 2\frac{E_{\gamma}}{MeV}[/math]
- Note
- The above cross section is for a free electron. Multiple by [math]Z[/math] (the number of electrons in the target) to get the atomic cross section.
After integrating over [math]d \Omega[/math]
- [math]\sigma_{compt} = 2 \pi r_e^2 \left \{ \frac{1+\xi}{\xi^2} \left [ \frac{2(1+\xi)}{1 + 2\xi} - \frac{1}{\xi} \ln(1+2 \xi) \right ]\right \}[/math]
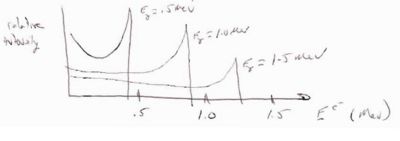
Energy Distribution
The compton electron energy distribution can be evaluated from the differential cross section below
- [math]\frac{d \sigma}{d E^{e^-}} = \frac{\pi r_e^2}{m_e c^2 \xi^2} \left [ 2 + \frac{s^2}{\xi^2 (1-s)^2} + \frac{s}{1-s} \left ( s - \frac{2}{\xi}\right )\right ][/math]
where
- [math]s = \frac{E^{e^-}}{h \nu} = \frac{E^{e^-}}{E_{\gamma}}[/math]
- [math]\xi \approx 2 E_{\gamma}[/math]
- [math]r_e^2 = 0.794[/math] barns
- [math]m_e c^2 = 0.511[/math] MeV
GEANT 4
GEANT 4 parametrized the Compton cross section to reproduce the data down to 10 keV using the expression
- [math]\sigma(Z,E_{\gamma}) = \left [ P_1(Z) \frac{\log(1+2 \xi)}{\xi} + \frac{P_2(Z) + P_3(Z) \xi + P_4(Z) \xi^2}{1 + a \xi + b \xi^2 + c \xi^3} \right ][/math]
- [math]P_i(Z) = d_i Z + e_i Z^2 + f_i Z^3[/math]
- [math]1 \le Z \le 100[/math]
- [math] a,b,c, d_i, e_i, f_i[/math] are determined from fit
The data used in the fit may be found in
- Hubbell, Grimm, & Overbo, J. Phys. Chem. Ref. Data 9, (1980) pg 1023
- H. Storm, Nucl. Data Tables, A7 (1970) pg 565
In addition to the default and low energy models which come with GEANT4 (as was available with the Photo Electric effect), there is also a model called "G4LECS" which may be installed.
- Models
- a.) G4ComptonScattering: listed as "compt" in the process name. No Rayleigh scattering in the model.
- b.) G4LowEnergyCompton: Process name is "LowEnCompton" in the tracking code. It has errors in the treatment of Rayleigh scattering and does not account for doppler broadening (the effect of bound electron momentum on the scattered particle energies).
- c.) G4LECS: Bound electron effects are corrected for on an :shell-by-shell" basis. Rayleigh scattering is modeled using the coherent scattering cross section and form factor data. The Doppler broadening effect is included ( a result of the compton telescope simulation work).
- Note
- Thomson & Rayleigh scattering are classical processes related to Compton scattering. Klein-Nishina formula reduces to the Thomson cross section at low energies such that [math]\sigma_{Thompson} = \frac{8 \pi}{3} r_e^2[/math]. Thomson scattering produces polarized light because at these low non-relativistic energies the particle that absorbs the photon emits it in a direction perpendicular to its motion, that motion is the results of sees the oscillating E & M wave from the incident photon. Rayleigh scattering (why our sky is blue) is photon scattering from an atom as a whole, coherent scattering. No energy is transfered to the Medium in either case, [math]\gamma[/math] only changes direction. Rayleigh scattering is the elastic scattering of the photon from a particle that is smaller than the wavelength of the light. Mei theory is used to describe elastic scattering from particles that are larger than the wavelength of the incident photon.
Pair Production
Pair production is similar to the Bremsstrahlung process.
Remember, in Bremsstrahlung the incident charged particle interacts with the [math]\vec{E}[/math] of the Nucleus (or shell electron)
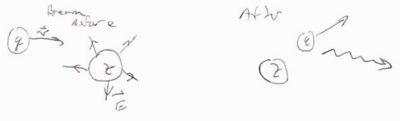
In pair production a photon interacts with the [math]\vec{E}[/math] of the Nucleus.

when the recoil of the atom is taken into account
- [math]E_{threshold} = 2 m_e(1+\frac{m_e}{M_A})[/math] = Threshold energy for pair production from an atom of mass [math]M_A[/math]
- Note
- You can also have photon-electron pair production analogous to electron-electron bremsstrahlung production.
Pair Production Cross Section
The pair production cross section is given by Equation 6.35 in (Bethe, Phys. Rev., vol. 93 (1964) pg 768)
at small angles
A version which assumes small angles is given in Eq 7.35 of the same reference as the triple differential cross section:
- [math]\frac{d \sigma}{d \epsilon_1 d \theta_1 d \theta_2} = 8 \left ( \frac{\pi a}{\sinh (\pi a)} \right )^2 \frac{a^2}{2 \pi} \frac{e^2}{\hbar c} \left ( \frac{\hbar}{m_e c }\right )^2 \frac{\epsilon_1 \epsilon_2}{k^3} \theta_1 \theta_2 [/math]
- [math]\times \left \{ \frac{V^2(x)}{q^4} \left [ k^2 (u^2 + v^2) \xi \eta - 2 \epsilon_1 \epsilon_2 (u^2 \xi^2 + v^2 \eta^2 ) + 2 (\epsilon_1^2 + \epsilon_2^2)uv \xi \eta cos(\phi) \right ] \right . [/math]
- [math]\left . + a^2W^2(x) \xi^2 \eta^2 \left [ k^2(1 - (u^2+v^2)\xi \eta - 2 \epsilon_1 \epsilon_2 (u^2 \xi^2 + v^2 \eta^2) -2 (\epsilon_1^2 + \epsilon_2^2) u v \xi \eta \cos(\phi)\right ]\right \}[/math]
where
- [math]k =[/math] photon momentum/energy
- [math]\theta_1[/math] = scattering angle of [math]e^+[/math]
- [math]\theta_2[/math] = scattering angle of [math]e^-[/math]
- [math]\phi = \phi_1 - \phi_2 = \phi[/math] angle between the [math]e^+[/math] and [math]e^-[/math] pair
- [math]\epsilon_1 = \sqrt{p_1^2 + m_e^2}[/math] = Energy of the positron
- [math]\epsilon_2 = \sqrt{p_2^2 + m_e^2}[/math] = Energy of the electron
- [math]u = \epsilon_1 \theta_1[/math]
- [math]v=\epsilon_2 \theta_2[/math]
- [math]\xi = \frac{1}{1+u^2}[/math]
- [math]\eta= \frac{1}{1+v^2}[/math]
- [math]q^2 = u^2 + v^2 + 2 u v \cos(\phi)[/math]
- [math]x= 1-q^2 \xi \eta[/math]
- [math]V(x) = 1 + \frac{a^2}{(1!)^2} + \frac{a^2 (1+a^2) x^2}{(2!)^2} + \frac{a^2 (1+a^2)(2^2+a^2)x^4 x^2}{(3!)^2} + \cdots[/math]
- [math]W(x) = \frac{1}{a^2} \frac{d V(x)}{d x}[/math]
- [math]a = \frac{Ze^2}{\hbar c}[/math]
- Note
- The above equations for the differential cross section are using "natural" units where [math]c \equiv 1[/math]
Davies' version integrates over all angles
Davies published a version which has been integrated over angles and includes some screening effects ( see Eq 35):
- [math]\frac{d \sigma}{d \epsilon_1} = 2 a^2 \frac{e^2}{\hbar c} \left ( \frac{\hbar}{m_e c }\right )^2 \frac{\epsilon_1^2 +\epsilon_2^2 + + \frac{2}{3} \epsilon_1 \epsilon_2 }{k^2} \left [ 2 \log \left (\frac{2\epsilon_1 \epsilon_2}{k^2} \right ) - 1 - 2 f(Z)\right ][/math]
- [math]= 4 Z^2 \alpha r_2^2 \frac{\epsilon_1^2 +\epsilon_2^2 + + \frac{2}{3} \epsilon_1 +\epsilon_2 }{( h \nu)^3} \left [ 2 \log \left (\frac{2\epsilon_1 \epsilon_2}{h \nu m_e c^2} \right ) - 1 - 2 f(Z)\right ][/math]
where
- [math]f(Z) = a^2 \sum_1^{\infty} \frac{1}{\nu (Z^2 +a^2)} \sim \frac{1}{1+a^2} + 0.20206 - 0.0369 a^2 + 0.0083 a^4 - 0.002 a^6[/math]
If you integrate over all positron ([math]\epsilon_1[/math] ) energies you get Eq. 44 (no screening)
- [math]\sigma_{e^+e^-} = 4 Z^2 \alpha r_e^2 \left [ \frac{7}{9} \right ( \ln(\frac{2 h \nu}{m_e c^2}) -f(Z) \left ) - \frac{763}{378} \right ][/math]
and Eq. 45 (complete screening)
- [math]\sigma_{e^+e^-} = 4 Z^2 \alpha r_e^2 \left [ \frac{7}{9} \right ( \ln(\frac{183}{Z^{\frac{1}{3}}}) -f(Z) \left ) - \frac{7}{378} \right ][/math]
Davies expressions were shown to work well at high energies ([math]E_{\gamma} \gt 88[/math] MeV)
Overbo's low energy Cross sections
At low energies ( [math]E_\gamma \lt 5[/math] MeV), Overbo published an exact calculation in the case that the Atomic field is unscreened. Overbo then provided a fit to the results of his calculation which he claims is valid to within 0.1% for the energy range [math](3 MeV \lt E_{\gamma} \lt 5 MeV)[/math]. The fit is given in Eq. 7.1 of his paper as
- [math]\sigma_{e^+e^-} = \sigma_B \left ( 1 + a + \frac{b}{k-2}\right )[/math]
where
- [math]a= -0.44 (\alpha Z)^2 - 0.07 (\alpha Z)^4[/math]
- [math]b= 5.06 (\alpha Z)^2 - 2.1 (\alpha Z)^4[/math]
- [math]\sigma_B = \alpha Z^2 r_e^2 \frac{2 \pi}{3} \left ( \frac{k-2}{k} \right ) ^3 \left [ 1 + \frac{\epsilon}{2} + \frac{23 \epsilon^2}{40} + \frac{11 \epsilon^3}{60} + \frac{29\epsilon^4}{960} \right ]=[/math] Low Energy unscreened Born approximation total cross section for pair production
- [math] k = \frac{h \nu}{m_e c^2} = \frac{E_{\gamma}}{0.511 MeV}[/math] = incident photon energy in units of the electron rest mass energy
- [math]\epsilon \equiv \frac{2k -4}{2+k+2\sqrt{2k}}[/math]
Intermediate Energy Cross sections
For [math]5 MeV \lt E_{\gamma} \lt 80 MeV[/math] the Gradstein semi-ephirical formula is used from G. White Gradstein, Natl. Bur. Standard., Circ 583 (1957) pg 1.
- [math]\sigma = \sigma_{BH} - \Delta_e + \frac{b^2}{k} \ln(k -0.57)[/math]
where
- [math]\Delta_e[/math] = empirical constant = 4.02 barns for Pb
- [math]b^2[/math] = empirical constant = 16.8 barns for Pb
- [math]\sigma_{BH}[/math] = Simulations_of_Particle_Interactions_with_Matter#Bremsstrahlung Bethe-Heitler cross section
Triplet production
- Triplet Production
- identifies photon-electron pair production. The recoiling electron track adds to the two [math]e^+e^-[/math] tracks making three total particle tracks (kind of like pair production ionization).
A description for how to calculate the cross section for this process is illustrated for 1[math]0 \lt E_{\gamma} \lt 20 MeV[/math] in L.E. Wright, Phys. Rev. C 36 (1987) pg 582. Unfortunately, analytic expression is not given but one could construct tables of [math]Tq(92)[/math] and [math]Tq(1)[/math] in equation 65 of L.E. Wright's paper.
An example for [math]E_{\gamma} =6 MeV[/math] may be found in Sud & Vargus, Phys. Rev. A49 (1994) pg 4624.
GEANT4 Pair production
GEANT4 uses the pair production cross section given in Tsai, Rev. Mod. Phys, vol 46 (1974) pg 815.
- [math]\frac{d \sigma}{d \epsilon} = Z(Z+ \eta) \alpha r_e^2 \left \{ \left [ \epsilon^2 +(1- \epsilon)^2 (\phi_1 - 4f(Z) ) \right ] + \frac{2}{3} \epsilon(1-\epsilon) (\phi_2 - 4f(Z) )\right \}[/math]
where
- [math]E_{\gamma} =[/math] energy of incident photon
- [math]E_{e^-} =[/math] KE of create electron
- [math]\epsilon = \frac{E_{e^-} +m_ec^2}{ E_{\gamma}} =[/math] fraction of [math]E_{\gamma}[/math] taken away by [math]e^-[/math]
- [math]\eta=[/math] triplet production correction
- [math]f(Z) =[/math] high energy coulomb correction from Davies above
- [math]\phi_1[/math] & [math]\phi_2[/math] = electron screening functions
The formula GEANT4 uses may also be found on pg 541 in J. Bono , Radiation Physics Chemistry, vol 44 (1994) pg 531
- [math]\frac{d \sigma}{d\epsilon} = \frac{2}{3} Z(Z+ \eta) \alpha r_e^2 C_r \left [ 2(\frac{1}{2} - \epsilon)^2 \phi_1(\epsilon) + \phi_2(\epsilon) \right ] [/math]
where
- [math]\phi_1(\epsilon) = g_1(b) + g_0(\kappa)[/math]
- [math]\phi_2(\epsilon) = g_2(b) + g_0(\kappa)[/math]
- [math]g_1(b) = \frac{2}{3} - 2 \ln(1+b^2) - 6b \tan^{-1}(\frac{1}{b} - b^2 \left [ 4 -4b\tan^{-1}(\frac{1}{b} -3 \ln(1 + \frac{1}{b^2}\right][/math]
- [math]g_2(b) = \frac{11}{6} - 2 \ln(1+b^2) - 3b \tan^{-1}(\frac{1}{b} - \frac{b^2}{2} \left [ 4 -4b\tan^{-1}(\frac{1}{b} -3 \ln(1 + \frac{1}{b^2}\right][/math]
- [math]g_0(\kappa) =4 \ln ( \frac{R m_e c}{\hbar}) + 4f(Z) + F_0(\kappa,Z)[/math]
- [math]F_0(\kappa,Z) = \left [ -0.1774 - 12.10 \alpha Z + 11.18 (\alpha Z)^2 \right ] \sqrt{\frac{2}{\kappa}} + \left [ 8.523 + 73.26 \alpha Z - 44.41(\alpha Z)^2 \right ] \frac{2}{\kappa}[/math]
- [math]- \left [ 13.52 + 121.1 \alpha Z - 96.41 (\alpha Z)^2 \right ] \left ( \frac{2}{\kappa} \right)^{2/3} + \left [ 8.946 + 62.05 \alpha Z - 63.41(\alpha Z)^2 \right ] \left ( \frac{2}{\kappa} \right )^2[/math]= low energy coulomb correction
- [math]R[/math] = screening radius (adjustable parameter)
- [math]\frac{\hbar}{m_ec} = 3.8616 \times 10^{-13} m[/math] = Compton wavelength
- [math]b = \frac{Rm_e c}{\hbar} \frac{1}{2\kappa} \frac{1}{\epsilon(1-\epsilon)}[/math]
- [math]\kappa = \frac{E_{\gamma}}{m_e c^2}[/math]
An older simulation description with graphs of the cross-sections may be found below.
File:Bigg Lighthill conversion 1Mev-100MeV SandiaPreprint SC-RR-68-619.pdf
Below is the review of Modern Physics article basically summarizing all of the physics for pair production up to 1969
File:RevModPhys PairPoduction 1969 MotzOlsonKoch.pdf
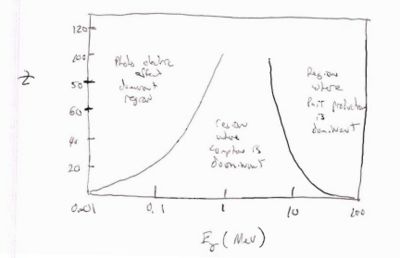
Contributions as function of Z
The plot below shows the contributions of the three photon absorption physics processes as a function of the incident photon energy and the Z of the target material.
At low energy (keV), the photo-electric effect dominant while at high energies (> 1 MeV) pair production starts to dominate. Compton scattering dominates in the intermediate energy region.
Hadronic Interactions
Proton Bremsstrahlung
- [math]\sigma_{class}|_{90^o} = 2.1\times 10^{-31} cm^2/sterad[/math] = cross section for dipole radiation emitted at 90 degrees with respect to incident beam of particles scattered in a Coulomb field.
File:ProtonBrem Drell Huang PhysRev v99 n3 1955 pg686.pdf
Pluto event generator
A ROOT based Hadronic Simulation package based on Pluto
I installed Pluto V 5.14.1 on inca
I needed to set the environmental variables under tcsh
setenv ROOTSYS ~/src/ROOT/root
setenv PATH ${PATH}:${ROOTSYS}/bin
setenv LD_LIBRARY_PATH $ROOTSYS/lib
There is a subdirectory called "macros"
cd macros
Go to that subdirectory and type root, this will run the contents of the file "rootlogin.C"
cd macros
inca:~/src/Pluto/pluto_v5.14.1/macros> root
*******************************************
* *
* W E L C O M E to R O O T *
* *
* Version 5.17/03 30 August 2007 *
* *
* You are welcome to visit our Web site *
* http://root.cern.ch *
* *
*******************************************
Compiled on 5 September 2007 for linux with thread support.
CINT/ROOT C/C++ Interpreter version 5.16.24, July 26, 2007
Type ? for help. Commands must be C++ statements.
Enclose multiple statements between { }.
*********************************************************
* The Pluto event generator
* (C) HADES collaboration and all contributing AUTHORS
* www-hades.gsi.de/computing/pluto/html/PlutoIndex.html
* Version: 5.14.1
* Compiled on 10 December 2008
*********************************************************
Shared library Pluto.so loaded
to run a pp elastic model type
root [0] .x pp_elastic.C
a root ntuple is generate called "pp_elastic.root"
you can then analyze the data in the root file with
data->MakeClass();
the above command within root generates an analysis skeleton program.
using t.Show you can see the structure of the events within the ntuple. A few functions are also stored in the root tree which you can use.
You can use the root file event to create an input file which GEANT4 can then use as its event generator. GEANT4 then reads the events in and propagates them through your geometry.
Neutron Interactions
| Name |
Energy
|
| Cold Neutron |
micro eV
|
| Thermal |
[math]\sim \frac{1}{40}[/math] eV
|
| epithermal |
[math] \frac{1}{40} eV \rightarrow 100 keV[/math]
|
| fast |
[math]100 keV \rightarrow 100 MeV[/math]
|
| high energy |
[math] \gt 100 MeV[/math]
|
Note: Interaction length for neutrons is ~[math]10^{-13}[/math] .
Neutrons are even better than photons for penetrating matter.
Elastic scattering
File:Elastic scattering from Nuclei.jpg
[math]v_{CM} = \frac{m_n v_L + M(0)}{m_n + M} = \frac{v_0}{1 + \frac{M}{m_n}} = \frac{v_0}{1+A} =[/math] velocity of CM frame
[math]{v_L}^' = [/math] Magnitude of Neutron velocity in CM frame before and after collision
[math]= v_c - v_{CM} = v_0 -\frac{v_0}{1+A} = \frac{(1+A)-1}{1+A} v_0 = \frac{A}{1+A} v_0[/math]
[math] v = [/math] Magnitude of Nucleus velocity in CM frame before and after collision
[math]= v_{CM} = \frac{v_0}{1+A}[/math]
Note: In elastic collision only the particles direction changes.
[math]\vec{v}_L = {\vec{v}_L}^' + \vec{v}_{CM}[/math]
File:Rule of cosines.jpg
- [math]c^2 = a^2 + b^2 - 2abcos \theta[/math]
[math](v_L)^2 = ({v_L}^')^2 + (v_{CM})^2 - 2 v_{CM} {v_L}^' cos(\pi - {\theta}_{CM})=[/math]
- [math]= ({v_L}^')^2 + (V)^2 - 2 V {v_L}^' cos(\pi - {\theta}_{CM})=[/math]
where
- [math]({v_L}^')^2 = (\frac{A}{1+A})^2 {v_0}^2[/math]
- [math](V)^2 = (\frac{1}{1+A})^2 {v_0}^2[/math]
After substitution we get following:
[math](\frac{v_L}{v_0})^2 = \frac{A^2 +1 - 2 A cos(\pi - {\theta}_{CM})}{(1+A)^2} = \frac{A^2 +1 + 2 A cos({\theta}_{CM})}{(1+A)^2}[/math]
[math]
cos(A+/-B) = cosAcosB -/+ sinAsinB[/math]
[math]\frac{E}{E_0} = \frac{A^2 + 1 + 2Acos({\theta}_{CM})}{(1+A)^2}[/math]
when [math]{\theta}_{CM}=0[/math], [math]E_{max} = E_0[/math].
[math]E_{min} = \frac{(A-1)^2}{(A+1)^2} E_0 = (\frac{A-1}{A+1}) E_0 =[/math] Minimum energy of scattered Neutron in LAB frame.
File:Rule of cosines 1.jpg
[math]({v_L}^')^2 = (v_L)^2 + (v_{CM})^2 - 2 v_{CM} v_L cos(\pi - {\theta}_{CM})=[/math]
- [math]= (v_L)^2 + (V)^2 - 2 V v_L cos({\theta}_{L})=[/math]
[math](\frac{Av_0}{1+A})^2 = {v_L}^2 + (\frac{v_0}{1+A})^2 - 2 v_L (\frac{v_0}{1+A}) cos({\theta}_L)[/math]
After substituting [math]v_L[/math]
[math]cos{\theta}_L = [\frac{A^2 + 1 + 2 A cos{\theta}_{CM}}{(1+A)^2} + (\frac{1}{1+A})^2 - (\frac{A}{1+A})^2] \times \frac{(1+A)^2}{2\sqrt{A^2 +1 + 2Acos{\theta}_{CM}}} = [/math]
[math]= \frac{[A^2 +1 + 2Acos{\theta}_{CM} + 1 - A^2]}{2\sqrt{A^2 +1 + 2Acos{\theta}_{CM}}} = \frac{1 + Acos{\theta}_{CM}}{\sqrt{A^2 +1 + 2Acos{\theta}_{CM}}}
[/math]
Note: [math] {E_A}^{CM} = \frac{1}{2} M_A V^2 = \frac{1}{2} A m_n (\frac{v_0}{1+A})^2 = \frac{A}{(1+A)^2} \frac{m_n {v_0}^2}{2}= [/math]
[math] = \frac{A}{(1+A)^2}E_0 = [/math] Energy of recoil Nuclei in CM frame.
Conservation of Energy: [math]E_0 = E + E_A[/math]
- [math] E_A = E_0 - E = E_0 - \frac{A^2 + 1 + 2Acos{\theta}_{CM}}{(1+A)^2} E_0 = [/math]
- [math]\frac{(1+A)^2 - (A^2 +1 + 2Acos{\theta}_{CM})}{(1+A)^2}E_0 =[/math]
Inelastic Scattering
Resources
GEANT4 Home Page
ROOT Home page
Fermi Lab Example
NIST Range Tables
X-ray specturm
Installing_GEANT4.9.3_Fsim
Building GEANT4.9.5
TF_GEANT4.9.5
TF_SPIM_OLD