Neutron Polarimeter

Go Back

Four-vector Algebra

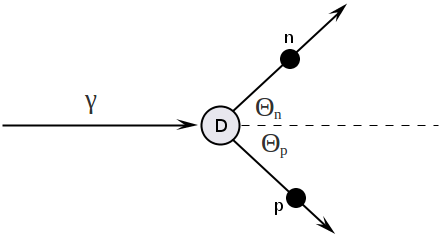
Consider two bode reaction [math]D(\gamma, n)p[/math]:

Write down four-momentum vectors before and after reaction:

[math] p_{\gamma} = \left( T_{\gamma},\ T_{\gamma},\ 0,\ 0  \right) [/math] 
[math] p_D     = \left( m_D,\ 0,\ 0,\ 0  \right) [/math] 
[math] p_{n} = \left( E_n,\ \ p_n\cos \Theta_n,\ \ p_n\sin \Theta_n,\ \ 0  \right) [/math] 
[math] p_{p} = \left( E_p,\ \ p_p\cos \Theta_p,\ \ p_p\sin \Theta_p,\ \ 0  \right) [/math] 

Now apply the law of conservation of four-momentum vectors:

[math] p^{\mu}_{\gamma} + p^{\mu}_D = p^{\mu}_p + p^{\mu}_n\ \ \Rightarrow \ \  p^{\mu}_p = p^{\mu}_{\gamma} + p^{\mu}_D - p^{\mu}_n[/math]

Squaring both side of equation above and using the four-momentum invariants [math](p^{\mu})^2 = m^2[/math] we have:

[math] m_p^2 = m_D^2 + m_n^2 +  2T_{\gamma}\cdot m_D  - 2m_D\cdot E_n - 2\left( T_{\gamma}E_n - T_{\gamma}p_n\cos\Theta_n\right) [/math]

Detector located at [math]\Theta = 90^o[/math] case

Detector is located at [math]\Theta_n = 90^o[/math], and the formula above is simplified:

[math] m_p^2 = m_D^2 + m_n^2 +  2\ T_{\gamma}\cdot m_D  - 2\ m_D\cdot E_n - 2\ T_{\gamma}E_n [/math]

We can easily solve the equation above with respect to incident photon energy:

[math]T_{\gamma} = \frac {m_p^2 - m_n^2 - m_D^2 + 2\ m_D E_n}{2\ (m_D - E_n)}
                  = \frac {m_p^2 - m_n^2 - m_D^2 + 2\ m_D (T_n+m_n)}{2\ (m_D - (T_n+m_n))} [/math]

For non-relativistic neutrons [math]T_n \ll m_n = 939.5\ MeV[/math] and the formula above is become:

[math]T_{\gamma} = \frac {m_p^2 - m_n^2 - m_D^2 + 2\ m_D m_n + 2\ m_D T_n}{2\ (m_D - m_n)} [/math]

Substituting the corresponding masses, we get finally:

[math]T_{\gamma}\ [MeV] = 2.003\ T_n\ [MeV] + 1.715\ [MeV]\ \ \ \ [1][/math]

and visa versa:

[math]T_n\ [MeV] = 0.499\cdot T_{\gamma}\ [MeV] - 0.856\ [MeV]\ \ \ \ [2][/math]

Here I derived the formula [2] just inversing the formula [1]. I can as well start from exact solution above, solve this equation with respect to neutron energy, do the non-relativistic approximation and get exactly the same formula [2]. But anyway we ended up with two useful non-relativistic formulas we can analyze now:

1) from formula [1] above we can predict the threshold of [math]^2D(\gamma, n)[/math] reaction in [math]\Theta_n = 90^o[/math] direction:

[math]E_{\gamma} = 1.715\ MeV[/math]

comment: it's not true because by momentum conservation there are no neutron with zero kinetic energy.

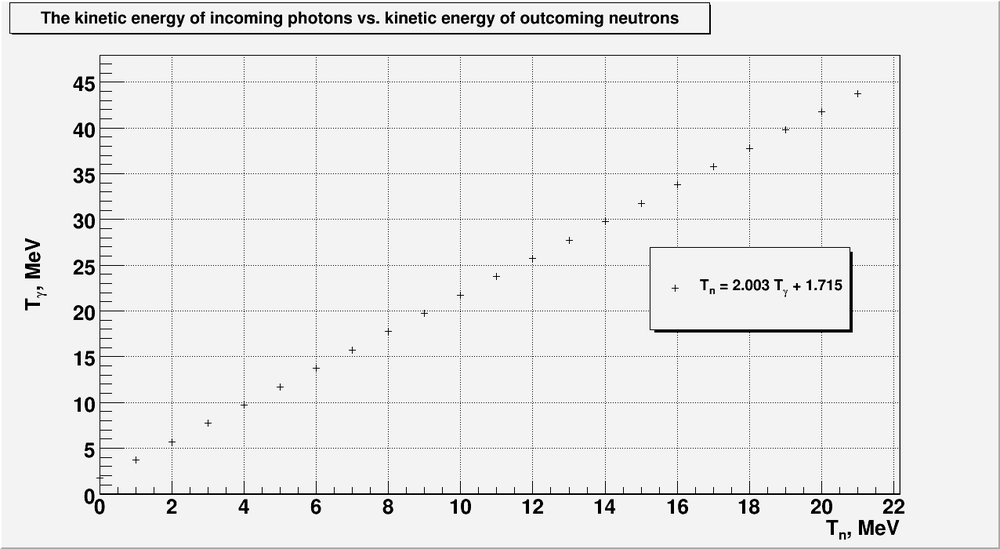
2) from formula [1] above we can predict the incident photon energy based on the detected neutron energy (neutron polarimeter).

3) from formula [2] above we can predict the detected neutron energy based on the incident photon energy.

 -  for the incident photons up to [math]25\ MeV[/math] we can detect neutrons up to  [math]11.62\ MeV[/math]

 -  for the incident photons up to [math]44\ MeV[/math] we can detect neutrons up to  [math]21.10\ MeV[/math]

4) we can do the error calculations.

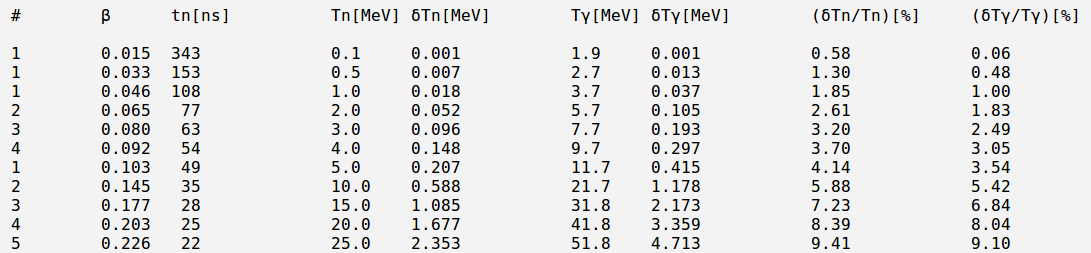
Example of error calculation

example 1

Say, we have, 10 MeV neutron with uncertainty 1 MeV, the corresponding uncertainly for photons energy is:

[math] \delta T_{\gamma} = 2.003\ \delta T_n = 2.003\times 1\ MeV = 2.003\ MeV [/math]

example 2

In the calculations below I attempted to predict the uncertainty in photons energy based on uncertainty in neutrons time of flight.

The neutron kinetic energy as function of time of flight is:

[math]T_n = m_n (\gamma - 1) = m_n\left[ \frac{1}{\sqrt{1-\left(\frac{l}{c\ t}\right)^2}} - 1 \right][/math]

By taking derivative of the expression above we can find the relative error for neutron energy:

[math]\delta T_n \left(\delta t\right) = -\ \frac{m\ l^2}{\left(1-\left(\frac{l}{c\ t}\right)^2\right)^{3/2}c^2 t^3} \cdot  \delta t[/math]

In that formula for [math]\delta T_n[/math] we need to know the neutron time of flight which is:

[math]t:=\frac{l}{c\ \beta_n} = \frac{l}{c\ (p_n/E_n)} =
         \frac{l\ (T_n + m_n)}{c\sqrt{T_n^2+2m_nT_n}}[/math]

And now we can calculate the relative error for photon energy using the formula derived before:

[math]\delta T_{\gamma} = 2.003\ \delta T_n[/math]

Say, the detector is 1.5 m away and neutron's time of flight uncertainty is:

[math]\delta t = 1\ ns[/math]

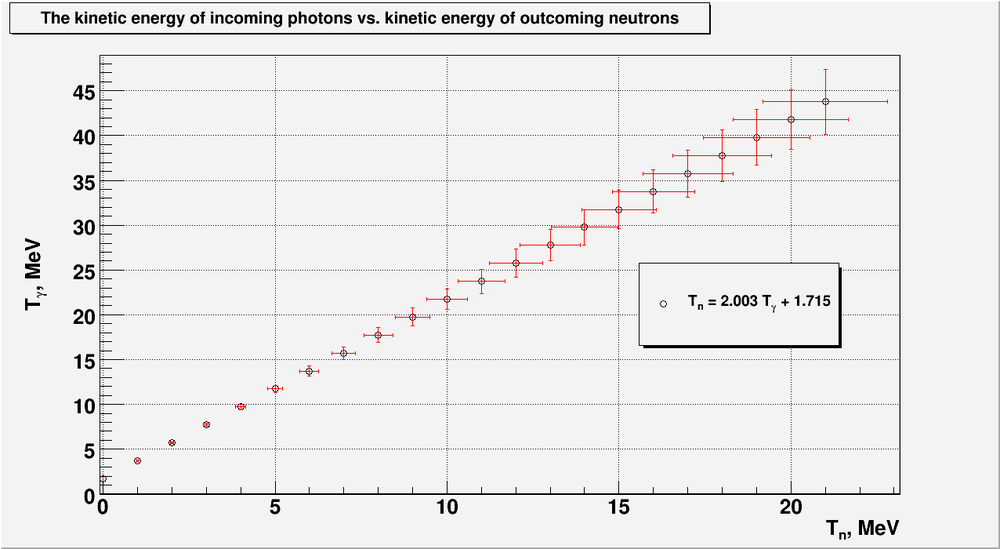
In the table below are presented some calculation results using the formulas above:

And in the plot below I have overlay my error calculations using the formulas above:

[math]\Theta[/math] dependence

Starting from general kinematic relations:

[math] m_p^2 = m_D^2 + m_n^2 +  2T_{\gamma}\cdot m_D  - 2m_D\cdot E_n - 2\left( T_{\gamma}E_n - T_{\gamma}p_n\cos\Theta_n\right) [/math]

we can solve the equation above with respect to [math]T_{\gamma}[/math] as function of neutron energy [math]T_n[/math] and neutron angle [math]\Theta_n[/math]

[math]T_{\gamma} = \frac{m_p^2-m_n^2-m_D^2+2m_D E_n}{2(m_D-E_n-p_n\cos\Theta_n)}[/math]

and using

[math]E_n = T_n+m_n[/math]
[math]p_n = \sqrt{E_n^2-m_n^2} = \sqrt{T_n^2+2T_n m_n^2}[/math]

finally

[math]T_{\gamma} = \frac{m_p^2-m_n^2-m_D^2+2m_D (T_n+m_n)}{2\left(m_D-m_n-T_n-(\sqrt{T_n^2+2T_n m_n^2})\cos\Theta_n\right)}[/math]

Go Back