|
|
| Line 108: |
Line 108: |
| | | | |
| | | | |
| − | [[File:Error table01.png | 1000 px]] | + | [[File:Error table01.png | 1200 px]] |
| − | | |
| − | {| height="10" border="1" cellpadding="15" cellspacing="0"
| |
| − | |-
| |
| − | |<math>\delta t_n</math>
| |
| − | |<math>l</math>
| |
| − | |<math>T_n</math>
| |
| − | |<math>\beta_n</math>
| |
| − | |<math>t_n</math>
| |
| − | |<math>\delta T_n</math>
| |
| − | |<math>\frac{\delta T_n}{T_n}</math>
| |
| − | |<math>\delta T_{\gamma}</math>
| |
| − | |<math>\frac{\delta T_{\gamma}}{T_{\gamma}}</math>
| |
| − | |-
| |
| − | |1 ns||1.5 m||0.1 MeV||0.015||343 ns||0.0006 MeV||0.6 %||0.0012 MeV||0.06 %
| |
| − | |-
| |
| − | |1 ns||1.5 m||0.5 MeV||0.033||153 ns||0.006 MeV||1.3 %||0.013 MeV||0.5 %
| |
| − | |-
| |
| − | |1 ns||1.5 m||1.0 MeV||0.046||108 ns||0.02 MeV||1.9 %||0.04 MeV||1.0 %
| |
| − | |-
| |
| − | |1 ns||1.5 m||2.0 MeV||0.065||77 ns||0.05 MeV||2.6 %||0.11 MeV||1.8 %
| |
| − | |-
| |
| − | |1 ns||1.5 m||5.0 MeV||0.103||49 ns||0.21 MeV||4.1 %||0.41 MeV||3.5 %
| |
| − | |-
| |
| − | |1 ns||1.5 m||10.0 MeV||0.145||35 ns||0.59 MeV||5.9 %||1.18 MeV||5.4 %
| |
| − | |-
| |
| − | |1 ns||1.5 m||20.0 MeV||0.203||25 ns||1.68 MeV||8.4 %||3.36 MeV||8.0 %
| |
| − | |}
| |
| | | | |
| | | | |
Go Back
Four-vector Algebra
Consider two bode reaction [math]D(\gamma, n)p[/math]:
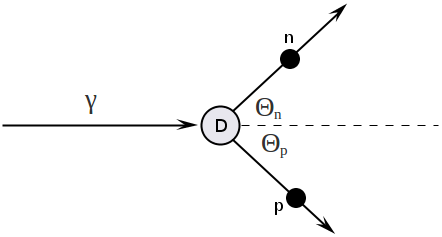
Write down four-momentum vectors before and after reaction:
[math] p_{\gamma} = \left( T_{\gamma},\ T_{\gamma},\ 0,\ 0 \right) [/math]
[math] p_D = \left( m_D,\ 0,\ 0,\ 0 \right) [/math]
[math] p_{n} = \left( E_n,\ \ p_n\cos \Theta_n,\ \ p_n\sin \Theta_n,\ \ 0 \right) [/math]
[math] p_{p} = \left( E_p,\ \ p_p\cos \Theta_p,\ \ p_p\sin \Theta_p,\ \ 0 \right) [/math]
Now apply the law of conservation of four-momentum vectors:
[math] p^{\mu}_{\gamma} + p^{\mu}_D = p^{\mu}_p + p^{\mu}_n\ \ \Rightarrow \ \ p^{\mu}_p = p^{\mu}_{\gamma} + p^{\mu}_D - p^{\mu}_n[/math]
Squaring both side of equation above and using the four-momentum invariants [math](p^{\mu})^2 = m^2[/math] we have:
[math] m_p^2 = m_D^2 + m_n^2 + 2T_{\gamma}\cdot m_D - 2m_D\cdot E_n - 2\left( T_{\gamma}E_n - T_{\gamma}p_n\cos\Theta_n\right) [/math]
Detector located at [math]\Theta = 90^o[/math] case
Detector is located at [math]\Theta_n = 90^o[/math], and the formula above is simplified:
[math] m_p^2 = m_D^2 + m_n^2 + 2\ T_{\gamma}\cdot m_D - 2\ m_D\cdot E_n - 2\ T_{\gamma}E_n [/math]
We can easily solve the equation above with respect to incident photon energy:
[math]T_{\gamma} = \frac {m_p^2 - m_n^2 - m_D^2 + 2\ m_D E_n}{2\ (m_D - E_n)}
= \frac {m_p^2 - m_n^2 - m_D^2 + 2\ m_D (T_n+m_n)}{2\ (m_D - (T_n+m_n))} [/math]
For non-relativistic neutrons [math]T_n \ll m_n = 939.5\ MeV[/math] and the formula above is become:
[math]T_{\gamma} = \frac {m_p^2 - m_n^2 - m_D^2 + 2\ m_D m_n + 2\ m_D T_n}{2\ (m_D - m_n)} [/math]
Substituting the corresponding masses, we get finally:
[math]T_{\gamma}\ [MeV] = 2.003\ T_n\ [MeV] + 1.715\ [MeV]\ \ \ \ [1][/math]
and visa versa:
[math]T_n\ [MeV] = 0.499\cdot T_{\gamma}\ [MeV] - 0.856\ [MeV]\ \ \ \ [2][/math]
Here I derived the formula [2] just inversing the formula [1]. I can as well start from exact solution above, solve this equation with respect to neutron energy, do the non-relativistic approximation and get exactly the same formula [2]. But anyway we ended up with two useful non-relativistic formulas we can analyze now:
1) from formula [1] above we can predict the threshold of [math]^2D(n,\gamma)[/math] reaction in [math]\Theta_n = 90^o[/math] direction:
[math]E_{\gamma} = 1.715\ MeV[/math]
2) from formula [1] above we can predict the incident photon energy based on the detected neutron energy (neutron polarimeter).
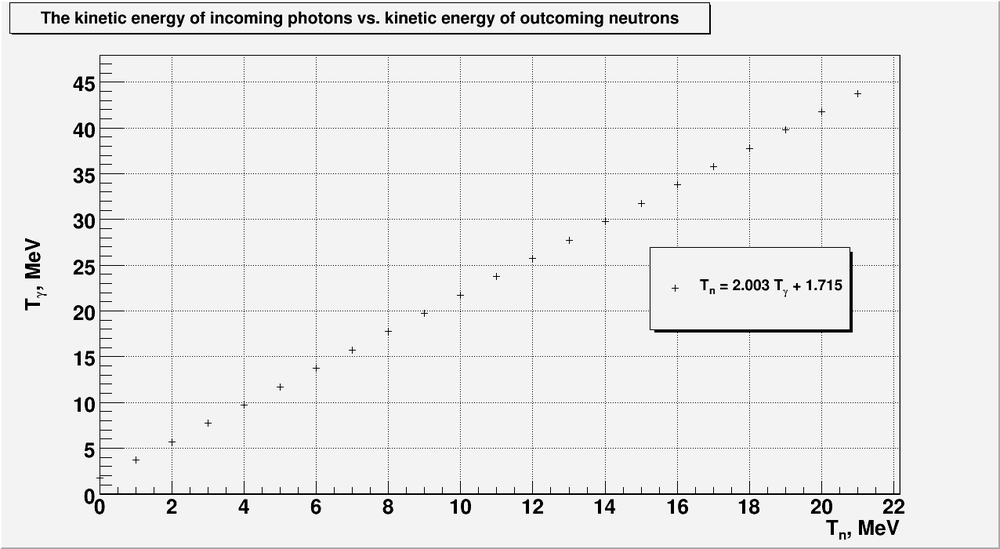
3) from formula [2] above we can predict the detected neutron energy based on the incident photon energy.
- for the incident photons up to [math]25\ MeV[/math] we can detect neutrons up to [math]11.62\ MeV[/math]
- for the incident photons up to [math]44\ MeV[/math] we can detect neutrons up to [math]21.10\ MeV[/math]
4) we can do the error calculations.
Example of error calculation
example 1
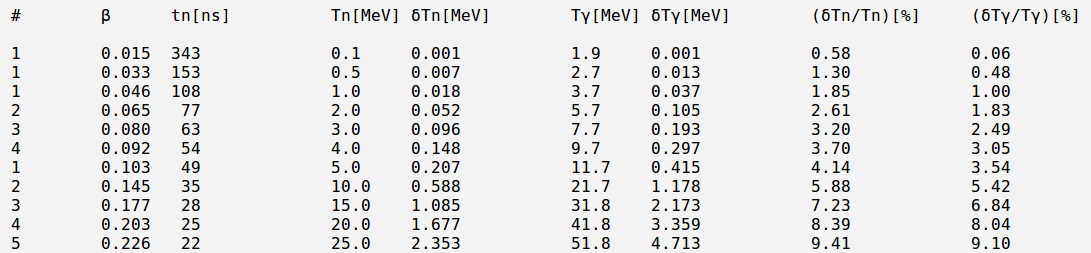
Say, we have, 10 MeV neutron with uncertainty 1 MeV,
the corresponding uncertainly for photons energy is:
[math] \delta T_{\gamma} = 2.003\ \delta T_n = 2.003\times 1\ MeV = 2.003\ MeV [/math]
example 2
In the calculations below I attempted to predict the uncertainty in photons energy based on uncertainly of neutrons time of flight.
Say, the neutron's time of flight uncertainty is:
[math]\delta t = 1\ ns[/math]
The neutron kinetic energy is:
[math]T_n = m_n (\gamma - 1) = m_n\left[ \frac{1}{\sqrt{1-\left(\frac{l}{c\ t}\right)^2}} - 1 \right][/math]
By taking derivative of the expression above we can find the relative neutron energy error:
[math]\delta T_n \left(\delta t\right) = -\ \frac{m\ l^2}{\left(1-\left(\frac{l}{c\ t}\right)^2\right)^{3/2}c^2 t^3} \cdot \delta t[/math]
Also we need to know the neutron time of flight as function of the neutron energy:
[math]t:=\frac{l}{c\ \beta_n} = \frac{l}{c\ (p_n/E_n)} =
\frac{l\ (T_n + m_n)}{c\sqrt{T_n^2+2m_nT_n}}[/math]
Say, we have 10 MeV neutron, 1.5 m away detector, and neutron's time of flight uncertainty is [math]1\ ns[/math]. And below are some error calculations using the formulas above:
Go Back


