TF EIM Chapt6

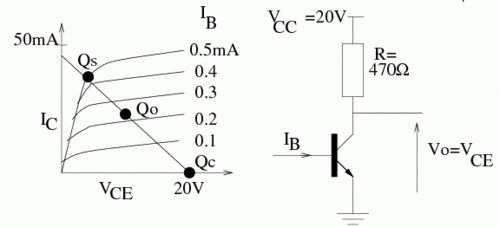
Load Line

The load line represents the bias conditions in which the [math]I_C -vs V_{CE}[/math] dependence is linear;(i.e.: a constance Resistance). Setting up a circuit which changes the transistor bias along the load line means that the transistor is behaving like a resistor.

Consider the collector-Emitter side of the transistor below.

Kirchoff's loops theorem is

[math]V_{CC} - I_CR_C -V_{CE} = 0[/math]

[math]\Rightarrow[/math]

[math]I_C = \frac{V_{CC}}{R_C} - \frac{1}{R_C} V_{CE}[/math]

A graph of [math]I_C -vs- V_{CE}[/math] is a line with a slope of[math] - \frac{1}{R_C}[/math] and a y-intercept of [math]\frac{V_{CC}}{R_C}[/math].

If [math]I_C=0[/math] then [math]V_{CE} = V_{CC}[/math].

The point Q_0 in the above curve represents a "Quiescent" (quiet) point where the best amplification occurs because it is in the middle of the operating point. If you are designing an AC amplifier you will want to be at this point to have a wide amplifier range.

If you want to use the transistor for an analog signal (microphone-speaker) then you will want to operate the circuit near Q_0 and have a shallow load line.

Q_0 is the cutoff point where there is no output:ie; the base current is zero; the transistor has infinite resistance

Q_S is the point where the amplifier is saturating. The transistor is supplying its max current a signal going beyond will essentially be clipped. The transistor has an effective resistance of zero at this point.

If you want to make a digital switch then you want the load line as steep as possible so the circuit changes from Q_0 (off) to Q_S(on) as fast as possible.

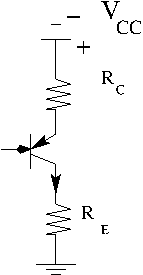
Temperature Dependence

As the temperature increases the impurity atoms tend to diffuse through the semiconductor fro high concentration regions to low concentration regions.

This diffusion changes the[math] I_C -vs- V_{CE}[/math] curve near the saturation region because the diode biasing voltages change.

You don't want the temperature change of the transistor to change the bias conditions of the transistor.

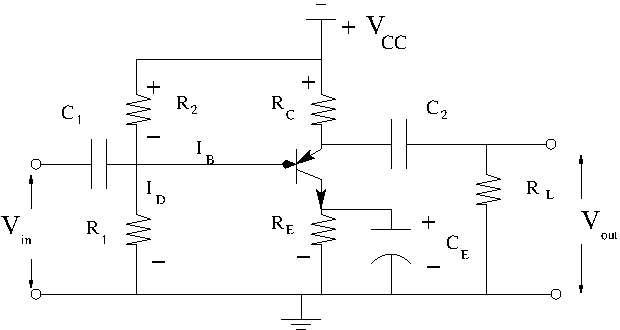
Bipolar Transistor Amplifier

A npn bipolar transistor amplifier configured with a common emitter is shown below.

Let's look at this circuit in pieces.

Starting with the above load line circuit that has been stabilized for temperature.

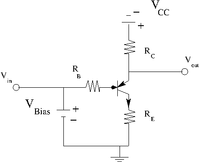
Let's add an input current for the base.

In the above circuit there is a DC bias voltage and an AC input. (The pulse generator in your lab has a DC offset you can use with the AC output sine wave).

In you lab you will want to set an[math] I_B[/math] using the DC bias [math]V_{bias}[/math] and a [math]V_{CC}[/math] in order to put you in the middle of a load line. The AC input will move along that load line.

Consider the above circuit.

Observations

1.) Notice the input goes through a high pass filter with a break point of[math] \frac{1}{R_1 C_1}[/math].

2.) The output also goes through a high pass filter with a break point of[math] \frac{1}{R_l C_2}[/math].

3.) Kirchoff voltage rule

[math]V_{CC} -I_C R_C - V_{CE} - I_E R_E = 0[/math]

[math]V_{CC} - V_{CE} -I_C (R_C + R_E) = 0[/math] [math]I_C \approx I_E[/math]

[math]\Rightarrow I_C =\frac{ V_{CC} - V_{CE}}{R_C + R_E }[/math]

4.) Kirchoff law

[math]V_{CC} -(I_B + I_D) R_2 - V_{EB} - I_E R_E = 0[/math]

5.) INput resistance

[math]\frac{1}{R_{in}} = \frac{1}{X_B} + \frac{1}{R_1} + \frac{1}{R_2}[/math]

6.)

[math]V_B = \frac{R_1}{R_1+R_2} V_{CC}[/math]

Forest_Electronic_Instrumentation_and_Measurement