Kicker Magnets

Kicker Magnet Calculations

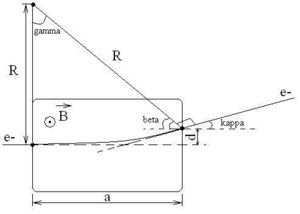
Field needed to bend 44 MeV electrons 0.47 degrees

[math]1 MeV = 1.6\cdot 10^{-13} J = 1.6\cdot 10^{-13} \frac{m^2\cdot kg}{s^2}[/math]

[math]c = 2.998 \cdot 10^8 \frac{m}{s}[/math]

[math]\frac{MeV}{C} = 0.534 \cdot 10^{-21} \frac{m\cdot kg}{s}[/math]

[math]p_e = 44 \frac{MeV}{c} = 23.5 \cdot 10^{-21} \frac{m\cdot kg}{s}[/math]

[math]B = \frac{p_e}{q_e \cdot R}[/math]

[math]1T=\frac{kg}{C\cdot s}[/math], [math]q_e = 1.6\cdot 10^{-19} C[/math], [math]1T=10^{-4}G[/math]

[math]B(T) = \frac{p_e (\frac{MeV}{c})\cdot 0.33\cdot 10^{-2}}{R(m)}[/math]

[math]B(T) = \frac{4.67\cdot 10^{-2}}{R(m)}[/math]

[math]180^0 = \kappa + 90^0 + \beta[/math]

[math]180^0 = \gamma + 90^0+ \beta[/math]

[math]\kappa = \gamma[/math]

[math]R = \frac{a}{cos(\beta)} = \frac{a}{cos(90^0 - \kappa)} = \frac{a}{sin(\kappa)}[/math]

[math]d = R \cdot (1 - cos(\kappa)) = \frac{a \cdot (1 - cos(\kappa))}{sin(\kappa)}[/math]

[math]B(T) = \frac{p_e (\frac{MeV}{c})\cdot 0.33\cdot 10^{-2}\cdot sin(\kappa)}{a(m)}[/math] - general expression for B-field.

[math]B(T) = \frac{7.83\cdot 10^{-2}\cdot sin(\kappa)}{a(m)}[/math]

If [math]\kappa = 0.47^0[/math] then [math]sin(\kappa) = 0.0082[/math] and our B-field becomes:

[math]B(T) = \frac{1.2\cdot 10^{-3}}{a(m)}[/math]

[math]a \simeq 0.125 m[/math] for the coils under consideration. Hence, the B-field needed is:

[math]B = 0.00964 T = 96.4 G[/math]

Magnetic Field Produced by Coils

300px

Assuming the coils we are using are in a solenoidal shape, we see that:

[math]z'=L+z[/math]

[math]z=z'-L[/math]

[math] B_z^n = \frac {\mu_0}{2} \int^{z}_0 \frac{R^2 I}{(a^2+R^2)^{3/2}}\,da[/math]

which gives us

[math]B_z = \frac{\mu_0 R^2 I}{2}\cdot \frac{1}{((z'-L)^2+R^2)^{3/2}}[/math]

These coils consist of 11 turns of which each turn is two deep. Furthermore, we have an inner and an outer radius [math]R[/math]. The above magnetic field can be found for both the inner and the outer layer of the coil for each turn of the coil. The maximum current these coils can handle (according to IAC personnel) is 100 Amps. Listed below is the data calculated for 100 Amps.

Coil Number	Distance from Beam Pipe	Distance from Center of Beam Pipe	B-Field (inner)	B-Field (outer)
1	0 cm	2.5 cm	0.00094392 T	0.00097 T
2	0 cm	2.5 cm	0.00094392 T	0.00097 T
3	0 cm	2.5 cm	0.00094392 T	0.00097 T
4	0 cm	2.5 cm	0.00094392 T	0.00097 T
5	0 cm	2.5 cm	0.00094392 T	0.00097 T
6	0 cm	2.5 cm	0.00094392 T	0.00097 T
7	0 cm	2.5 cm	0.00094392 T	0.00097 T
8	0 cm	2.5 cm	0.00094392 T	0.00097 T
9	0 cm	2.5 cm	0.00094392 T	0.00097 T
10	0 cm	2.5 cm	0.00094392 T	0.00097 T
11	0 cm	2.5 cm	0.00094392 T	0.00097 T

Go Back