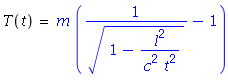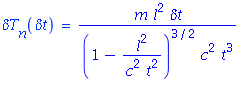Neutron Polarimeter

Go Back

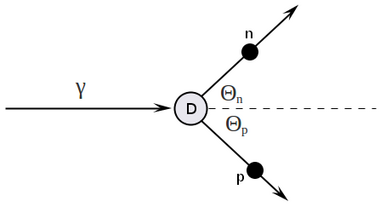
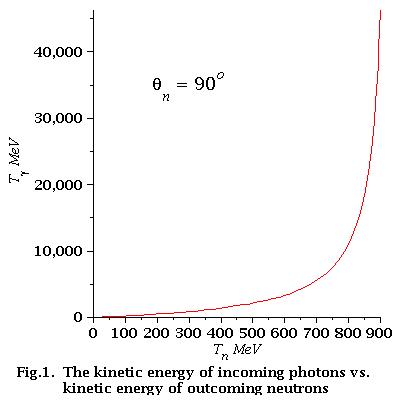
Analysis of energy dependence [math]T_{\gamma}\left( T_n\right)[/math]

four-vectors algebra

[math] E = T + m[/math]
[math] E = p^2 + m^2[/math]

writing four-vectors:

[math] p_{\gamma} = \left( T_{\gamma},\ T_{\gamma},\ 0,\ 0  \right) [/math] 
[math] p_D     = \left( m_D,\ 0,\ 0,\ 0  \right) [/math] 
[math] p_{n} = \left( E_n,\ p_n\cos(\Theta_n),\ p_n\sin(\Theta_n),\ 0  \right) [/math] 
[math] p_{p} = \left( E_p,\ p_p\cos(\Theta_p),\ p_p\sin(\Theta_p),\ 0  \right) [/math] 

Doing four-vector algebra:

[math] p^{\mu}_{\gamma} + p^{\mu}_D = p^{\mu}_p + p^{\mu}_n \Rightarrow [/math]

[math] p^{\mu\ 2}_p = \left(p^{\mu}_{\gamma} + p^{\mu}_D - p^{\mu}_n\right)^2 = 

 p^{\mu\ 2}_{\gamma} + p^{\mu\ 2}_D + p^{\mu\ 2}_n + 

    2\ p^{\mu}_{\gamma}\ p^{\mu}_D - 2\ p^{\mu}_{\gamma}\ p^{\mu}_n - 2\ p^{\mu}_D\ p^{\mu}_n [/math]

[math] m_p^2 - m_{\gamma}^2(=0) - m_D^2 - m_n^2 = [/math]

    [math] = 2\ T_{\gamma}\ m_D - 2\left( T_{\gamma}\ E_n - T_{\gamma}\ p_n\cos(\Theta_n)\right) - 2\ m_D\ E_n  [/math] 

    [math] = 2\ T_{\gamma}\left( m_D - E_n + p_n\cos(\Theta_n) \right) - 2\ m_D\ E_n [/math]

Detector is located at [math]\Theta_n = 90^o[/math], so

[math] T_{\gamma} = \frac {2\ m_D\ E_n + m_p^2 - m_D^2 - m_n^2} {2\left( m_D - E_n \right)} =
                     \frac {2\ m_D\ (T_n + m_n) + m_p^2 - m_D^2 - m_n^2} {2\left( m_D - (T_n + m_n) \right)}[/math]

and visa versa

 [math] T_n = \frac {2\ T_{\gamma}\ m_D + m_D^2 + m_n^2 - m_p^2} {2\left( T_{\gamma} + m_D \right)} - m_n[/math]

how it looks

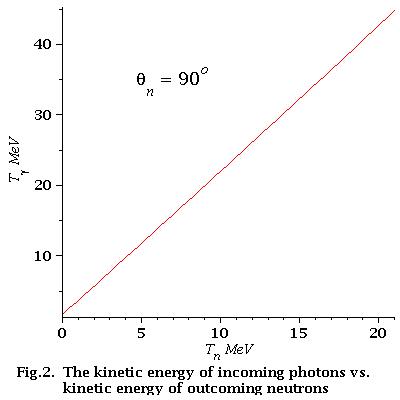
low energy approximation

As we can see from Fig.2 for low energy neutrons (0-21 MeV)

energy dependence of incident photons is linear

Find that dependence. We have:

[math] T_{\gamma}(0\ MeV) = 1.715360792\ MeV [/math]
[math] T_{\gamma}(21\ MeV) = 44.78703086\ MeV [/math]

So, the equation of the line is:

[math] T_{\gamma}
      = \frac{T_{\gamma}(21\ MeV) - T_{\gamma}(0\ MeV)}{21\ MeV - 0\ MeV}\ T_n + T_{\gamma}(0\ MeV) [/math]

Finally for low energy neutrons (0-21 MeV):

[math] T_{\gamma} = 2.051\ T_n + 1.715 [/math]

example of error analysis

example 1

Say, we have, 10 MeV neutron with uncertainty 1 MeV, the corresponding uncertainly for photons energy is:

[math] \delta T_{\gamma} = 2.051\ \delta T_n = 2.051\times 1\ MeV = 2.051\ MeV [/math]

example 2

Say, we have, 1 meter away detector with 1 ns time of flight neutron uncertainly

After some works:

And it follows:

Now say we have 10 MeV neutron. The corresponding time of flight is:

[math]t:=\frac{l}{c\ \beta} = \frac{l\ E}{c\ p} =
         \frac{l\ (T+m)}{c\sqrt{T^2+2mT}} = 23\ ns[/math]

So neutron uncertainty is:

absolute:

[math]\delta T_n(\delta t = 1\ ns,\ t=23\ ns,\ l=1\ m) = 0.88\ MeV[/math]

relative:

\frac{\delta T_n}{T_n} = 9%</math>

Corresponding photon uncertainty is:

absolute:

[math]\delta T_{gamma}
 

 relative:\lt br\gt 
 \lt math\gt \frac{\delta T_{\gamma}}{T_{gamma}} = \frac{\delta T_n}{T_n} = 9%[/math]

[math]\frac{\delta T_{\gamma}}{T_{gamma}} = \frac{\delta T_n}{T_n} = 9%[/math]

Go Back