Difference between revisions of "Forest ModernPhysics"
Jump to navigation
Jump to search
| Line 38: | Line 38: | ||
<math>p_{X-ray} = \frac{h}{\lambda} = \frac{6.63 \times 10^{-34} \mbox{ J} \cdot \mbox{s}}{7.1 \times 10^{-11}\mbox{m}} \frac{1 \mbox{eV}}{1.6 \times 10^{-19} \mbox{J}}</math> | <math>p_{X-ray} = \frac{h}{\lambda} = \frac{6.63 \times 10^{-34} \mbox{ J} \cdot \mbox{s}}{7.1 \times 10^{-11}\mbox{m}} \frac{1 \mbox{eV}}{1.6 \times 10^{-19} \mbox{J}}</math> | ||
| − | = \frac{3 \times 10^{8}\mbox{m/s}}{c} | + | <math>= 8.5 \times 10^{-15} \frac{3 \times 10^{8}\mbox{m/s}}{c}</math> |
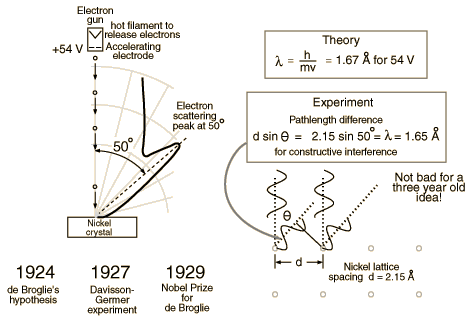
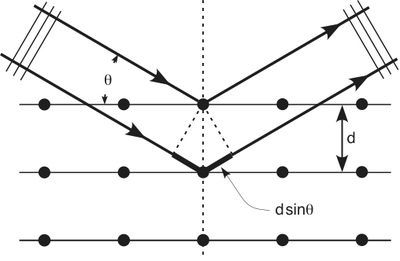
Hit a crystal made of nickel with 54 eV electrons. | Hit a crystal made of nickel with 54 eV electrons. | ||
Revision as of 01:38, 30 September 2009
Matter Waves (Wave Particle Duality)
Special relativity said that
if m=0
Plank said he could fit the Black Body radiation data assuming that that
where = Plank's constant
Combining the two we have
photons have momentum like a particle (mv)
Do particles reciprocate and behave like photons?
De Broglie's Hypothesis
If photons can behave like particles by having momentum
Then can a particle behave like a wave by having wavelength
or
de Broglie Hypothesis
Davisson and Germer
We know that X-rays having a wavelength of make an interference patter on an aluminum foil.
Hit a crystal made of nickel with 54 eV electrons.
1.) 54 eV electrons
From hyperphysics: