Difference between revisions of "HRRL radiation tests"
| Line 164: | Line 164: | ||
[[File:10MeV_Chan17.png | 200 px]] | [[File:10MeV_Chan17.png | 200 px]] | ||
| + | |||
| + | =Channel 17 Dose Estimation in New Position= | ||
| + | |||
| + | Channel 17 is a dose measuring detector on in the HRRL experimental cell. | ||
| + | |||
| + | ==1.Calculating number of particles per second == | ||
| + | |||
| + | We have electron beam of: | ||
| + | |||
| + | Frequency: f (HZ) | ||
| + | |||
| + | Peak current: I (mAmp) | ||
| + | |||
| + | Pulse width:<math> ∆t= 1 ns=1*10^(-9)<math> seconds | ||
| + | |||
| + | So, how many electrons we have in each second? | ||
| + | |||
| + | By Q=It, we have | ||
| + | |||
| + | N*e=f*I*∆t | ||
| + | |||
| + | Where Ne is the total electron numbers hits target per second, e is electron charge and f, I and ∆t are given above. | ||
| + | So | ||
| + | |||
| + | N= f*I*∆t/e=1000*0.01*5*10-8/(1.6*10-19)=3.12075*1012 | ||
| + | |||
| + | So, we have around 3.12075*1012 electrons hit radiator per second. | ||
Revision as of 12:58, 21 May 2010
Building a new positron beamline in the HRRL cell might require moving the linac itself. To help assess whether this is feasible with current shielding, radiation levels were measured on Feb 4, 2009 by M. Balzer and G. Stancari.
The HRRL was set at 15 MeV beam energy, 20 mA peak current, 1 kHz repetition rate, and 30 ns pulse width. Five OSL dosimeters were placed at each of 15 locations in the cell. Locations are marked on the following map:
Media:dosimeter-locations-20090204.pdf
Readings in mrad are reported in the following table. They were taken before exposure (first column) and after a couple of minutes of machine tuning (second column). Readings in the third column were taken 94 minutes after the second reading. During these 94 minutes, the machine was running with the settings mentioned above.
Media:exposure-measurements-20090204.pdf
Dose rates in mrad/hr at each of the 15 locations can be estimated by subtracting column 2 from column 3, averaging over the 5 dosimeters, and multiplying the result by (60 min/hr) / (94 min). RMS spreads refer to variations within each group of 5.
| Location | Dose rate | RMS spread |
|---|---|---|
| (mrad/hr) | (mrad/hr) | |
| 1 | 9 | 4 |
| 2 | 396 | 57 |
| 3 | 7940 | 204 |
| 4 | 2831 | 117 |
| 5 | 4408 | 373 |
| 6 | 29339 | 3332 |
| 7 | 72517 | 687 |
| 8 | 36507 | 4746 |
| 9 | 5 | 5 |
| 10 | 37 | 4 |
| 11 | 164 | 40 |
| 12 | 2734 | 313 |
| 13 | 5828 | 120 |
| 14 | 7793 | 2579 |
| 15 | 62431 | 27155 |
Experimental Cell Dose Measurement with HRRL
This experiment is done on 5/17/2010, at 10:00 am.
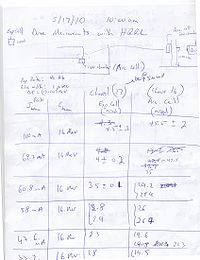
Dr. Khalid Chouffani wrote the note. Here is photocopy of his note:
page #1
page #2
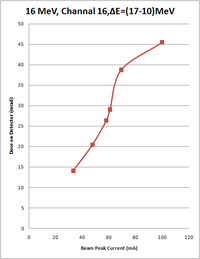
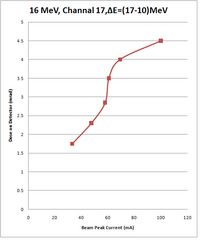
16 MeV Beam Energy
Experimental cell measurement with HRRL.
Conditions are:
Rap rate: 40 Hz
Pulse width: 1
E=(10-17) MeV
| Peak current of beam (mA) | Energy of beam (MeV) | Measurement on Channel 17, Experimental Cell (mrad) | Measurement on Channel 16, Accelerator cell (mrad) |
| 100 | 16 | 4.5 0.2 | 45.5 2 |
| 69.2 | 16 | 4 0.2 | 35, 42.5 |
| 60.8 | 16 | 3.5 0.1 | 29.2, 28.9 |
| 58.0 | 16 | 2.8, 2.9 | 26, 26.7 |
| 47.6 | 16 | 2.3 | 19.6, 21.3 |
| 33.2 | 16 | 1.8, 1.7 | 19.5, 19.0, 13.7 |
Beam bear through 1/4 inches diameter collimator with 4 inches lead.
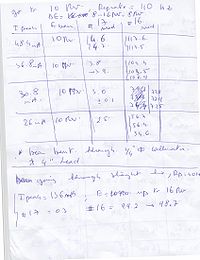
16 MeV Beam Energy
Conditions are:
Rap rate: 40 Hz
| Peak current of beam (mA) | Energy of beam (MeV) | Measurement on Channel 17, Experimental Cell (mrad) | Measurement on Channel 16, Accelerator cell (mrad) |
| 136 | 16 | 0.3 | 99.2, 98.7 |
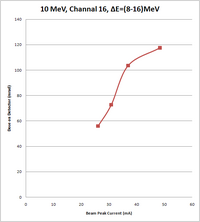
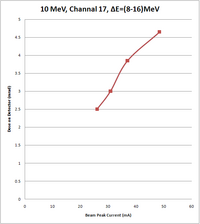
10 MeV Beam Energy
Conditions are:
Rap rate: 110 Hz
E=(8-16) MeV
| Peak current of beam (mA) | Energy of beam (MeV) | Measurement on Channel 17, Experimental Cell (mrad) | Measurement on Channel 16, Accelerator cell (mrad) |
| 48.4 | 10 | 4.6, 4.7 | 117.6, 117.5 |
| 36.8 | 10 | 3.8, 3.9 | 104.4, 103.5, 102.9 |
| 30.8 | 10 | 3.1 0.1 | 72.8, 72.9, 72.5 |
| 26 | 10 | 2.5 | 56.7, 56.4, 54.6 |
Channel 17 Dose Estimation in New Position
Channel 17 is a dose measuring detector on in the HRRL experimental cell.
1.Calculating number of particles per second
We have electron beam of:
Frequency: f (HZ)
Peak current: I (mAmp)
Pulse width:<math> ∆t= 1 ns=1*10^(-9)<math> seconds
So, how many electrons we have in each second?
By Q=It, we have
N*e=f*I*∆t
Where Ne is the total electron numbers hits target per second, e is electron charge and f, I and ∆t are given above. So
N= f*I*∆t/e=1000*0.01*5*10-8/(1.6*10-19)=3.12075*1012
So, we have around 3.12075*1012 electrons hit radiator per second.
Back to Positrons