PhD Proposal Tamar

Tamar PhD Proposal

Introduction

Media:HommezPhDThesis.ps

Electron scattering has been used for more than 40 years to measure the structure of a nucleon, a neutron or proton. The early experiments at SLAC discovered that a nucleon was composed of constituents called quarks. The constituent quark model views a baryon as a combination of three quarks and mesons as a quark-antiquark bound state. According to the quark model, the two of the three quarks in a proton are labeled as having a flavor "up" and the remaining quark a flavor "down". The two quarks have fractional charge [math]+\frac{2}{3}[/math] and spin [math]\frac{1}{2}[/math] oriented parallel to the direction of the proton spin and one quark with flavor type down, charge [math]-\frac{1}{2}[/math] and spin [math]-\frac{1}{2}[/math] antiparallel to the nucleon spin. In the quark model each quark carries one third of the nucleon mass.

While elastic scattering measures the ground state properties of a nucleon, inelastic scattering experiments are used to probe a nucleons excited states. The experiments at the SLAC used high energy electrons scattered by nucleons. The mediator between the target nucleon and coulomb scattering of an electron is the virtual photon. The four-momentum square of the virtual photon serves as a measure of the resolution of the scattering and may be formulated as:

[math]d = \frac{\hbar c}{Q} = \frac{0.2 \;\mbox {GeV} \cdot \mbox{ fm}}{Q}[/math]

The electron scattering data taken during the SLAC experiments revealed a scaling behavior, which was later defined as Bjorken scaling. The inelastic cross section was anticipated to fall sharply with Q^2 like the elastic cross section. The limited Q^2 dependence observed suggested that the nucleons constituents are pointlike. Independently, Richard Feynman introduced the quark parton model where the nucleons, a proton or neutron, are constructed by the three point like constituents, which were called partons. Shortly it was discovered that partons and quarks are the same particles. In the QPM the mass of the quark is much smaller than in the naive quark model. In the parton model the inelastic electron nucleon interaction via the virtual photon is understood as an incoherent elastic scattering processes between the electron and the constituents of the target nucleon. "In other words, one assumes that a single interaction does not happen with the nucleon as a whole, but with exactly one of its constituents."<ref> G. Dissertori, I.K. Knowles, M. Schmelling, Quantum Chromodynamics: High energy experiments and theory, International Series of Monographs on Physics No. 115, ISBN 0198505728, Oxford University Press, Feb. 2003</ref> In addition, two kind of quarks were introduced "sea" and "valence" quarks. The nature of the particle is defined by the valence quarks. The valence quarks in the proton are the up, up and down quarks. On the other hand, the so called sea quarks, virtual quarks and antiquarks, are constantly created from the vacuum.

A new theory of the quantum chromodynamics(QCD) proposed that in addition to the sea and valence quarks, there are neutral particles, gluons, that bind quarks together. Gluons are able to interact with each other and create virtual quark antiquarks pairs. In 1979 in three jet events at PETRA evidence of gluons was discovered. <ref>http://en.wikipedia.org/wiki/Three_jet_event</ref>

Baryon resonances

The understanding of the spin structure in the nucleon remains a major challenge for hadron physics. The parton model predicted that quarks carry about 60 % of the total nucleon spin. Experiments performed at CERN by EMC found out that only 12 % of the nucleon spin is carried by the quarks. Other experiments at CERN(SMC) and SLAC(E142 && E143) did not agree with the naive quark parton model. "This reduction is often attributed to the effect of a negatively polarized quark sea at low momentum fraction x, which is typically not included in quark models." The complete picture of the nucleon spin can be obtained by taking into account the spin contributions from the gluons, the sea quarks and in addition the quarks orbital momentum. So the spin of the nucleon can be written as the sum of the following terms<ref>B. Hommez, Ph.D Thesis, University of Gent (2003).</ref>:

[math]\frac{1}{2} = \frac{1}{2} \Delta \Sigma + \Delta G +L_z[/math]

where [math]\Delta \Sigma[/math] is the spin contribution from the quarks, [math]\Delta G[/math] - from the gluons and [math]L_z[/math] - the orbital angular momentum contribution from the partons(quarks).

Physics Motivation

In inclusive deep inelastic scattering only the the electron is detected in the final state and in the case of semi inclusive deep inelatic scattering the hadron is detected in coincidence with the scattered electron. Both physics processes can be characterized by the differential cross section. The cross section is equivalent to the detection rate. The differential cross section for the inclusive deep inelastic scattering can be written in terms of lepton and hadronic tensor<ref>R. G. Roberts, The structure of the proton, Cambridge Monographs on Mathematical Physics, ISBN 0521351596, Cambridge University Press, 1990.</ref> :

[math]\frac{d^2\sigma}{dxdQ^2} ~ L_{\mu \nu} W^{\mu \nu} [/math]

where the leptonic tensor [math]L_{\mu \nu}[/math] describes the coupling between the scattering lepton and the virtual photon, and the hadronic tensor [math]W^{\mu \nu}[/math] - the absorption of the virtual photon by the target nucleon. The hadronic tensor contains the information about the nucleon structure. It can be written in terms of structure functions using the symmetry arguments and conservation laws. However, the iformation about the spin distribution inside the nucleon is contained in the asymmetric part of the hadronic tensor. Which can be obtained by taking the difference of the cross sections with opposite spin states of the initial electrons beam. At JLAB the EG1 experiments is the double polarized experiment, because the target and the electron beam both were longitudinally polarized and only the spin of the electron was flipped.

The double spin asymmetry can be defined as the ratio of the difference between the cross sections when the spin of the initial electron beam is antiparallel and parallel to the target nucleon spin by the sum of this two quantities

[math]A_1 = \frac{\sigma_{1/2} - \sigma_{3/2}}{\sigma_{1/2} + \sigma_{3/2}}[/math]

where the cross section difference for polarized case is given by

[math]\frac{d^2 \sigma_{1/2} - d^2 \sigma_{3/2}}{dxdQ^2} = \frac{8 \pi \alpha^2}{Q^4} \frac{y}{E} [(E+E^' cos \theta)g_1(x,Q^2) - \frac{Q^2}{\nu}g_2(x,Q^2)][/math]

where E and [math]E^'[/math] are the initial and final energy of the electron, [math]\theta[/math] - the electron scattering angle, [math]Q^2[/math] - the four momentum transferred square, x and y - bjorken scaling variables, and [math]g_1[/math] and [math]g_2[/math] polarized structure functions, which contain information on the spin structure of the nucleon.
Measurement of the double spin asymmetry and the ratio of the polarized valence down quark distribution function to the unpolarized can be used to see the difference between the numerous descriptions of the nucleon structure. pQCD and a hyperfine perturbed constituent quark model predict the scaling variable [math]x_b[/math] = 1 corresponds to [math]A_n[/math]~1. On the other hand, the well-studied SU(6) constituent quark model for [math]x_b[/math]=1 states that [math]A_p=5/9[/math] and [math]A_n=0[/math]. Semi inclusive double spin asymmetry measurements using the CLAS Detector in combination with polarized proton and deuteron targets can considerably increase our knowledge on the nucleon structure.
From the Deep Inelastic Scattering a lot was learned about the quark gluon structure. The inclusive deep inelastic lepton-nucleon scattering experiments were used to measure the spin structure of the nucleon(the fraction of the spin of the nucleon which is carried by the quarks). Total nucleon spin is the sum of the nucleon spin due to quark spins, the quark orbital momentum and the total angular momentum of the gluons. IDIS provides information about the total quark spin contribution to the nucleon. Also the other issue is the inputs from the unmeasured low [math]x_B[/math] region and breaking SU(3) symmetry. From IDIS limited information can be obtained for the polarization of the sum of quarks and antiquarks. The reason is that the scattering cross section is proportional to the the square of the charge of the nucleon quark. need to understand more
On the other hand, semi inclusive deep inelastic scattering experiments, where the hadrons in the final state are detected in coincidence with the scattered lepton, are sensitive to the quark flavors. So it allows to separate different flavor quarks(quarks from antiquarks). "The technique of detecting hadrons in the final state to isolate contributions to the nucleon spin by specific quark and antiquark flavors is called flavor tagging.[ref.HERMES 1 paper]". The polarized quark distribution functions can be extracted from the SIDIS measurements using quark flavor tagging method excluding the assumptions used in inclusive DIS measurements. In SIDIS the double spin asymmetry can be expressed in terms of the cross sections of the produced hadrons during the experiment in the final state:

[math]A_1^h = \frac{\sigma_{1/2}^h - \sigma_{3/2}^h}{\sigma_{1/2}^h + \sigma_{3/2}^h}[/math]

where [math]\sigma_{1/2}^h[/math] ([math]\sigma_{3/2}^h[/math]) represents the semi inclusive cross section of hadrons type h which were produced in the final state when the spin of the initial electron beam is antiparallel(parallel) to the target nucleon spin.

good stuff

In the previous chapter it was mentioned that the measured structure function in the inclusive deep inelastic scattering experiments contains the contribution from the all different flavor quarks to the total nucleon momentum and spin, without distinguishing the input from the individual quark flavors. The semi inclusive deep inelastic scattering experiments give us opportunity to obtain the struck quark flavor, by detecting the hadron in the final state in coincidence with an electron.

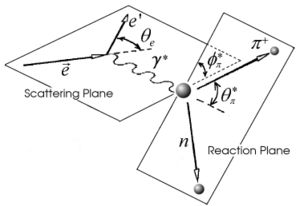
The kinematics of single pion electroproduction in SIDIS can be described by five variables: the virtual photon negative four-momentum transfered squared [math]Q^2[/math], W invariant mass of the photon-nucleon system, [math]{\theta_{\pi}}^*[/math] the polar and [math]{\varphi_{\pi}}^*[/math] the azimuthal angle of the outgoing pion in center of mass frame and [math]{\varphi}_e[/math] the scattered electron azimuthal angle. The incoming electron with four momentum [math]k = (E, \vec{k})[/math] is scattered of the target with four momentum [math](M, \vec{0})[/math], where M represents the rest mass of the target nucleon. The four momentums of the detected scattered electron and hadron are respectively [math]k^' = (E^', \vec{k^'})[/math] and [math]p_h = (E_h, \vec{p_h})[/math]. The semi inclusive deep inelastic scattering is shown below on Figure. 1. The four momentum of the exchanged virtual photon through which the SIDIS occurs is the four momentum loss of the initial electron

[math]q = k - k^'[/math]

The negative square of the four momenta can be written as [math]Q^2 = - {q^2} ^{lab} = 4EE^'\sin^2 \frac{\theta}{2}[/math], where [math]Q^2[/math] is greater then zero always. The energy transferred from the scattering electron to the target nucleon, which is also the enrgy of the virtual photon is given by

[math]\nu = \frac {P \cdot q}{M} =^{lab} E - E^'[/math]

The Bjorken scaling variables x and y are defined as

[math]x = \frac {Q^2}{2 P q} = \frac {Q^2}{2M \nu}[/math] and [math]y = \frac{P \cdot q}{P \cdot k} =^{lab} \frac{\nu}{E}[/math]

The energy fraction of the virtual photon transferred to a hadron, which is detected in the final state in coincidence with the scattered electron is following

[math]z = \frac{P\cdot p_h}{P\cdot q} =^{lab} \frac{E_h}{\nu}[/math]

and the last kinematical variable is the invariant mass of the scattering process which is available to produce the final hadronic state

[math]W^2 = (q + P_h)^2 = M^2 + 2 M \nu -Q^2[/math]

Table 1. Kinematic variables in deep inelastic scattering

Kinematic variable	Description
[math]k = (E, \vec{k})[/math], [math]k = (E^', k^')[/math]	4 - momenta of the initial and final state leptons
[math]\theta[/math], [math]\phi[/math]	Polar and azimuthal angle of the scattered lepton
[math]P^{lab} = (M, \vec{0})[/math]	4 - momentum of the initial target nucleon
[math]q = k - k^'[/math]	4 - momentum of the virtual photon
[math]Q^2 = - {q^2} ^{lab} = 4EE^'\sin^2 \frac{\theta}{2}[/math]	Negative squared 4 - momentum transfer
[math]\nu = \frac {P q}{M} =^{lab} E - E^'[/math]	Energy of the virtual photon
[math]x = \frac {Q^2}{2 P q} = \frac {Q^2}{2M \nu}[/math]	Bjorken scaling variable
[math]y = \frac{Pq}{Pk} =^{lab} \frac{\nu}{E}[/math]	Fractional energy of the virtual photon
[math]W^2 = (P + q)^2 = M^2 + 2M\nu - Q^2[/math]	Squared invariant mass of the photon-nucleon system
[math]p_h = (E_h, \vec{p_h})[/math]	4 - momentum of a hadron in the final state
[math]z = \frac{P\cdot p_h}{P\cdot q} =^{lab} \frac{E_h}{\nu}[/math]	Fractional energy of the observed final state hadron

i need to put definition

[math] \frac{d^2 \sigma}{dQ^2dW^2} = \frac{2 \pi \alpha^2 M}{(s-M^2)^2Q^2} [2W_1 (W^2,Q^2) + W_2(W^2,Q^2)(\frac{(s-M^2)(s-W^2-Q^2)}{M^2Q^2}-1)][/math]

where

The cross section in the target rest frame in terms of the initial and final energies of electron and electron scattering angle [math]\theta[/math]:

[math]\frac{d^2\sigma}{d\Omega d E^'} = \frac{\alpha^2 M}{8E^2E_p sin^4\frac{\theta}{2}}[2W_1sin^2\frac{\theta}{2} + W_2 \frac{4E^2_p}{M^2}cos^2\frac{\theta}{2}][/math]

where

[math]W_1[/math] and [math]W_2[/math] are so called structure functions, [math]E_p[/math] and E the energy of the initial proton and electron. [math]\theta[/math] - the direction of the scattered electron. M - mass of the target, in our case proton.

As it was mentioned above in the DIS an interaction doesnt happen with the hadron as a whole, but with exactly one of its constituents. Each quark(constituent) carries the fraction [math]x_i[/math] four-momentum of the nucleon with probability density [math]f_i(x_i). f_i(x_i)[/math] is the probability finding the ith quark with fraction [math]x_i[/math] of the proton(neutron) four-momentum. Assuming all this the structure functions can be written as sum of the elastic structure fractions weighted by the [math]f_i(x)[/math]. Taking in consideration that the mass of the ith quark is also the fraction [math]x_i[/math] of the nucleon mass [math]M_i = x_i M_h[/math]:

[math]W_1(Q^2, \nu ) =\Sigma_i \int_0^1 dx_i f_i(x_i) e_i^2 \frac{Q^2}{4x_i^2 M_h^2} \delta (\nu - \frac{Q^2}{2M_hx_i}) = \Sigma_i e_i^2 f_i(x_B)\frac{1}{2M_h}[/math]

and

[math]W_2(Q^2, \nu ) =\Sigma_i \int_0^1 dx_i f_i(x_i) e_i^2 \delta (\nu - \frac{Q^2}{2M_hx_i}) = \Sigma_i e_i^2 f_i(x_B)\frac{x_B}{\nu} [/math]

The DIS between the unpolarized electron and nucleon can be described in terms of two so called structure functions [math]F_1(x)[/math] and [math]F_2(x)[/math]:

[math]F_1(x) = M_h W_1 = \frac{1}{2}\Sigma_q e_q^2(q^+(x) + q^-(x)) = \frac{1}{2}\Sigma_q e_q^2q(x)[/math]

[math]F_2(x) = \nu W_2 =\frac{1}{2}\Sigma_q x e_q^2(q^+(x) + q^-(x)) = \frac{1}{2}\Sigma_q x e_q^2 q(x)[/math]

The relation between the structure functions [math]F_1(x)[/math] and [math]F_2(x)[/math] can be obtained from the following equation:

[math]F_2(x) \frac{1+\gamma^2}{1+R} = 2 x F_1(x)[/math]

where [math]R(x,Q^2)[/math] is the ratio of longitudinal to transverse deep inelastic scattering cross sections and [math]\gamma = \sqrt{\frac{Q^2}{\nu^2}}[/math]. In the naive quark parton model the longitudinal transverse interference is neglected.In the Bjorken limit it can be reduced to the Callan-Gross relation:

[math]F_2(x) = 2 x F_1(x)[/math]

"The structure function F_1 measures the parton density as function of x while [math]F_2[/math] describes the momentum density, both weighted with the coupling strength to the photon probe."

In the proton the distributions of up and down quarks are defined as u(x) and d(x), the same for neutron. The are two types of quarks: valence and sea quarks [math]u(x) = u_v(x) + u_s(x)[/math], assuming that [math]u_s(x)=\bar{u}(x)[/math]. The constituent quark model (QPM too) states that the proton(neutron) for example contains two up(down) and one down(up) quarks. So in the proton, summing over all the constituents should give us following:

[math]\int_0^1 dx u_v(x) = 2[/math]

and

[math]\int_0^1 dx d_v(x) = 1[/math]

The electromagnetic structure function for proton and neutron can be expressed in terms of quark distribution functions:

[math]F_2^{ep} = \frac{4}{9}[xu(x) + x\bar{u}(x) + xc(x) + x\bar{c}(x)] + \frac{1}{9}[xd(x) + x\bar{d}(x) + xs(x) + x\bar{s}(x)][/math]

[math]F_2^{en}[/math] can be obtained from [math]F_2^{ep}[/math] by replacing u->d and vice versa.

From the last two equations the structure functions for proton and neutron can be expressed in terms of valence quark distribution functions:

[math]F_2^{ep} = x [ \frac{4}{9} u_v(x) + \frac{1}{9} d_v(x) ][/math]

and

[math]F_2^{ep} = x [ \frac{4}{9} d_v(x) + \frac{1}{9} u_v(x) ][/math]

For most of the fixed-target experiments, like eg1b, the spin asymmetry is given by the ratio of the polarized structure function to the unpolarized: [math]A(x, Q^2) = \frac{g_1(x)}{F_1(x)}[/math], where the polarized structure function [math]g_1(x)[/math] is similar of the unpolarized structure function. The polarized structure function represents the helicity difference quark number density. As it is known the spin asymmetry and unpolarized structure function [math]F_1[/math] are measurable quantities and through them one can determine [math]g_1(x)[/math]:

[math]g_1(x) = \frac{1}{2} \Sigma_q e_q^2 (q^+(x) - q^-(x)) = \frac{1}{2}\Sigma_q e_q^2 \Delta q(x)[/math]

where [math]q^{+(-)}(x)[/math] is the quark distribution function with spin oriented parallel(antiparallel) to the spin of nucleon.

The polarized cross sections, which are related to the polarized structure function, are not measured directly. However the asymmetry related to them can be easily determined from the measurements:

[math]A_1 = \frac{\sigma_{1/2} - \sigma_{3/2}}{\sigma_{1/2} + \sigma_{3/2}}[/math]

where [math]\sigma_{1/2}[/math] ([math]\sigma_{3/2}[/math]) is the photon absorption cross section ones whose spin is antiparallel(parallel) to the target polarization. The photon of spin 1 is absorbed by only quarks whose spin is in the opposite direction from the photon's spin. Therefore, the polarized structure function can be related to the difference of these cross sections. However, the unpolarized structure function is the some of those two cross sections. The structure functions described above is based on quark parton model, where the contribution from the sea quarks is minimized. The double spin asymmetry can be written in terms of valence quark distribution functions for proton and neutron targets in this kinematic range:

[math]A_{1, p}^{I} = \frac {4\Delta u_v (x) + \Delta d_v (x)} {4 u_v (x) + d_v (x)} [/math] (1)

[math]A_{1, n}^{I} = \frac {\Delta u_v (x) + 4\Delta d_v (x)} {u_v (x) + 4d_v (x)} [/math] (2)

In inclusive DIS the asymmetry [math]A_{||}[/math] of cross sections, which is related to the beam and target polarization, only two measurable and controlled quantities, can be written in the following way:

[math]A_{meas} = P_B P_T f_D A_{||}[/math]

where [math]P_B[/math] and [math]P_T[/math] are the beam and target polarization respectively and [math]f_D[/math] - target dilution factor, the cross section factor caused by polarizable nucleons in the target.

In inclusive DIS the asymmetry of the photon absorption in the nucleon can be expressed in terms of the asymmetry [math]A_{||}[/math] of cross sections:

[math]A_{||} = D(1 + \eta \gamma )A_1[/math]

where [math]\eta = \frac{\epsilon \gamma y}{[1- (1-y) \epsilon ]}[/math] is a kinematic factor. The degree of polarization transfer from the electron to the virtual photon, so called depolarization factor D is given below:

[math]D = \frac{1- (1-y) \epsilon}{1 + \epsilon R}[/math]

where [math]\epsilon[/math] is the polarization parameter of the virtual photon:

[math]\epsilon = [1 + \frac{2 \vec{q}^2}{Q^2} tan^2 \frac{\theta}{2}]^{-1} = \frac{1 - y -\frac{1}{4} \gamma^2 y^2}{1-y+\frac{1}{4}y^2(\gamma^2+2)}[/math]

In inclusive DIS the polarization of the individual quarks(antiquarks) can be extrapolated from the fits to the data, relying on assumptions such as the Bjorken sum rule and SU(3) symmetry for the sea quark.

There is an alternative approach getting the information about the contributions from the individual quarks(antiquarks) using semi-inclusive Deep Inelastic Scattering instead of inclusive DIS, where in the final state in coincidence with the scattered lepton(in our case electron) hadron is detected too. In SIDIS after lepton scattering off the target emits an energetic virtual photon, which interacts with the quarks inside the nucleon. The energy and momentum transfer from the virtual photon to the quarks is so large that the struck quark is expelled from the nucleon forming the jet of hadrons. Hadrons created from the fragmentation of the expelled quark can be used as an one more method to tag its flavor. "This exploitation of hadrons in SIDIS measurements requires knowledge of the probabilities of the various types h of hadrons emerging from a struck quark of a given flavor q. These probabilities are embodied in the fragmentation function [math]D_q^h(z,Q^2)[/math], where [math]z=E_h/ \nu[/math] and [math]\nu[/math] and [math]E_h[/math] are the energies in the target rest frame of the absorbed virtual photon(th struck quark) and the detected hadron."[ref: flavor decomposition of the sea quark helicity dist. in the nucleon from SIDIS]. The correlation between the flavor of the probed quark and the detected hadron in the final state can be obtained from the fragmentation function, which is the probability that a quark of flavor q will fragment into a h type hadron. For instance, the detection of a [math]\pi^-[/math] meson in the final state, which is the bound state of [math]\bar{u}[/math](up anti) and d(down) quarks, indicates that either a [math]\bar{u}[/math](up antiquark) or a d(down) quark was probed in the nucleon. In addition, it is know that at high values of [math]X_B[/math] the Bjorken Scaling variable the sea quarks(like [math]\bar{u}[/math](up antiquark)) do not have a major contribution in the nucleon.

The semi-inclusive pion electro-production asymmetries can be written in terms of the cross sections of produced hadrons in the final state([math]\pi^-[/math] and [math]\pi^+[/math]):

[math]A[/math]^{[math]\pi^+ - \pi^-[/math]} =[math]\frac {\sigma^{\pi^+ - \pi^-}_{1/2} - \sigma^{\pi^+ - \pi^-}_{3/2}} {\sigma^{\pi^+ - \pi^-}_{1/2} + \sigma^{\pi^+ - \pi^-}_{3/2}} [/math]

Using Fragmentation function

The semi-inclusive cross sections can be expressed in terms of the quark distribution functions and fragmentation functions:

[math]\frac{d^3 \sigma^h_{1/2(3/2)}}{dxdQ^2 dz}\approx \Sigma_q e_q^2 q^{+(-)}(x,Q^2)D_q^h(z,Q^2)[/math]

Related measured asymmetry as we have for inclusive DIS [math]A_1[/math] is introduced for semi-inclusive asymmetry too, which is written in terms of fragmentation functions and quark helicity densities:

[math]A_1^h(x,Q^2,z) = \frac{\Sigma_q \Delta q(x,Q^2) D_q^h(z,Q^2)}{\Sigma_{q^'} q^'(x,Q^2) D_{q^'}^h(z,Q^2)} \frac{(1+R(x))}{(1+\gamma^2)}[/math]

In the last equation factoring out the ratio of polarized to unpolarized quark distribution functions and introducing new term, so called purity [math]P_q^h(x,Q^2,z)[/math], which is the probability that in the case when the beam and target are unpolarized after the scattering the created hadron type of h is detected in the final state is the result of probing a quark q in the nucleon. "The purities are extracted from the Monte Carlo simulation". So the above equation can be rewritten in the following manner:

[math]A_1^h(x,Q^2,z) = \Sigma_q P_q^h(x,Q^2,z)\frac{\Delta q(x,Q^2)}{q(x,Q^2)} \frac{(1+R(x))}{(1+\gamma^2)}[/math]

where purities are defined following way:

[math]P^h_q(x,Q^2,z) = \frac{e^2_q q(x, Q^2)\int_{0.2}^{0.8}D^h_q(z,Q^2)dz}{\Sigma_{q^'} e^2_{q^'} q^'(x, Q^2)\int_{0.2}^{0.8}D^h_{q^'}(z,Q^2)dz}[/math]

The double-spin asymmetry [math]A_1^h[/math] can be written in a matrix form:

[math]\vec{A}(x) = P(x) \cdot \vec{Q}(x)[/math]

where [math]\vec{A}(x)[/math] represents the measured asymmetries for different targets and the final states of the detected hadron: [math]\vec{A}(x) = (A_{1p},{A_{1p}}^{\pi^+},{A_{1p}}^{\pi^-}, A_{1d}, {A_{1d}}^{\pi^+}, {A_{1d}}^{\pi^-})[/math] and the polarization information for different flavors of quarks and antiquarks is in [math]\vec{Q}(x)[/math] vector: [math]\vec{Q}(x) = (\frac{\Delta u}{u},\frac{\Delta d}{d}, \frac{\Delta s}{s}, \frac{\Delta u^-}{u^-}, \frac{\Delta d^-}{d^-}, \frac{\Delta s^-}{s^-})[/math]. When the Bjorken scaling variable [math]x_B\gt 0.3[/math], region where the sea quark contribution is zero.

Independent from fragmentation function

• Extracting [math]\frac{\Delta d(u)}{d(u)}[/math]

In the semi inclusive deep inelastic scattering [math]\pi^+[/math] and [math]\pi^-[/math] production cross section can be written in the following way:

[math]\sigma = \frac{x(P+l)^2}{4 \pi \alpha^2} (\frac{2y^2}{1+(1-y)^2})\frac{d^3\sigma}{dxdydz}[/math]

and

[math]\Delta \sigma = \frac{x(P+l)^2}{4 \pi \alpha^2}(\frac{y}{2-y})[\frac{d^3\sigma_{+-}}{dxdydz} - \frac{d^3\sigma_{++}}{dxdydz}][/math]

P and l are the four momenta of the target and electron. \sigma_{nm} refer to a nucleon of n helicity and a scattering lepton(electron) of helicity m. Rest of the variables are described in Table.1.

The asymmetries from semi inclusive pion electroproduction for proton and deuteron targets can be written in terms of the difference of the yield from oppositely charged pions which is a measurable quantity:

[math]A_{1,p}^{\pi^+ \pm \pi^-} = \frac{\Delta \sigma_p^{\pi^+ \pm \pi^-}}{\sigma_p^{\pi^+ \pm \pi^-}}[/math]

[math]A_{1,2H}^{\pi^+ \pm \pi^-} = \frac{\Delta \sigma_{2H}^{\pi^+ \pm \pi^-}}{\sigma_{2H}^{\pi^+ \pm \pi^-}}[/math]

"Assuming independent fragmentation and using isospin and charge conjugation invariance for the fragmentation functions, i.e."

[math]D_u^{\pi^+ \pm \pi^-} = D_u^{\pi^+} \pm D_u^{\pi^-} = D_d^{\pi^+ \pm \pi^-}[/math]

Eliminating strange quark contributions the polarized and unpolarized cross sections for pion electroproduction can be expressed in terms of valence quark distribution functions:

[math]\Delta \sigma_p^{\pi^+ \pm \pi^-} = \frac{1}{9}[4(\Delta u + \Delta \bar{u}) \pm (\Delta d + \Delta \bar{d})]D_u^{\pi^+ \pm \pi^-}[/math]

[math]\Delta \sigma_n^{\pi^+ \pm \pi^-} = \frac{1}{9}[4(\Delta d + \Delta d^-) \pm (\Delta u + \Delta u^-)]D_u^{\pi^+ \pm \pi^-}[/math]

[math]\Delta \sigma_{2H}^{\pi^+ \pm \pi^-} = \frac{5}{9}[(\Delta u + \Delta \bar{u}) \pm (\Delta d + \Delta \bar{d})]D_u^{\pi^+ \pm \pi^-}[/math]

and unpolarized:

[math]\sigma_p^{\pi^+ \pm \pi^-} = \frac{1}{9}[4( u + \bar{u}) \pm ( d + \bar{d})]D_u^{\pi^+ \pm \pi^-}[/math]

[math]\sigma_n^{\pi^+ \pm \pi^-} = \frac{1}{9}[4(d + \bar{d}) \pm (u + \bar{u})]D_u^{\pi^+ \pm \pi^-}[/math]

[math]\sigma_{2H}^{\pi^+ \pm \pi^-} = \frac{5}{9}[( u + \bar{u}) \pm ( d + \bar{d})]D_u^{\pi^+ \pm \pi^-}[/math]

In the valence region where x_B>0.3, where sea quark contribution is minimized above asymmetries can be expressed in terms of polarized and unpolarized valence quark distributions:

[math]A_{1,p}^{\pi^+ \pm \pi^-} = \frac{4 \Delta u_v(x) \pm \Delta d_v(x)}{4u_v(x) \pm d_v(x)}[/math]

[math]A_{1,2H}^{\pi^+ \pm \pi^-} = \frac{\Delta u_v(x) + \Delta d_v(x)}{u_v(x) + d_v(x)}[/math]

After applying simple algebra the ratio of polarized to unpolarized valence up and down quark distributions are formulated as

[math]\frac{\Delta u_v}{u_v}(x,Q^2) = \frac{\Delta \sigma_p^{\pi^+ \pm \pi^-} + \Delta \sigma_{2H}^{\pi^+ \pm \pi^-}}{\sigma_p^{\pi^+ \pm \pi^-} + \sigma_{2H}^{\pi^+ \pm \pi^-}} (x,Q^2)[/math]

and

[math]\frac{\Delta d_v}{d_v}(x,Q^2) = \frac{\Delta \sigma_p^{\pi^+ \pm \pi^-} - 4\Delta \sigma_{2H}^{\pi^+ \pm \pi^-}}{\sigma_p^{\pi^+ \pm \pi^-} - 4\sigma_{2H}^{\pi^+ \pm \pi^-}} (x,Q^2)[/math]

The ratio of polarized to unpolarized valence quark distribution functions can be extracted using the last two equations.

• Fragmentation Function test

A complete test of independent fragmentation can be performed with polarized proton and neutron targets. An asymmetry we consider to be following [math]\Delta R_{np}^{\pi^+ + \pi^-}[/math]:

[math]\Delta R_{np}^{\pi^+ + \pi^-} = \frac{\Delta \sigma_p^{\pi^+ + \pi^-} - \Delta \sigma_{n}^{\pi^+ + \pi^-}}{\sigma_p^{\pi^+ + \pi^-} - \sigma_{n}^{\pi^+ + \pi^-}}=[/math]

[math]=\frac{(\Delta u +\Delta \bar{u}) - (\Delta d + \Delta \bar{d})}{(u+\bar{u}) - (d+\bar{d})}(x,Q^2)=[/math]

[math]= \frac{g_1^p - g_1^n}{F_1^p - F_1^n}(x,Q^2)[/math]

The last expression of the asymmetry [math]\Delta R_{np}^{\pi^+ + \pi^-}[/math] was obtained from because of that :) {need to change} :

[math]g_1^p - g_1^n = \frac{1}{6}[(\Delta u +\Delta \bar{u}) - (\Delta d + \Delta \bar{d})][/math]

and

[math]F_1^p - F_1^n = \frac{1}{6}[(u+\bar{u}) - (d+\bar{d})][/math]

"Independent fragmentation would hold if the measured asymmetry [math]\Delta R_{np}^{\pi^+ + \pi^-}[/math] followed the x and [math]Q^2[/math] behavior of the quantities [math]g_1[/math] and [math]F_1[/math] measured in deep inelastic scattering independent of z."

Media:Semi-inclusive_π_production_tests_for_independent_fragmentation_and_for_polarized_quark_densities.pdf

Quark distribution function q(x) is the probability(density) of finding a quark with fraction x of the proton(neutron) momentum.

Experimental Setup

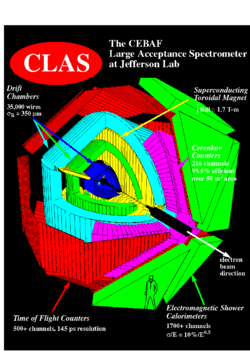
The CEBAF large acceptance spectrometer (CLAS) located in Jefferson Lab's Hall B was used to measure the final state particle resulting from the scattering of a polarized electron by a polarized nucleon. The CLAS used six superconducting coils produce a toroidal magnetic field along the beam direction. A set of three drift chambers is placed to determine the trajectories of particles which pass through the 6 gaps between the magnet coils. The first drift chamber, Region 1 (R1), is place at the entrance to the magnetic coil. A second chamber, Region 2 (R2), is placed in the center of the coils. The final chamber, Region 3 (R3), measures charged particle leaving the toroidal field. A total of 18 drift chambers are used to reconstruct the trajectory of charged particles passing through the magnetic field. After the drift chamber system, the CLAS detector is equiped with Cherenkov counter for separating electrons from pions and with scintillators for determination of the Time of Flight of a charged particle. At the end of the detector the particle identification and timing(resolution) is achieved using electromagnetic calorimeters. Five different targets were used during the experiment: [math]15ND_3[/math], [math]15NH_3[/math],C12, liquid He-4 and frozen N15. In order to remove background from the first two types of target the measurements were done with last three targets listed above.

Target

Target Materials

The EG1 experiment at Jefferson Lab used five different targets to measure polarized structure functions of the nucleon and perform background corrections. The main target materials for the experiment used frozen ammonia, [math]15NH_3[/math], for the polarized protons and deuterated ammonia, [math]15ND_3[/math] for the polarized deuterons. The target vessel, known as the target ladder, was designed and built by collaboration of the Italian Istituto di Fisica Nucleare, TJNAF, Oxford instruments and the University of Virginia. The solid targets(NH3 and ND3) were polarized using the method of Dynamic Nuclear Polarization <ref>Prok Thesis</ref>. Three other targets, C12, liquid He-4 and frozen N15 were used to remove the Nitrogen background from NH3 and ND3 target data.

there is a figure of merit which considers max polarization and radiation damage, Li-6 is a competitor

Ammonia targets were selected because of their ability to produce high polarization and they are less effected by beam radiation. On the other hand, the damage caused by this radiation can be repaired by annealing. The target is warmed up to liguid nitrogen temperature for annealing. In addition, the ammonia target has a high ratio of free nucleons (~3/18) approximately 16.5 % for [math]15NH_3[/math] and 26.6 % for [math]15ND_3[/math]. One disadvantage of choosing ammonia is the polarization background caused by 15N(spin - 1/2), or 14N(spin - 1), which was accounted for by taking data using a solid N-15 target.[SChen_FSU_thesis]

Magnet

A 5 T magnetic field is established using a produced pair of superconducting Helmholtz coils oriented such that the magnetic field is parallel to the beam direction. The field induces the hyperfine splittings needed to polarize the target material using ? Ghz RF waves. The uniformity of the field is varying less than [math]10^{-4}[/math] over a cylindrical volume of 20 mm in diameter and length. This configuration is necessary for DNP. The particles with scattering angles between 0-50 are detected in the CLAS as well as 75-105 due to the 8 cm gap between the Helmholtz coils. The target magnetic field does not interact with the electron beam, however it is effective in shielding the drift chambers from the low energy Moller electrons.The target field bents the scattered particles in the azimuthal direction and it falls rapidly with distance as ([math]~ 1/r^3[/math]). The effect of magnetic field at the drift chambers is negligible.[ref 2]

The CEBAF Large Acceptance spectrometer

• The Torus Magnet

The torus magnet for CLAS detector consists the six superconducting coils located around the beam line in a toroidal geometry, producing the magnetic field in the [math]\varphi[/math] direction. Each magnetic coil defines the sector of detector. So the CLAS detector has six sectors(spectrometer). The system of the magnet is defined in spherical coordinates where the z-axis are along the beam direction and the x and y axis along the horizontal and vertical plane normal to the beam line.
The maximum current for the CLAS magnet is 2860 A, in the forward direction the total magnetic field is 2.5 T-m and at a polar scattering angle with 90 degrees 0.6 T. The magnet itself is around 5 m in diameter and 5 m in length. The coils of the magnet are cooled by liquid helium circulating through cooling tubes to a superconducting temperature of 4.5 K.[[Yelena Alexsandrovna Pork, Measurement of The spin Structure Functions [math]g_1 (x, Q^2)[/math] of The Proton in The resonance Region.]] One can find out the charged particles momentum knowing the trajectory of a particle. In Eg1b experiment, the operated torus values were: 2250, -2250, 1500, -1500.

• Drift Chambers

In order to track the charged particles in the EG1b experiment a drift chamber system is used. A drift chamber is a particle tracking detector that measures the drift time of ionization electrons in a gas to calculate the spacial position of an ionizing particle.
The electric field in a drift chamber is produced by the anode(sense wire) and cathode(field wire) wires. The charge particle traveling trough the drift chamber ionizes the gas, producing the electrons that drift to the anodes. After [math]\delta t[/math] time(drift time) electrons are collected at the anode(sense wire) generating the pulse at t time. The distance from the traversing particle to the sense wire can be calculated using the drift time and velocity.
The drift chamber system in CLAS detector is divided into three regions, each consisting six separate chambers(six sectors). Region 1 (R1) chambers are placed closest to the target, where the magnetic filed is low. Region 2 (R2) chambers are in a high magnetic field region, they are located between the magnetic coils. Region 3 (R3) chambers are outside the torus coils and they are largest ones. The drift chambers contain three type of wires stretched between the endplates: sense, guard and field. The endplates are attached to the drift chamber so that the angle the form is equal to 60 degrees. Each drift chamber is subdivided into two separate superlayers. Each superlayer with six layers of drift cells, and each drift cell with one sense wire surrounded by six field wires forming a hexagonal shape([1]). Each superlayer is surrounded by guard wires at a positive potential to stimulate the electric field caused by the drift cells. The sense wire is operated at positive potential and the field wire at negative. In each superlayer the distance between the sense and field wire increases with the radial distance from the target. In R1 the average distance between the sense and field is 0.7 cm, in R2 1.15 cm and in R3 2.0 cm.
The gas used to fill the CLAS drift chamber is a 90 - 10 % mixture of the argon(Ar) and [math]CO_2[/math], where Ar has an ionization gain of [math]~ 10^4[/math]. Inside the drift chamber the constant pressure is provided by outflowing the gas. The chamber endplates are equipped with the circuit board with a single channel differential pre-amplifier for each sense wire.

• Cherenkov detector

The threshold CLAS Cherenkov detector is used to distinguish electrons from pions. The mixture gas used to fill the Cherenkov counter is perfluorobutane [math]C_4 F_{10}[/math] gas at atmospheric pressure. The advantage of Perfluorobutane [math]C_4 F_{10}[/math] gas is its high index of refraction n=1.00153, which results in a high photon yield and the following energy thresholds. The threshold for the Cerenkov radiation can be written as [math]v\gt c/n[/math], or for energies [math]E\gt \gamma \times m[/math], where v is the velocity of charged particle, n index of refraction for the medium, c speed of light and [math]\gamma = \frac{1}{\sqrt{1 - \frac{1}{n^2}}}[/math]. In our case [math]\gamma = 18.098[/math], accordingly one can calculate the energy threshold for different charged particles, for electrons it is 9 MeV and for pions 2.5 GeV.
The Cherenkov detector was designed to maximize the coverage in each of the sectors up to an angle [math]\theta=45[/math] degrees.The CLAS Cherenkov DetectorG. Adamsa, V. Burkertb
As a light collector were used the system of mirrors , the light collecting cones and photomultiplier tubes(PMTs). In the extreme regions of the angular acceptance of the spectrometer the number of detected photoelectrons is too low. To get acceptable efficiency of the detector in these regions photomultiplier tubes were placed. The calibration of the Cherenkov detector is in terms of the collected number of photoelectrons.

• Scintillators

The CEBAF Large Acceptance Spectrometer (CLAS) is equipped with 288 scintillator counters. The purpose of the scintillator is to determine the time of flight for the charged particles and to trigger it in coincidence with another detector system for the particle identification. The time of flight system is built so that time resolution at small polar angles [math]\sigma =120[/math]ps and at angles above 90 degrees [math]\sigma=250[/math]ps. This time resolution helps to discriminate pions and kaons up to 2 GeV/c.
The time of flight system is located between the Cherenkov detectors and electromagnetic calorimeters. The scintillator strips(BC_408) are located perpendicularly to the average particle trajectory with an angular polar coverage of 1.5 degrees. Each sector of The CLAS detector consists of 48 scintillator strips with a thickness of 5.08 cm. The length of the scintillators varies from 30 cm to 450 cm and the width is between 15 cm at small polar angles and 22 cm for the large angles.

• Calorimeter

The CLAS detectur contains 8 modules of electromagnetic calorimeter. A calorimeter is a device that measures the total energy deposited by a crossing particle. They are useful in detecting neutral particles and distinguishing between electrons and hadrons due to their different mechanism of depositing energy. The CLAS calorimeter has three main functions:
1) detection of electrons at energies above 0.5 GeV;
2) detection of photons with energies higher than 0.2 GeV;
3) detection of neutrons, with discrimination between photon and neutrons using time-of-flight technique.
6 calorimeter modules of the CLAS detector are placed in each sector in the forward region (polar angle of 10-45 degrees, forward angle calorimeter), while the other two modules are located at large angles in sectors 1 and 2(50-70 degrees, large angle calorimeter). The forward calorimeter has a lead/scintillator thickness ratio 0.2, with 40 cm of scintillators and 8 cm of lead per module. The lead-scintillator sandwich is shaped as a equlaterial triangle in order to match the hexagonal geometry of the CLAS detector. It is made of 39 layers of a 10 mm BC_412 scintillator and lead sheet of thickness of 2.2 mm. Each scintillator layer contains 36 strips parallel to one side of the triangle, with this configuration each orientation is rotated by 120 degrees from another one. This gives three views each containing 13 layers providing stereo information of the location of the energy deposition. To improve hadron identification, there was provided longitudinal sampling of the shower. Each set of 13 layers were subdivided into an inner 5 layers and outer 8 layers stack.

Experiment running conditions

Table of Beam energy, current, polarization, targets, polarizations, Torus setting, Trigger

Preliminary Results

The differential cross-section and electron beam asymmetries were measured using the CEBAF Large Acceptance spectrometer (CLAS) at Thomas Jefferson National Lab with a 5.7?? GeV continues electron beam of [math] 1.09209 \times 10^{33} \frac{[ \# of electrons]}{second \times cm^2}[/math] luminosity and polarized target(frozen ammonia) and compared to the E99-107 data.
The kinematics of single pion electroproduction can be described by five variables: the virtual photon negative four-momentum transfered squared [math]Q^2[/math], W invariant mass of the photon-nucleon system, [math]{\theta_{\pi}}^*[/math] the polar and [math]{\varphi_{\pi}}^*[/math] the azimuthal angle of the outgoing pion in center of mass frame and [math]{\varphi}_e[/math] the scattered electron azimuthal angle. The four-momentum transfered squared [math]Q^2 = - (k - k^') ^{2} = 4EE^'\sin^2 \frac{\theta_e}{2}[/math], where k(E) nd [math]k^'[/math]([math]E^'[/math]) are the initial and final four-momentum(energy) of the electron in the laboratory frame and [math]\theta_e[/math] - electron scattered angle. The invariant mass [math]W^2 = (P_{\gamma} + P_h)^2 = M_p^2 + 2 M_p \nu + -Q^2[/math], where [math]P_{\gamma}[/math] and [math]P_h[/math] are four-momenta of the virtual photon and target respectively, [math]M_p[/math] is proton mass and [math]\nu = \frac{P_h \cdot P_{\gamma}}{M_p} = E - E^'[/math] the virtual photon energy.

Kinematics of single [math]\pi^+[/math] electroproduction

The five-fold differential cross section can be written in the following way for a single pion electroproduction:

[math]\frac{\partial^5 \sigma}{\partial E_f \partial \Omega_e \partial {\Omega_{\pi}}^*} = \frac{1}{2 \pi} \Sigma \frac{1}{L_{int} A_{cc} \epsilon_{CC} \Delta W \Delta Q^2 \Delta cos {\theta_{\pi}}^* {\phi_{\pi}}^*} \frac{d(W, Q^2)}{d(E_f, cos \theta_e)}[/math]

where [math]\epsilon_{CC} [/math] represents the efficiency of the cherenkov detector, [math]L_{int}[/math] - the integrated luminosity, [math]A_{cc}[/math] is the acceptance factor and the Jacobian term can be expressed in terms of the initial and final energy of lepton:

[math]\frac{d(W, Q^2)}{d(E_f, cos \theta_e)} = \frac{2 M_p E_i E_f}{W}[/math]

Cuts

In the semi-inclusive asymmetry analysis scattered electrons are used. The contamination in the electron sample is removed using the cuts on the energy deposited in the electromagnetic calorimeter, the number of photoelectrons in the Cherenkov counter and fiducial cuts(there should be vertex cut too). the energy deposition in the calorimeter for electrons and pions is different. Pions are minimum ionizing charge particles and energy deposited into the calorimeter, independent of the particles momentum is constant. It is approximately ~ 0.08 GeV. On the other hand, electrons produce photoelectrons and create electromagnetic shower releasing the energy into the calorimeter which is proportional to their momentum. In order to remove contamination due to the energy deposition in the calorimeter the following cut was introduced: [math]EC_{total}\gt 0.2*p[/math]. The cut was also applied to the energy collected in the inner part of the calorimeter: [math]EC_{inner}\gt 0.06*p[/math] , because the ratio of the energy deposited in the total to the inner calorimeter depends on the thickness of the detector and is a constant.

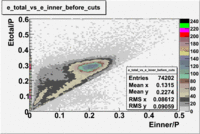
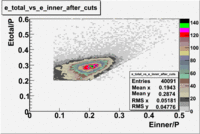
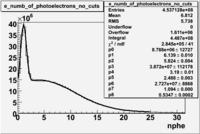
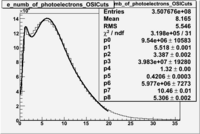
In addition to the cut on the energy deposited into the electromagnetic calorimeter, the misidentified electrons were excluded requiring a signal in the threshold CLAS Cherenkov detector, which is used to distinguish electrons from pions up to 2.5 GeV momentum of the particle. The energy threshold for electrons in the Cherenkov counter is 9 MeV and for pions 2.5 GeV. There are no many pions above 2.5 GeV momentum(should rewrite). A bad recollection of the cherenkov light that occurs for a particular kinematics is responsible for a faulty peak around ~1.5 on the number of photoelectons distribution shown below. To eliminate the faulty peak and high energy pions, which have enough energy to produce photons the geometrical cuts were applied on the data. The second histogram below shows that after cuts the peak around 1.5 disappears. (i need to discuss about nphe>2.5 cut)

No cuts	OSI Cuts
The number of photoelectrons without cuts	The number of photoelectrons with OSI cuts

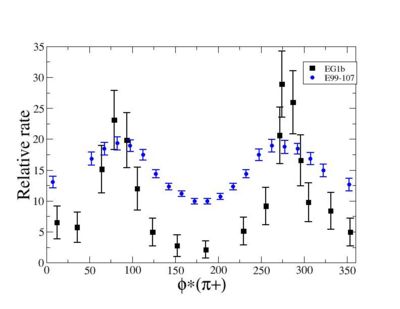
Because of wide range of kinematics, [math]{\varphi_{\pi}}^*[/math] was measured only for certain lepton scattering [math]\theta_e[/math]?? angle and W invariant mass. Applying above described cuts: EC_inner>0.06, EC_tot/p>0.2, nphe>2.5 and [math]0.9\lt M_x\lt 1.1[/math], for he following invariant mass [math]1.44\lt W\lt 1.46[/math] and [math]0.6\lt cos\theta_{pion}^{CM}\lt 0.8[/math] the [math]{\varphi_{\pi}}^*[/math] vs relative rate distribution is shown below on the graph and compared with E99-107 data.

[math]{\varphi_{\pi}}^*[/math] vs Relative rate for fixed [math]cos\theta_{pion}^{CM}=0.7[/math] and [math]W=1.45 GeV[/math]

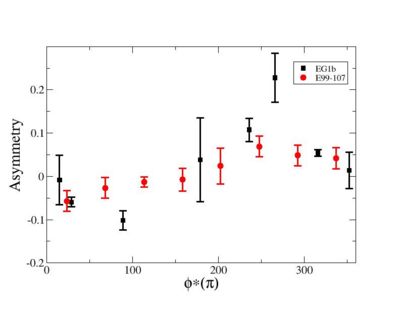
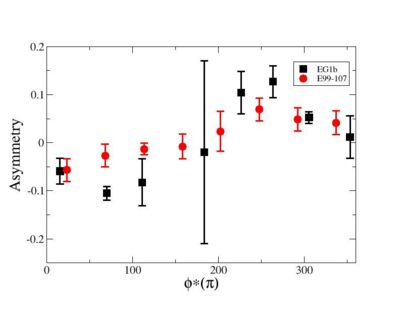
Electron Beam Asymmetry

[math]A = \frac{N^+ - N^-}{N(N^+ - N^-)}[/math]

[math]{\varphi_{\pi}}^*[/math] vs Electron beam helicity asymmetry for [math]W=1.40 GeV[/math] and [math]cos\theta_{pion}^{CM}=0.1[/math]. EG1b compared to E99-107 data [math]{\varphi_{\pi}}^*[/math] vs Electron beam helicity asymmetry for [math]W=1.40 GeV[/math] and [math]cos\theta_{pion}^{CM}=0.1[/math]. EG1b compared to E99-107 data

Notes

<references/>

[2]

Charge Conjugation Invariance Invariances, in particle physics, are relationships between different processes.

Charge conjugation is the replacement of each particle in a process by the corresponding antiparticle. Charge conjugation invariance states that the rate of a process is identical to the rate of a similar process with all particles replaced by their antiparticles. Charge conjugation invariance is true for strong and electromagnetic interactions, but not for weak interactions.