Difference between revisions of "Forest Relativity Notes"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
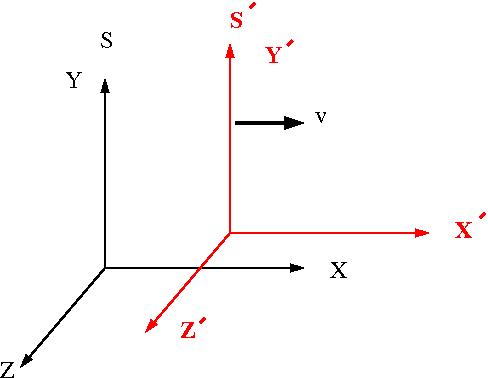
=Lorentz Transformations= | =Lorentz Transformations= | ||
| + | [[Image:ForestRelativityLorentzFrame.jpg]] | ||
:<math>x^{\mu^{\prime}} = \sum_{\nu=0}^3 \Lambda_{\nu}^{\mu} x^{\nu}</math> | :<math>x^{\mu^{\prime}} = \sum_{\nu=0}^3 \Lambda_{\nu}^{\mu} x^{\nu}</math> | ||