TF SPIM StoppingPower

Stopping Power

Bethe Equation

Classical Energy Loss

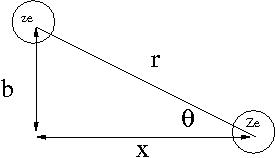
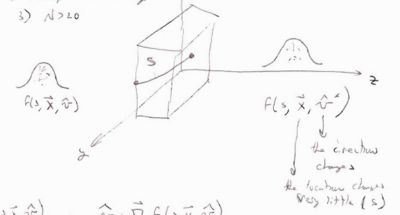
Consider the energy lost when a particle of charge ($ze$) traveling at speed $v$ is scattered by a target of charge ($Ze$). Assume only the coulomb force causes the particle to scatter from the target as shown below.

Notice

as $ze$ is scattered the horizontal component of the coulomb force ($F$) flips direction; ie net horizontal force for the scattering

$F_{vertical} = k \frac{zZe^2}{r^2} \sin(\theta) = k \frac{zZe^2}{r^2} \frac{b}{r}$

where

k =$\frac{1}{4 \pi \epsilon_0}$

r = distance between incident projectile and target atom

b= impact parameter of collision

Using the definition of Impulse one can determine the momentum change of $ze$ as

$\Delta p = \int F dt$

Let's assume that the energy lost by the incident particle $ze$ is absorbed by an electron in the target atom. This energy may be cast in terms of the incident particles momentum change as

$\frac{(\Delta p)^2}{2m_e}$

By calculating the change in momentum ($\Delta p$) of the incident particle we can infer that the energy lost by the incident particle is absorbed by one of the target material's atomic electrons.

$\Delta P = \int F dt = \int k \frac{zZe^2b}{r^3} dt$

using $dt = \frac{dx}{v} = \frac{d x}{\beta c}$ we have

$= k \frac{zZe^2b}{\beta c} \int_{-\infty}^{+\infty} \frac{ dx}{(x^2+b^2)^{3/2}}$

$=\frac{kzZe^2b}{\beta c b^2} \int_{-\infty}^{+\infty} \frac{ dx/b}{(1+\frac{x^2}{b^2})^{3/2}}$

$\int_{-\infty}^{+\infty} \frac{ dx/b}{(1+\frac{x}{b^2})^{3/2}}=2$

$\Delta p = \frac{2kzZe^2b}{\beta c b^2}$

casting this in terms of the classical atomic electron radius $r_e$

$r_e = \frac{k e^2}{m_e v^2} \sim \frac{k e^2}{m_e c^2}$ just equate $F = \frac{ke^2}{r_e^2} = m \frac{v^2}{r_e}$

Then

$\Delta p = \frac{2zZr_e m_e c}{\beta b}$

and

$\Delta E = \frac{(\Delta p)^2}{2m_e} = 2 \left ( \frac{r_e m_e}{\beta b}\right )^2 \frac {z^2 Z^2 c^2}{m_e}$ : $Z$ = 1 here because I shall assume the energy is lost to just the electron and the Atom is a spectator

Now let's calculate an expression representing the AVERAGE energy lost for an incident particle traversing a material of some thickness.

Let

$P(\Delta E)$ = Probability of an interaction taking place which results in an energy loss $\Delta E$

If we let

Z = Atomic Number = # electrons in target Atom = number of protons in an Atom

N = Avagadros number = $6.022 \times 10^{23} \frac{Atoms}{mol}$

A = Atomic mass = $\frac{g}{mole}$

$dP(\Delta E)$ = probability of hitting an atomic electron in the area of an annulus of radius ($b + db$) with an energy transfer between $\Delta E$ and $\Delta E + d(\Delta E)$

Then

$\frac{-dE }{dx}= \int_0^{\infty} dP(\Delta E) \Delta E$ = energy lost by the incident particle per distance traversed through the material

I am just adding up all the energy losses weighted by the probability of the energy loss to find the average (total) energy loss.

What is $dP(\Delta E)$

$dP(\Delta E)$ = probability of an energy transfer taking place = probability of an interaction = $\frac{N}{A} d \sigma$ [ Atoms $cm^2$/g]

$dP(\Delta E) = \frac{N}{A} d \sigma =\frac{N}{A} (2 \pi b db) Z$

In practice $\sigma$ is a measured cross-section which is a function of energy.

classically $\sigma = \pi b^2 ; d \sigma = 2\pi b db$ so let's use this as a first approximation

$\Rightarrow \frac{-dE}{dx} = \int_0^{\infty} \frac{N}{A} (2 \pi b db) Z \Delta E = \frac{2 \pi N Z}{A} \int_0^{\infty} \Delta E b db$

= $\frac{2 \pi N Z}{A} \int_0^{\infty} \left [ \frac{2 r_e^2 m_e c^2 z^2}{\beta^2 b^2}\right ] b db$

= $4 \pi N r_e^2 m_e c^2 \frac{z^2 Z}{A \beta^2} \int_0^{\infty} \frac{db}{b}$

=$\frac{\mathcal{K} }{A} \frac{z^2 Z}{\beta^2} \int_0^{\infty} \frac{db}{b}$

where $\frac{\mathcal{K}}{A} = \frac{4 \pi N r_e^2 m_e c^2}{A} = 0.307 \frac{MeV cm^2}{g}$ if A=1

The limits of the above integral should be more physical in order to reflect the limits of the physics interaction. Let $b_{min}$ and $b_{max}$ represent the minimum and maximum possible impact parameter where the physics is described, as shown above, by the coulomb force.

What is $b_{min}$?

if $b \rightarrow 0$ then $\frac{d E}{dx}$ diverges and the energy transfer $\rightarrow \infty : \Delta E \sim \frac{1}{b}$. Physically there is a maximum energy that may be transferred before the physics of the problem changes (ie: nuclear excitation, jet production, ...). The de Borglie wavelength of the atom is used to estimate a value for $b_{min}$ such that

$b_{min} \sim \frac{1}{2} \lambda_{de Broglie} = \frac{h}{2p} = \frac{h}{2 \gamma m_e \beta c}$

What is $b_{max}$?

As $b$ gets bigger the interaction is "softer" and longer. If the interaction time ($\tau_i$) is so long that it is equivalent to an electron orbit ($\tau_R$) then the atom looks more like it is neutrally charged. You move from an interaction in which the electron orbit is perturbed adiabatically such that there is no orbit change and the minimum amount of energy is transferred to no interaction taking place because the atom is neutral.

Let

$\tau_i = \frac{b_{max}}{v} (\sqrt{1-\beta^2})$ : fields at high velocities get Lorentz contracted

$\tau_R \equiv \frac{h}{I}$ : I $\equiv$ mean excitation energy of target material ( $E = h \nu = h/ \tau$)

Condition for $b_{max}$ :

$\tau_i = \tau_R$

$\Rightarrow b_{max} = \frac{h \gamma \beta c}{I}$

$-\frac{dE}{dx} = \frac{\mathcal{K} }{A} \frac{z^2 Z}{\beta^2} \int_0^{\infty} \frac{db}{b}$

$= \frac{\mathcal{K} }{A} \frac{z^2 Z}{\beta^2} \ln \frac{b_{max}}{b_{min}}$

$= \frac{\mathcal{K} }{A} \frac{z^2 Z}{\beta^2} \ln \frac{2 \gamma^2 m_e \beta^2 c^2}{I}$

Example 5: Find $\frac{dE}{dx}$ for a 10 MeV proton hitting a liquid hydrogen ($LH_2$) target

A = Z=z=1
$m_e c^2$ = 0.511 MeV
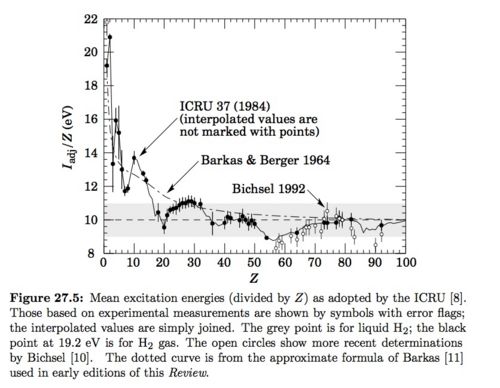
I = 21.8 eV : see gray data point for Liquid $H_2$ From Figure 27.5 on pg 6 of PDG below.

Just need to know $\gamma$ and $\beta$

"a 10 MeV proton" $\Rightarrow$ Kinetic Energy (K.E.) = 10 MeV = $(\gamma - 1) mc^2$

$\Rightarrow \gamma = \frac{K.E.}{mc^2} + 1 = \frac{10 MeV}{938 MeV} + 1 \sim 1 = \frac{1}{\sqrt{1-\beta^2}}$

Proton is not relativistic

$v^2 = \frac{2 K.E.}{m} = \frac{2 \cdot 10 MeV}{938 MeV/c^2} = 2 \times 10^{-2} c^2 \Rightarrow \beta^2 = \frac{v^2}{c^2} = 2\times 10^{-2}$

Plugging in the numbers:

$\frac{dE}{dx} = \left ( 0.307 \frac{MeV \cdot cm^2}{g}\right ) (1)^2 (1) \frac{1}{2 \times10^{-2}} \ln \left( \frac{2 (1) (0.511 MeV) (2 \times10^{-2})}{21.8 eV} \frac{10^6 eV}{MeV}\right)$

$= 105 \frac{MeV cm^2}{g}$

How much energy is lost after 0.3 cm?

Notice that the units for energy loss are normalized by the density of the material $\rho_{LH_2}$ = 0.07 $\frac{g}{cm^3}$

To get the actual energy lost I need to multiply by the density. So for any given atom the energy loss will depend on the state (solid, gas, liqid) of the atom as this effects the density of the material.

$\Delta E = (105 \frac{MeV cm^2}{g}) (0.07 \frac{g}{cm^3}) (0.3 cm)$ = 2.2 MeV

File:SPIM HydrogenStoppingPower.pdf Compare with Triumf Kinematics Handbook, 2nd edition, September 1987, L.G. Greeniaus

Bethe-Bloch Equation

While the classical equation above works in a limited kinematic regime, the Bethe-Bloch equation includes the corrections needed to cover most kinematic regimes for heavy particle energy loss.

$-\frac{dE}{dx} = \mathcal{K} z^2 \frac{Z}{A} \frac{1}{\beta^2} \left [ \frac{1}{2} \ln \left (\frac{2 m_e c^2 \beta^2 \gamma^2 }{I} \frac{ T_{max}}{I} \right) - \beta^2 - \frac{\delta}{2}\right ]$PDG reference Eq 27.1 pg 1

where

$T_{max} = \frac{2 m_e c^2 \beta^2 \gamma^2}{1+ \frac{2 \gamma m_e}{M} + \frac{m_e}{M}}$

= Max K.E. transferable to the Target of mass $M$ in a single collision.

$-\beta^2$

= correction for electron spin and very distant collisions which deforms the electron atomic orbits each process reducing dE/dx by $\frac{\beta}{2}$

$\frac{\delta}{2}$

= density correction term: in the classical derivation the material is treated as just a system of $N$ atoms uniformly distributed in space. These Atoms, however, give the material polarizability which can reduce the electric field (dielectric).

GEANT 4 implementation

The GEANT4 file (version 4.8.p01)

source/processes/electromagnetic/standard/src/G4BetheBlockModel.cc

is used to calculate hadron energy loss.

line 132 (line 257 in version 4.9.5) $\Rightarrow$

$-\frac{dE}{dx} = \log \left ( \frac{2 m_e c^2 \tau (\tau +2) E_{min}}{I^2}\right) - \left (1 - \frac{E_{min}}{E_{max}} \right ) \beta^2$

where

$\tau = \frac{K.E.}{M}$

line 143 (line 267 in version 4.9.5) $\Rightarrow$

$\frac{dE}{dx} -= \log ( \tau (\tau + 2) ) -cden$ = density corection = $\frac{\delta}{2}$

line 148 (line 270 in vers. 4.9.5) $\Rightarrow$

$\frac{dE}{dx} -= \frac{2c}{Z_{target}}$ = shell correction, corrects for the classical asumption that the atomic electron's velocity is initially zero; or the the incident particles velocity is far greater than the atomic electron's velocity.

line 154 (line 273 in version 4.9.5) $\Rightarrow$

$\frac{dE}{dx} *= \frac{2 \pi m_e c^2 r_e^2 z^2}{\beta^2} \rho_e \;\;\;\; \rho_e \propto \frac{NZ}{A}$

Energy Dependence

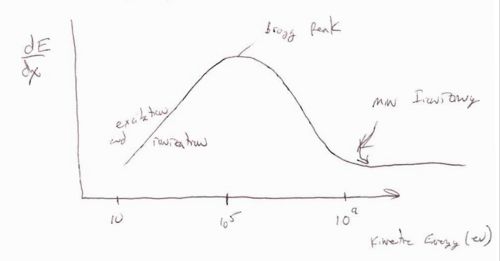
The above curve shows the energy loss per distance traveled ($\frac{dE}{dx}$) as a function of the incident particles energy. There are three basic regions. At low incident energies ( < 10^5 eV) the incident particle tends to excite or even ionize the atoms in the material it is penetrating. The maximum amount of energy loss per distance traveled is defined as the Bragg peak. The region after the Bragg peak, in which the energy loss per distance traveled reaches its smallest value, is refered to as the point of minimum ionizing. Minimimum ionizing particles will have incident energies corresponding to this value or larger. The characteristic of the minimum ionizing particles is that their energy loss per distance traveled is essentially constant making simulations easier until the particle's energy drops below the minimum ionizing energy level as it passes through the material.

In general the Bethe-Bloch equation breaks down at low energies (below the Bragg peak) and is a good description (to within 10%) for

$10 \frac{MeV}{a.m.u.} \lt E \lt 2 \frac{GeV}{a.m.u.}$ and $Z$ < 26 (Iron) : a.m.u = Atomic Mass Unit

the $\frac{1}{\beta^2}$ term in the Bethe-Bloch equation dominates between the Bragg peak and the minimum ionization region.

the $\ln$ term and its corrections influence the dependence of $\frac{dE}{dx}$ as you move up in energy beyond the minimum ionization point.

Energy Straggling

While the Bethe-Bloch formula gives you a way to quantify the amount of energy a heavy charged particle loses as a function of the distance traveled, you should realize that when you calculate the total energy lost via

$\Delta E = \int_{E_i}^{E_f} \left ( \frac{dE}{dx} \right ) dx$

you are only determining the AVERAGE energy loss. In other words, Bethe-Bloch is the Astochastic process describing energy loss.

In reality the energy loss process is a stochastic process because of the statistical fluctuations which occur in the actual number of collisions which take place.

Thick Absorber

A thick absorber is one in which a large number of collisions takes place. In this situation the central limit theorem from statistics tells you that the larger the number of random variable samples , $N$, involved the more the observable will follow a Gaussian distribution. The Gaussian distribution is a good approximation to the binomial distribution when the number of trials is large.

Forest_ErrAna_StatDist#Binomial_with_Large_N_becomes_Gaussian

, and to a Poisson distribution when the mean is a lot larger than 1.

Forest_ErrAna_StatDist#Gaussian_approximation_to_Poisson_when

The gaussian probability function is defined as

$P(x,\Delta) \propto e^{\frac{(\Delta - \bar{\Delta})^2}{ \sigma^2}}$

where the Full Width at Half Max (FWHM) of the distribution = $\left ( 2 \sqrt{2 \ln 2} \right ) \sigma$

In the case of energy loss, the variance using the Bethe-Bloch equation should be

$\sigma_0^2 = 4 \pi N r_e^2 (m_e c^2)^2 \rho \frac{Z}{A} x$

the realitivistic variance is

$\sigma^2 = [\frac{1-\beta^2/2}{1-\beta^2} ]\sigma_0^2$

for very thick absorbers see

C. Tschaler, NIM 64, (1968) 237 ; ibid, 61, (1968) 141

When simulating energy loss of heavy charged particles the Bethe-Bloch equation may be used to calculate a $\frac{dE}{dx}$ which can determine the average energy loss at the given kinetic energy of the particle. This average is then smeared according to a gaussian distribution of variance

$\sigma^2 =4 \pi N r_e^2 (m_e c^2)^2 \rho \frac{Z}{A} x [\frac{1-\beta^2/2}{1-\beta^2} ]$

Thin Absorbers

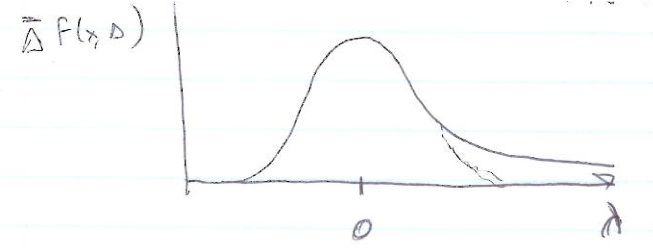
In thin absorbers the number of collisions is small preventing the use of the central limit theorem to describe the stochastic process of energy loss in terms of a Gaussian distribution. The large energy transfers that are possible cause the energy loss distribution to look like a Gaussian with a high energy tail (or foot).

The skewness of the resulting energy loss distribution is quantified as

$\kappa = \frac{\bar{\Delta}}{W_{max}}$

$\Delta \equiv 2 \pi N_a r_e^2 m_e c^2 \rho \frac{Z}{A} \left ( \frac{z}{\beta}\right)^2 x$ = lead term in Bethe Bloch equation

$\rho$ = density of absorbing material.

$W_{max} = \frac{(pc)^2}{\frac{1}{2} \left [ m_e c^2 + \left ( \frac{M^2 c^2}{m_e} \right ) \right ] + \sqrt{(pc)^2 + (Mc^2)^2}}$ = max energy transfered in 1 collision (headon / knock out collision)

This comes from the relativistic kinematics of an Elastic Collision.

$\gamma = \frac{E_{tot}}{Mc^2} = \frac{ \sqrt{(pc)^2 + (Mc^2)^2}}{Mc^2}$

$\beta= \frac{pc}{\gamma Mc^2} = \frac{pc}{E_{tot}}$

$E_k = E_{tot} - Mc^2 = \gamma Mc^2 - Mc^2 = (\gamma - 1 ) Mc^2$

$E_k = \sqrt{(pc)^2 + (Mc^2)^2} - Mc^2$

$(p^{\prime}c)^2 = E_k^2 + 2E_km_ec^2$

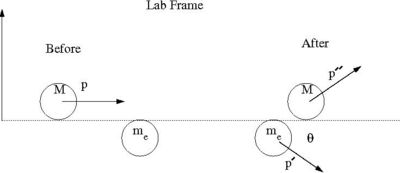
Conservation of Momentum $\Rightarrow$ :

$\vec{p} = \vec{p}^{\; \prime \prime} + \vec{p}^{\; \prime}$

Conservation of Energy $\Rightarrow$ :

$E_{tot} + m_ec^2 = E_{tot}^{\prime \prime} + E_{tot}^{\prime}$

$\sqrt{(pc)^2 + (Mc^2)^2} + m_ec^2 = \sqrt{(p^{\; \prime \prime} c)^2 + (Mc^2)^2} + E_k + m_e c^2$

using conservation of E & P as well as substituting for $p^{\prime}$ you can show

$(p^{\; \prime \prime}c)^2 = (pc)^2 - 2E_k\sqrt{(pc)^2 +(Mc^2)^2} + E_k^2$ : cons of E

$= (pc)^2 + E_k^2 + 2E_km_ec^2 -2pc\sqrt{E_k^2+2E_km_ec^2} \cos(\theta)$ : cons of P

$\Rightarrow$

$pc \cos(\theta) \sqrt{1+\frac{2m_ec^2}{E_k}} = \sqrt{(pc)^2+(Mc^2)^2} + m_ec^2$

solving for $E_k$

$E_k = \frac{2m_ec^2(pc)^2\cos^2 (\theta)}{[\sqrt{(pc)^2 + (Mc^2)^2} +m_ec^2]^2 - (pc)^2 \cos^2 (\theta)}$

(Landau Theory)

$\kappa \leq 0.01$

Landau assumed

1. $W_{max} = \infty$ is max energy transfer
2. electrons are free (energy transfer is so large you can neglect binding)
3. incident particle maintains velocity (large momentum transfer from big mass to small mass) (bowling ball hits ping pong ball)

L. Landau, "On the Energy Loss of Fast Particles by Ionization", J. Phys., vol 8 (1944), pg 201

instead of a gaussian distribution Landau used

$P(x,\Delta) \propto \frac{1}{\bar{\Delta}\pi} \int_0^{\infty} e^{-u \ln u - u \lambda} \sin(\pi u) du$

where

$\lambda = \frac{1}{\bar{\Delta}} \left [ \Delta - \bar{\Delta} \ln \bar{\Delta} - \ln \epsilon + 1 -C \right ]$

$\bar{\Delta} = 2\pi N_a r_e^2 m_e c^2 \rho \frac{Zz^2}{A \beta^2}x$

$\ln \epsilon = \ln \left [ \frac{(1-\beta^2)I^2}{2m_ec^2 \beta^2} \right ]$

$C = 0.577$

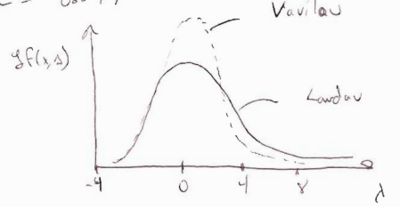
(Vavilou's Theory)

Vavilous paper

P.V. Vavilou, "Ionization losses of High Energy Heavy Particles", Soviet Physics JETP, vol 5 (1950? )pg 749

describe the physics for the case

$0.01 \lt \kappa \lt \infty$

The distribution function derived is shown below as well as a conceptual overlay of Vavilou's and Landau's distributions. (The $\zeta f(x,\Delta)$ in the picture should be a $\bar{\Delta}P(x,\Delta)$ )

$P(x,\Delta) = \frac{1}{\bar{\Delta}\pi} x e^{x(1+\beta^2C)} \int_0^{\infty} e^{xf_1} \cos(y \lambda_1 + xf_2) dy$

where

$f_1 = \beta^2 \left [ \ln(y) - C_i(y)\right ] - \cos(y) - y S_i(y)$

$f_2 = y\left [ \ln(y) - C_i(y)\right ] + \sin(y) + \beta^2 S_i(y)$

$C_i(y) \equiv - \int_y^{\infty} \frac{\cos(t)}{t} dt$

$S_i(y) \equiv \int_0^{y} \frac{\sin(t)}{t} dt$

$C = 0.577$

GEANT4's implementation

GEANT 4 uses the skewness parameter $\kappa$ to determine if it will use a "fluctuations model" to calculate energy straggling or the gaussian model described in section 3.2.1.

kappa > 10

If

$\kappa \equiv \frac{ \bar{\Delta}}{W_{max}}$ > 10

and we have a thick absorber ( large step size) then the Gausian function in 3.2.1 is used to calculate energy straggling.

What happens is $\Delta E$ is calculated via $\int_{E_i}^{E_f} \frac{dE}{dx} dx$ then the actual energy loss predicted by the simulation is chosen from a Gaussian distribution to account for energy straggling such that the $\sigma$ of this Gaussian distribution is given by:

$\sigma^2 = 2 \pi r_e^2m_ec^2N_{el} \frac{Z_h}{\beta^2} T_C s (1 - \frac{\beta^2}{2})$

where

$N_{el}$ = electron density of the medium

$Z_h$ = charge of the incident particle

$s$ = step size

$T_C$ = cutoff kinetic energy for $\delta$-electrons

$T_C$ tells GEANT where to put the cutoff for using the Gaussian distribution for energy straggling. This tells the simulation the low energy cutoff where Bethe-Bloch starts to fail due to ionization.

Delta-electrons

What is a $\delta$ - electron?

$\delta$ - electrons are also known as "knock -on" electrons and delta rays.

As heavy particles traverse a medium they can ionize electrons from atoms. The ejected electrons ($\delta$ - electrons) can be given enough energy to ionize as well.

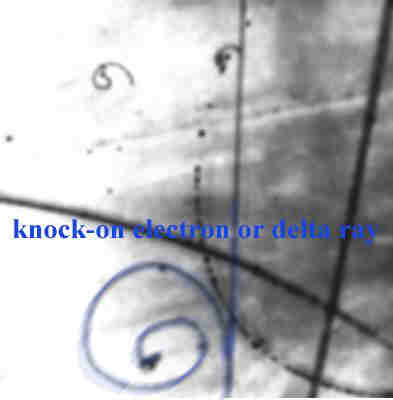
In a cloud chamber (a supercooled volume of super saturated water vapor which ionizes as charged particles pass through) such and event would look like:

The blue spiral in the above gas chamber picture is a high energy electron ejected from a collision that spirals in the B-field ejecting low energy electrons at the end. The B-field is directed out of the picture.

The physics of ionization is different from the physics used to calculate Bethe-Bloch energy loss. Remember Bethe-Bloch starts to break down at low energies below the Bragg peak.

Because of this GEANT 4 sets the cutoff for this process to be

$T_{cut}$ > 1 keV

Note: The BE energies of an electron in Hydrogen is 13.6 ev and the electrons in Argon have binding energies between 15.7 eV and 3.2 keV.

Fluctuations Model: kappa < 10

If $\kappa \equiv \frac{ \bar{\Delta}}{W_{max}} \lt \frac{\Delta E}{T_C}$

Then GEANT 4 uses a "Fluctuations Model" to determine energy loss instead of Bethe-Bloch.

Fluctuations Model

1. the atom is assumed to have 2 energy levels $E_1$ and $E_2$
2. you can excite the atom and lose either $E_1$ or $E_2$ or you can ionize the atom and lose energy according to a $\frac{1}{E^2}$ function $u_j$.

The total energy loss in a step will be

$\Delta E = \Delta E_{exc} + \Delta E_{ion}$

where

$\Delta E_{exc} = \eta_1 E_1 + \eta_2 E_2$

$\Delta E_{ion} = \sum_{j=1}^{\eta_3} \frac{I}{1 - u_j \frac{T_{up}-I}{T_{up}}}$

$\eta_1$, $\eta_2$, and $\eta_3$ are the number of collisions which are sampled from a poison distribution

$u_j = \int_{I}^{E_j} \frac{I T_{up}}{T_{up} - I} \frac{dx}{x^2}$

$E_j = \frac{I}{1- rand \frac{T_{up}-1}{T_{up}}}$ : rand = random number between 0 and 1

$T_{up} = \left \{ {~ 1 keV \; threshold \;energy \;for \; \delta- ray \; production \atop T_{max} \; \;\;\; if \; T_{max} \lt 1 keV} \right .$

$I$ = mean ionization energy

$E_2 \approx (10 eV) Z^2$

$\ln E_1 = \frac{\ln (I) - f_2 \ln (E_2)}{f_1}$

$f_1 + f_2 =1$

$f_2 =\left \{ {0 \; z=1 \atop \frac{2}{z} \; z \ge 2} \right .$

The fluctuation model was comparted with data in

K. Lassila-Perini and L. Urban, NIM, A362 (1995) pg 416

The cross sections used for excitation and ionization may be found in

H. Bichel, Rev. Mod. Phys., vol 60 (1988) pg 663

Range Straggling

Def of Range (R)

The distance traveled before all the particles energy is lost.

$R \equiv \int_0^T \frac{dE}{\frac{dE}{dx}}$

= theoretical calculation of the path length traveled by a particle of incident energy $T$

Note units: $\left [ R \right ] = \frac{g}{cm^2} ; \left [ \frac{dE}{dx} \right ] = \frac{MeV \cdot cm^2}{g}$

the Energy Straggling introduced in the previous section can explain why identical particles penetrate material to different depths. The energy straggling results in Range straggling.

If we do a shielding experiment where we have a source of incident particles of energy E and we count how many "punch" through a material of thickness (x) we would see a transmission coefficient $\left ( \frac{N_{out}}{N_{in}} \right)$ which would look like

Fractional Range Straggling

$\frac{\sigma_R}{R} \equiv$ fractional range straggling

Assuming the energy loss of a non-relativistic heavy ion through matter follows a Gaussian (thick absorber)

Then it can be shown that

$\frac{\sigma_R}{R} \approx \frac{1}{2} \sqrt{\frac{M}{A}}$

where

$M$ = mass of the target electrons

$A$ = atomic mass of the Projectile

since

$m_e = 9.11 \times 10^{-31}$ kg

and

1 a.m.u. = $1.66 \times 10^{-27}$ kg

then

$\frac{\sigma_R}{R} \approx \frac{1}{2} \sqrt{\frac{9.11 \times 10^{-31}}{1.66 \times 10^{-27}A}}$

= 1.17 % if using a proton (A=1)

The above is a "back of the envelope" estimate. The experimentally measured values for Cu, Al, and Be target using a proton projectile are

If the incident projectile is an electron then $\frac{\sigma_R}{R} \approx \frac{1}{2}$ making electron range straggling a vague concept.

There are several definitions of electron range

1.) Maximum Range ($R_0$)

This range is defined using the continuous slowing down approximation (CSDA) where electrons are assumed to have many collisions over very small distances making it appear to be continuous energy loss instead of discrete. The range is then calculated by integrating over these average energy losses $\frac{dE}{dx} \cdot s$.

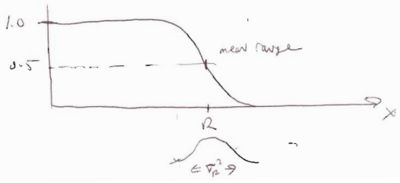
2.) Practical Range ($R_P$)

This stopping distance is defined by extrapolating the electron transmission curve to zero (see below).

Electron Capture and Loss

Bohr Criterion

"A rapidly moving nucleus is fully ionized if its velocity exceeds that of its most tightly bound electron"

The Bohr Model:

$\Rightarrow E = \frac{mz^2e^4}{8 \epsilon_0^2 h^2 n^2}$

for the inner most electron ($n=1$)

Electron K.E. = $\frac{1}{2} mv^2 = \frac{mz^2e^4}{2(4\pi \epsilon_0)^2 \hbar^2} \Rightarrow v = \frac{z e^2}{4 \pi \epsilon_0 \hbar}$

the fine structure constant $\alpha \equiv \frac{e^2}{4 \pi \epsilon_0 \hbar c} = \frac{1}{137}$

$v = zc \alpha$

If $v \gt zc \alpha$ the nucleus is fully ionized

or

if $\frac{z}{v/c} = \frac{z}{\beta} \lt \frac{1}{\alpha} = 137$

alternatively if the ion is moving through a material with a speed such that

$\frac{z}{\beta} \gt \frac{1}{\alpha} =137$

Then electrons may be captured by the projectile and lost by the target.

Z-effective

Describing the charge state of your heavy ion traveling through matter at a velocity below the Bohr criterion is very complicated. There is a competition between electron capture and loss. Accurate cross sections are needed to simulate the process reliably.

Some insight into this process can be found using the Thomas-Fermi model

$V \propto \frac{Ze^{-r/a}}{r}$

to describe an atom moving slow enough so it has captured many electrons but fast enough so its not neutral. In the Thomas-Fermi model the distribution of electrons in an atom is described as being uniformly distributed such that there are 2 electrons in each discrete volume of phase space( the space in which all possible states of a system are represented) defined using planks constant as $h^3$.

For the purpose of simulations you would like a relationship for $Z_{eff}$ in terms of $\beta$ and $Z$.

It is usually adequate to use fits for empirical data as long as we know that we are in the kinematic range in which those fits are valid.

when $E \lt 10$ MeV the data indicates that

$Z_{eff} = Z(1 - e^{-\beta\frac{B}{Z^{2/3}}})$

where

$B = 130 \pm 5$

$Z_{eff} \equiv$ effective charge f the projectile = $Z - \bar{q}_c$

$Z$ = number of protons

$\bar{q}_c$ = average number of captured electrons

When calculating stopping power for E < 10 MeV you use $Z_{eff}$ in the Bethe-Bloch equation.

Note: As the ions charge state fluctuates while it slows down (or if accelerated through materials) you will need to recalculate the energy loss, and as a result you will get larger energy loss fluctuations in this energy range.

For thin absorber you will look for stripping and loss cross sections.

Here a thin absorber is one whose thickness is less than the charge equilibrium distance defined as the distance traveled until the projectile's velocity is $v \ll zc\alpha$

A rule of thumb is that a thin absorber for low energy ions has a thickness $\le \frac{5 \frac{\mu g}{cm^2}}{\rho}$

For thick absorbers: The experimentally determined expression for the change in $Z_{eff}$ from $Z$ is

$\Delta Z_{eff} = \frac{1}{2} \sqrt{ \left [ Z_{eff} \left (1 - \frac{Z_{eff}}{Z} \right )^{1.67}\right ] }$

Multiple Scattering

The Bethe-Bloch equation tells us how much energy is lost and GEANT4s calculation of this energy is described above.

Now we need to know which direction the scattered particle goes after it has lost this energy.

The work of Moliere describes the angular deflection of the particle which lost the energy thereby leading to a prediction of the Cross-section. GEANT4 though uses the more complete Lewis theory to describe Multiple Coulomb Scattering (MCS) sometimes generically referred to as multiple scattering.

There are 3 regions in which coulomb scattering is calculated

1.) Single Scattering

For thin materials.

If the probability of more than 1 coulomb scattering is small

Then use the Rutherford formula for $\frac{d \sigma}{d \Omega}$

2.)Multiple Scattering

In this case the number of independent scatterings is large (N > 20) and the energy loss is small such that the problem can be treated statisticaly to obtain a probability distribution for the net deflection angle $[P(\theta)]$ as a function of the material thickness that is traversed.

3.) Plural Scattering

If 1< N $\le$ 20 then you can't use Rutherford to describe the scattering nor use a normal random statistical description.

see E. Keil, Z. Naturforsch, vol 15 (1960), pg 1031

Reviews of rigorous multiple scattering calculations may be found in

P.C. Hemmer, et. al., Phys. Rev, vol 168 (1968), pg 294

GEANT4's implementation of MSC (N>20)

GEANT4 models MSC when N>20 using model functions to determine the angular and spatial distributions chosen to give the same moments of these distributions as the Lewis theory.

H.W. Lewis, Phys. Rev., vol 78 (1950), pg 526

modern versions of the above are at

J.M. Fernandez-Varea, et. al., NIM, B73 (1993), pg 447

I. Kawrakow, et. al., NIM, B142 (1998) pg 253

When N>20 multiple scattering can be described as a statistical process using a modified version of the Boltzman transport equation from statistical mechanics.

Note

The simulation step size is chosen such that (N>20), If you have materials so thin that N < 20 then GEANT4 will likely skip the material. (one way around this is to increase the thickness and change the density). If the material thickness can't be increased because its sandwhiched between two other materials then you will need to write a special step algorithm for the volume and have GEANT4 use it for the step.

Let $f(s,\vec{x},\hat{v}) \equiv$ the distribution function for a system of incident particles traveling through a material.

where

$s =$ arc length of the particle's path through the material

$\vec{x} =$ position of a charged particle

$\hat{v} =$ direction of motion of the particle $\frac{\vec{v}}{|\vec{v}|}$

The multiple scattering experienced by a single charged particle traveling through the material is then simulated by sampling from the distribution $f(s,\vec{x},\hat{v} )$

The governing transport/diffusion equation is based on the continuity equation but with a "sink" term representing the possibility of collisions ejecting particles out of the volume.

$\frac{\partial f(s,\vec{x},\hat{v} ) }{\partial s} + \hat{v} \bullet \vec{\nabla}f(s,\vec{x},\hat{v} ) = N \int \sigma(\hat{v} \bullet\hat{v}^{\prime} )\left [ f(s,\vec{x},\hat{v}^{\prime} ) - f(s,\vec{x},\hat{v} ) \right ] d \hat{v}^{\prime}$

where

$N$ = number of atoms per volume

$\sigma(\hat{v} \bullet\hat{v}^{\prime} )$ = cross sections for elastic scattering per Solid angle $\left ( \frac{d \sigma}{d \Omega} \right )$

To solve the above diffusion equation the distribution function, $f(s,\vec{x},\hat{v} )$ is expanded in Spherical Harmonics ( $Y_{\ell}^m(\theta,\phi)$ ) and $\sigma$ expand in Legendre Polynomials ($P_N(cos \theta)$) since it has no $\phi$ angle dependence.

Note

For Coulomb Scattering in polar coordinates you can write the potential in terms of Legendre Polynomials such that:

$U=k \frac{q}{r}$

= $k\frac{q}{\sqrt{r^2-a^2-2ar \cos \theta}}$ in polar coordinates

= $k\frac{q}{r} \sum_{n=0}^{\infty} P_n(\cos \theta) \left ( \frac{a}{r}\right )^n$ (the sqrt term above is expanded using binomial series

$f(s,\vec{x},\hat{v} ) = \sum_{\ell,m} f_{\ell,m}(\vec{x},s) Y_{\ell}^m(\hat{v})$

after substituting into the diffusion equation and doing the integral on the righ hand side you get

$\frac{\partial f_{\ell,m}(\vec{x},s) }{\partial s} + \frac{f_{\ell,m}(s,\vec{x},\hat{v} }{\lambda_{\ell}} = - \sum_{\lambda, i, j} \vec{\nabla} f_{i,j}(\vec{x},s ) \bullet \int Y_{\ell,m}^{\star} \hat{v} Y_{i,j} d \hat{v} \; \; \; \; \; \; \; \;\hat{v} = f(\theta.\phi)$

where

$\frac{1}{\lambda_{\ell}} = 2 \pi N \int_0^{\pi} \left [ 1-P_{\ell}(\cos \theta)\right ] \sigma(\theta) \sin(\theta) d \theta$ = $\ell^{th}$ transport mean free path for the $f_{\ell}$ distribution function ( $\phi$ symmetry is assumed making it $m$ independent)

From the above one can find the average distances traveled and the average deflection angle of the distribution. Again, see :

J.M. Fernandez-Varea, et. al., NIM, B73 (1993), pg 447

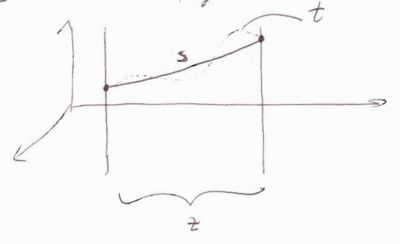
The "moments" of $f(s,\vec{x},\hat{v})$ are defined as

$\lt z\gt = 2 \pi \int z f(s,\vec{x},\hat{v}) \sin(\theta) d \theta d |\vec{x}| = \lambda_1 \left [ 1-e^{-s/\lambda_1}\right ]$ = mean geometrical path length

$\lt \cos(\theta)\gt = 2 \pi \int_{-1}^1 \sum_{\ell} P_{\ell}(\cos \theta) \int f(s,\vec{x},\hat{v}) \sin(\theta) d \theta d |\vec{x}| = e^{-s/\lambda_1}$

$\frac{1}{\lambda_1} = 2 \pi N \int_0^{\pi} \left [ 1-P_1(\cos \theta)\right ] \sigma(\theta) \sin(\theta) d \theta$

Notice there are 3 lengths

$s$ = geometrical path length between endpoints of the step =$\left \{ {line \; if \; \vec{B} = 0 \atop arc \; if \; \vec{B} \ne 0 } \right .$

$t$ = true path length = actual length of the path taken by particle

$\lt z\gt$ - mean geometrical path length along the z-axis

In GEANT4 the $\lambda_{\ell}$'s are taken from

If 100 eV < K.E. of electron or positron < 10 MeV

D. Liljequist, J. Applied Phys, vol 62 (1987), 342

J. Applied Phys, vol 68 (1990), 3061

If K.E. > 10 MeV

R. Mogol, Atomic Data, Nucl, Data tables, vol 65 (1997) pg 55

with <z> now known GEANT will try to determine "$t$" for the energy loss and scattering calculations.

A model is used for this where

$t=\frac{1}{\alpha} \left [ 1 - (1- \alpha \omega z)^{\frac{1}{\omega}})\right ]$

where

$\omega = 1 + \frac{1}{\alpha \lambda_{10}}$

$\alpha =\left \{ {\frac{\lambda_{10} - \lambda_{11}}{s \lambda_{10}}\;\;\;\; K.E. \ge M_{particle} \atop \frac{1}{R}\;\;\;\; K.E. \lt M_{particle}} \right .$

$s$ = stepsize

$\lambda_{10} - \frac{\lambda_1}{1-\alpha s}$

$\lambda_{11} = \lambda_1$ at end of strep

while $\lt cos \theta \gt$ is calculable, GEANT4 evaluates $\cos (\theta)$ from a probability distribution whose general form is

$g[\cos(\theta)] = p \left ( qg_1[\cos(\theta)] + (1-q)g_3[\cos(\theta)] \right ) + (1-p)g_2[\cos(\theta)]$

where

$g_1(x) = C1e^{-a(1-x)}$

$g_2(x) = \frac{C_2}{(b-x)^d}$

$g_3(x) = C_3$

$C_1, C_2, C_3$ are normalization constants

$p,q,a,b,d$ are parameters which follow the work reported in

V.L. Highland, NIM, vol 219 (1975) pg497

The GEANT4 files in version 4.8 were located in

/source/processes/electromagnetic/utils/src/G4VMultipleScattering.cc

and

/source/processes/electromagnetic/standard/src/G4MscModel.cc

/source/processes/electromagnetic/standard/src/G4MultipleScattering.cc

Simulations_of_Particle_Interactions_with_Matter