Difference between revisions of "A W thesis old"

From New IAC Wiki
Jump to navigation Jump to search
 
Line 1: Line 1:
 +
=Results and Conclusion=
 +
This thesis set out to measure the detection limit improvement of coincidence photon activation analysis over the more common photon activation analysis method. By requiring detected photons to be in coincidence, it is thought that the detection limit can be improved over standard PAA. The following sections contain the results obtain performing singles and coincidence counting for PAA.
 +
 +
 +
==Detection Limit of PAA for a Yt-89 foil==
 +
 +
 +
 +
The detection limit represents a quantitative measurement of the lowest number of nuclei that may be observed.  This quantity may be expressed in units of parts-per-million (PPM) or in the equivalent units of (<math>\mu g/g</math>).
 +
 +
The concept of photon activation analysis relies on activating a nucleus by using a high energy photon to eject one or more nucleons (protons or neutrons).  The nuclei that have had one or more nucleons removed are typically unstable and decay.  One can determine this rate of decay in terms of the probability of decay , <math>\lambda.</math>.  If I let N(t) represent the number of radioactive nuclei at time t I can estimate the change in this number by
 +
 +
===Radioactive decay===
 +
 +
:<math>N(t) -N(t + \Delta t) = N(t) (\lambda \Delta t)</math>
 +
 +
dividing by <math>\Delta t</math> and taking the limit of <math>\Delta t \rightarrow 0</math>
 +
:<math>\Rightarrow \lim_{\Delta t \rightarrow 0} \frac{N(t+\Delta t) - N(t) }{\Delta t} = \frac{dN}{dt} = - \lambda N(t)</math>
 +
 +
The solution to the above differential is
 +
 +
:<math>N(t) = N_0 e^{\lambda t}</math>
 +
 +
If I want to know the time required until the original number of activated nuclei (<math>N_0</math>) has been cut in half
 +
 +
:<math>\Rightarrow \frac{1}{2} = e^{\lambda t_{1/2}} \Rightarrow  t_{1/2} = \frac{\ln 2}{\lambda}</math>
 +
 +
The half life of a decaying nucleus is inversely proportional to the probability of decay.
 +
 +
The activity<math> (A)</math> of a sample of radioactive nuclei is defined as the rate of the decay and is given by
 +
 +
:<math>A = \lambda N(t)</math>
 +
 +
The above has the units of decays per sec , or Bacquerel.
 +
 +
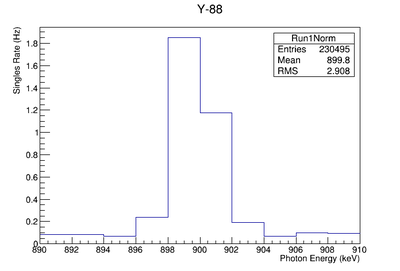
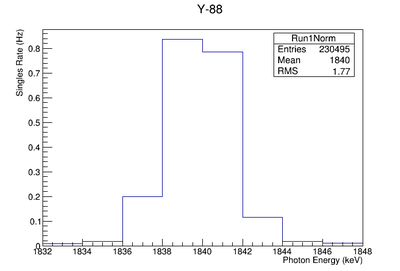
The nucleus Y-88 for example has a half life of 106.6 days.  If I measure the activity of the sample at time <math>t</math> then the number of radioactive nuclei at time <math>t</math> is given by
 +
 +
 +
: <math>N= A \frac{t_{1/2}}{\ln 2} = \left ( 1.33 \times 10^7 \mbox {s} \right ) A</math> 
 +
 +
where <math>A</math> is the number of measured decays per sec.
 +
 +
The isotope Y-88 was produced by ejecting a neutron from the stable Y-89 nucleus using a photon having more energy enough energy to overcome the binding energy.
 +
 +
Neutron Separation Energy=<math>S_n = B({A \atop Z} X_{N})-B({{A-1} \atop Z} X_{N-1})</math>
 +
 +
<math>B({89 \atop39} Y_{50}) = 775538.048 keV</math>
 +
<math>B({88 \atop39} Y_{49}) = 764061.688 keV</math>
 +
:<math>S_n = B({89 \atop 39} X_{50})-B({{88} \atop 39} Y_{49})=775538.048-764061.688=11.47636</math> MeV
 +
A photon needs to have at least 11.5 MeV of energy to eject one neutron from Y-89.
 +
 +
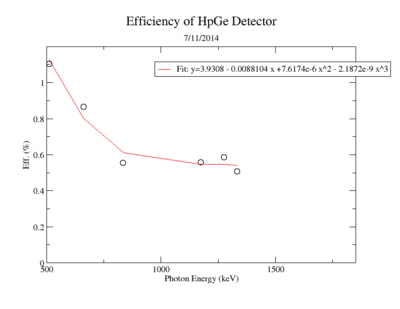
To determine the number of Y-89 atoms that were converted you need to know the efficiency of the detector (<math>\epsilon</math>), the branching ratio of the photons measured (Br), and the probability of creating Y-88 from Y-89.  The detector efficiency for measuring a 898 keV photon using an HpGe detector was  (0.7830 +/- 0.0471) % and ( 0.3119 +/- 0.0310) % for 1836.1 keV photons.  The Y-88 activity was extrapolated to be 300 Hz using the known half life and the observed efficiency corrected count rate in a HpGe detector.  The branching ratio for the 898 keV line is almost unity (95 %) indicating that after irradiation there were 300 Y-88 nuclei decaying per second or
 +
:: <math>N= A \frac{t_{1/2}}{\ln 2} = \left ( 1.33 \times 10^7 \mbox {s} \right ) 300 Hz = 4 \times 10^{9}</math>  activated Nuclei.
 +
 +
To determine how many Y-89 atoms had a neutron removed we would need to know what fraction of all the photon induced reaction are single neutron knockout. 
 +
 +
The number of atoms in a Yt foil having a mass of <math>0.0496 \pm 0.002</math> g is
 +
 +
: <math>n_{Y-89} = (0.0496 \pm 0.002 g) \times \left ( \frac {1 \mbox{mole}}{88.90585 \mbox{g}}\right ) \times \left ( \frac {6 \times 10^{23}  \mbox{atoms}}{ \mbox{mole}}\right ) = 3.35 \times 10^{20}</math> atoms
 +
 +
==Activation efficiency for Y-88==
 +
 +
It is well understood that radioactive materials decay as an exponential function of time. We can therefore use the measured signals of the Y-88 sample fitted to an exponential curve to find the initial number of atoms in the foil. The exponential fit was extrapolated back to the initial time t=0 when the foil was activated. We want to convert this initial rate (Hz) into units of Curie. The half-life of Y-88 is well know, 106.63 days, and was used to calculate the decay constant <math>\lambda</math>. Using the relationship between activity and the number density <math>A=\lambda N</math> we can find <math>N_0</math> for t=0.
 +
 +
The yttrium foil's mass was weighted at the IAC and found to be 0.0288 +/- 0.0002 g. Using Avogadro's number, <math>N_a</math>, and the isotopic mass of Y-89, <math>m_i=88.905848 \frac{g}{mol}</math>, we can plug into the following equation: <math>Number of atoms = \frac{mN_a}{m_i}</math>. The foil is predicted to contain  <math>1.95\times 10^{20} \pm 1.35\times 10^{18}</math> atoms of Y-89.
 +
 +
Taking to ratio of <math>N_0</math> and the number of atoms will measure the accelerator beam's efficiency at activating the sample. Using the above number of atoms and using the average <math>N_0</math> found previously, we get a ratio of <math> (19.7 \pm 2.72) \times 10^{-12}</math>.
 +
 +
 +
----------------
 +
 +
During activation of the Y-90 sample, a neutron can be knocked out of the Y-90 nucleus leaving behind the Y-88 nucleus in an excited state.  The Y-88 nucleus has a decay half life of 106.63 days.  During the irradiation you have two competing processes, the knocking out of a neutron to make Y-88 and the decay of Y-88 while you are activating it.
 +
 +
==Determining the lowest measurable activity==
 +
 +
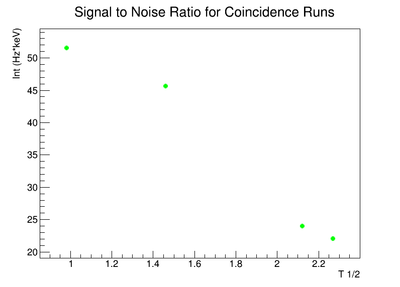
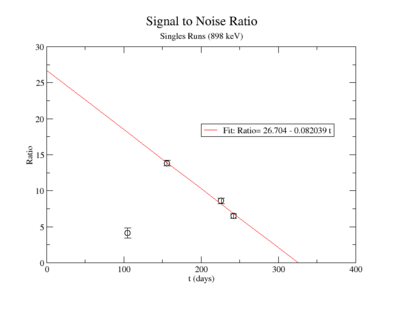
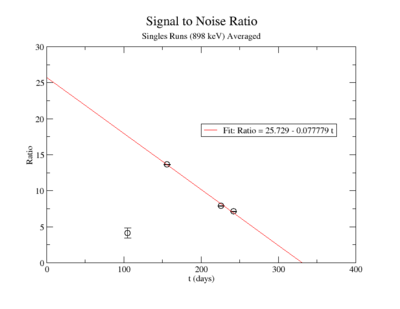
The lowest activity of Y-88 that the apparatus could measure is predicted by extrapolating the measured signal to noise ratio forward in time until it is zero. The signal to noise ratio fits shown in figureXX.YY were used for this extrapolation. Beyond this point in time, we will not be able to distinguish the signal from the background noise and measurements will no longer be possible with this apparatus. This time for the SNR to be zero was used in the exponential decay function <math>N(t)=N_0e^{-\lambda t}</math> to find the lowest measurable activity, <math> N(t_{final}) </math>.  This activity is reported in Table XX.III  for singles and coincidence measurements of both photon energies.
 +
 +
 
=Apparatus=
 
=Apparatus=
  

Latest revision as of 17:37, 5 May 2015

Results and Conclusion

This thesis set out to measure the detection limit improvement of coincidence photon activation analysis over the more common photon activation analysis method. By requiring detected photons to be in coincidence, it is thought that the detection limit can be improved over standard PAA. The following sections contain the results obtain performing singles and coincidence counting for PAA.


Detection Limit of PAA for a Yt-89 foil

The detection limit represents a quantitative measurement of the lowest number of nuclei that may be observed. This quantity may be expressed in units of parts-per-million (PPM) or in the equivalent units of ([math]\mu g/g[/math]).

The concept of photon activation analysis relies on activating a nucleus by using a high energy photon to eject one or more nucleons (protons or neutrons). The nuclei that have had one or more nucleons removed are typically unstable and decay. One can determine this rate of decay in terms of the probability of decay , [math]\lambda.[/math]. If I let N(t) represent the number of radioactive nuclei at time t I can estimate the change in this number by

Radioactive decay

[math]N(t) -N(t + \Delta t) = N(t) (\lambda \Delta t)[/math]

dividing by [math]\Delta t[/math] and taking the limit of [math]\Delta t \rightarrow 0[/math]

[math]\Rightarrow \lim_{\Delta t \rightarrow 0} \frac{N(t+\Delta t) - N(t) }{\Delta t} = \frac{dN}{dt} = - \lambda N(t)[/math]

The solution to the above differential is

[math]N(t) = N_0 e^{\lambda t}[/math]

If I want to know the time required until the original number of activated nuclei ([math]N_0[/math]) has been cut in half

[math]\Rightarrow \frac{1}{2} = e^{\lambda t_{1/2}} \Rightarrow t_{1/2} = \frac{\ln 2}{\lambda}[/math]

The half life of a decaying nucleus is inversely proportional to the probability of decay.

The activity[math] (A)[/math] of a sample of radioactive nuclei is defined as the rate of the decay and is given by

[math]A = \lambda N(t)[/math]

The above has the units of decays per sec , or Bacquerel.

The nucleus Y-88 for example has a half life of 106.6 days. If I measure the activity of the sample at time [math]t[/math] then the number of radioactive nuclei at time [math]t[/math] is given by


[math]N= A \frac{t_{1/2}}{\ln 2} = \left ( 1.33 \times 10^7 \mbox {s} \right ) A[/math]

where [math]A[/math] is the number of measured decays per sec.

The isotope Y-88 was produced by ejecting a neutron from the stable Y-89 nucleus using a photon having more energy enough energy to overcome the binding energy.

Neutron Separation Energy=[math]S_n = B({A \atop Z} X_{N})-B({{A-1} \atop Z} X_{N-1})[/math]

[math]B({89 \atop39} Y_{50}) = 775538.048 keV[/math] [math]B({88 \atop39} Y_{49}) = 764061.688 keV[/math]

[math]S_n = B({89 \atop 39} X_{50})-B({{88} \atop 39} Y_{49})=775538.048-764061.688=11.47636[/math] MeV

A photon needs to have at least 11.5 MeV of energy to eject one neutron from Y-89.

To determine the number of Y-89 atoms that were converted you need to know the efficiency of the detector ([math]\epsilon[/math]), the branching ratio of the photons measured (Br), and the probability of creating Y-88 from Y-89. The detector efficiency for measuring a 898 keV photon using an HpGe detector was (0.7830 +/- 0.0471) % and ( 0.3119 +/- 0.0310) % for 1836.1 keV photons. The Y-88 activity was extrapolated to be 300 Hz using the known half life and the observed efficiency corrected count rate in a HpGe detector. The branching ratio for the 898 keV line is almost unity (95 %) indicating that after irradiation there were 300 Y-88 nuclei decaying per second or

[math]N= A \frac{t_{1/2}}{\ln 2} = \left ( 1.33 \times 10^7 \mbox {s} \right ) 300 Hz = 4 \times 10^{9}[/math] activated Nuclei.

To determine how many Y-89 atoms had a neutron removed we would need to know what fraction of all the photon induced reaction are single neutron knockout.

The number of atoms in a Yt foil having a mass of [math]0.0496 \pm 0.002[/math] g is

[math]n_{Y-89} = (0.0496 \pm 0.002 g) \times \left ( \frac {1 \mbox{mole}}{88.90585 \mbox{g}}\right ) \times \left ( \frac {6 \times 10^{23} \mbox{atoms}}{ \mbox{mole}}\right ) = 3.35 \times 10^{20}[/math] atoms

Activation efficiency for Y-88

It is well understood that radioactive materials decay as an exponential function of time. We can therefore use the measured signals of the Y-88 sample fitted to an exponential curve to find the initial number of atoms in the foil. The exponential fit was extrapolated back to the initial time t=0 when the foil was activated. We want to convert this initial rate (Hz) into units of Curie. The half-life of Y-88 is well know, 106.63 days, and was used to calculate the decay constant [math]\lambda[/math]. Using the relationship between activity and the number density [math]A=\lambda N[/math] we can find [math]N_0[/math] for t=0.

The yttrium foil's mass was weighted at the IAC and found to be 0.0288 +/- 0.0002 g. Using Avogadro's number, [math]N_a[/math], and the isotopic mass of Y-89, [math]m_i=88.905848 \frac{g}{mol}[/math], we can plug into the following equation: [math]Number of atoms = \frac{mN_a}{m_i}[/math]. The foil is predicted to contain [math]1.95\times 10^{20} \pm 1.35\times 10^{18}[/math] atoms of Y-89.

Taking to ratio of [math]N_0[/math] and the number of atoms will measure the accelerator beam's efficiency at activating the sample. Using the above number of atoms and using the average [math]N_0[/math] found previously, we get a ratio of [math] (19.7 \pm 2.72) \times 10^{-12}[/math].


During activation of the Y-90 sample, a neutron can be knocked out of the Y-90 nucleus leaving behind the Y-88 nucleus in an excited state. The Y-88 nucleus has a decay half life of 106.63 days. During the irradiation you have two competing processes, the knocking out of a neutron to make Y-88 and the decay of Y-88 while you are activating it.

Determining the lowest measurable activity

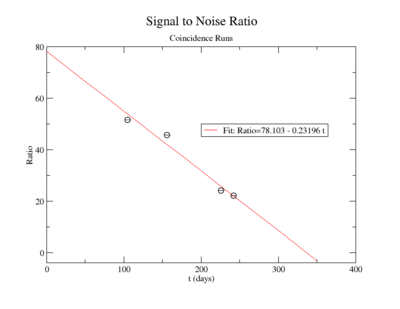
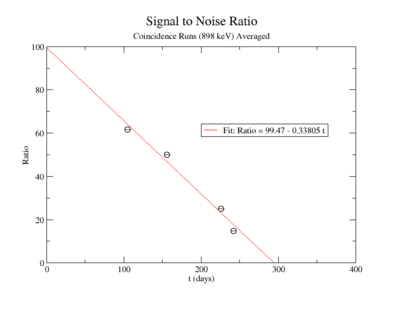
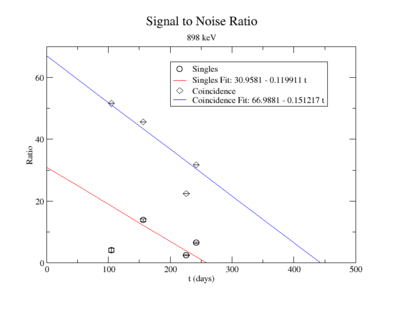
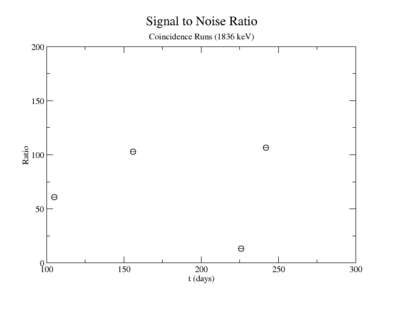
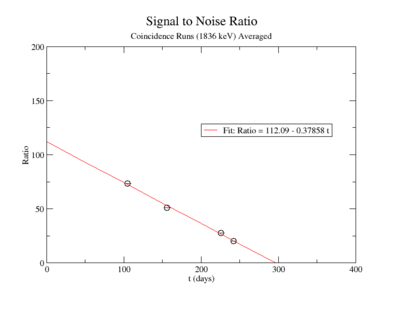
The lowest activity of Y-88 that the apparatus could measure is predicted by extrapolating the measured signal to noise ratio forward in time until it is zero. The signal to noise ratio fits shown in figureXX.YY were used for this extrapolation. Beyond this point in time, we will not be able to distinguish the signal from the background noise and measurements will no longer be possible with this apparatus. This time for the SNR to be zero was used in the exponential decay function [math]N(t)=N_0e^{-\lambda t}[/math] to find the lowest measurable activity, [math] N(t_{final}) [/math]. This activity is reported in Table XX.III for singles and coincidence measurements of both photon energies.


Apparatus

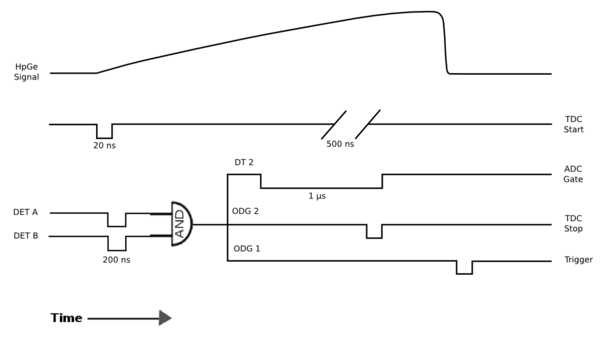
The coincidence counting set-up and modules path are as follows. A source is set atop a base constructed of hydrogen dense blocks. These were chosen to reduce the number of background energy spikes detected. The source is placed an equal distance from decorator A and detector B. Detector A is positioned directly above the source. A high-purity germanium detector is being utilized for this set-up. The one outgoing signal enters a ORTEC 673 Spectroscopy Amplifier and the outgoing signal then passes through a CANBERRA CFD 2035A. The signal can then enter an optional CAEN CFD to produce a time delay, or can pass directly into a channel (1) of the Level Translator. The second outgoing signal from the Spec Amp goes to a peak sensing CAEN V785N. The output from this module goes to the DAQ. Perpendicular from detector A and placed an equal distance from the source is detector B. This detector can either be a NaI-3 or a germanium detector depending on the source being counted. Detector B’s signal goes to a Post Amplifier and one outgoing signal goes to the above mentioned CAEN V785N and also to the DAQ. The second signal enters a CANBERRA CFD 2035A. The outgoing signal goes to a different channel (4) of the same Level Translator. A ribbon cable on the Level Translator module goes to a Time-to-Digital Converter (TDC) CAEN V775 that is operating in common start mode. Both channels (1 and 4) of the Level Translator outgoing signal pass to a 3-fold Logic Unit which is used in both OR mode and AND mode to see coincidence lines. This data is collected in the Trig DAQ.

898 keV signal table

[math]\sigma_Cut[/math]

[math]T_{1/2}[/math] Trig Signal BackG Subtracted Fit Parameters Signal Area Noise Area SNR
0.44 coin Run6980 898 raw.png Run6980 898 sub.png [math]\mu=[/math] 895.744 +/- 5.774e-4 [math]\sigma=[/math] 0.8189 +/- 0.0034 A= 0.0097 +/- 0.0013 B= 4.891e-9 +/- 6.707e-9 C= 2.543e-5 +/- 1.053e-4 0.0217 +/- 6.383e-4 4.643e-4 +/- 5.804e-5 46.678 +/- 0.0124
0.98 sing Run7022 898 raw.png Run7022 898 sub.png [math]\mu=[/math] 897.255 +/- 0.0047 [math]\sigma=[/math] 0.7277 +/- 0.0280 A=0.7027 +/- 0.0129 B= 8.448e-4+/- 4.457e-5 C=-0.7355 +/- 0.0408 1.2938 +/- 0.0381 0.3123 +/- 0.0390 4.143 +/- 0.6977
coin Run7023 898 raw1.png Run7023 898 sub1.png [math]\mu=[/math] 896.818 +/- 0.0075 [math]\sigma=[/math] 0.9856 +/- 0.0276 A= 0.0020 +/- 2.036e-5 B= 1.263e-8 +/- 7.797e-10 C= 1.095e-5 +/- 5.103e-7 0.0049 +/- 1.446e-4 9.518e-5 +/- 1.190e-5 51.591 +/- 0.0036
1.46 sing Run7107 898 raw.png Run7107 898 sub.png [math]\mu=[/math] 897.663 +/- 0.00987 [math]\sigma=[/math] 0.8348 +/- 0.0580 A=0.3925 +/- 0.1107 B=-2.696e-4 +/- 2.725e-7 C= 0.2633 +/- 1.939e-4 1.075 +/- 0.0316 0.0777 +/- 0.0097 13.827 +/- 0.3763
coin Run7108 898 raw.png Run7108 898 sub.png [math]\mu=[/math] 897.780 +/- 0.0025 [math]\sigma=[/math] 0.9737 +/- 0.0186 A= 1.679e-3 +/- 5.996e-7 B= 1.217e-8 +/- 7.211e-11 C= 1.098e-5 +/- 2.962e-8 3.987e-3 +/- 1.174e-4 8.732e-5 +/- 1.092e-5 45.661 +/- 0.0030
2.12 sing Run7203 898 raw.png Run7203 898 sub.png [math]\mu=[/math] 894.701 +/- 0.0127 [math]\sigma=[/math] 0.6371 +/- 0.0569 A=0.3740 +/- 6.200e-5 B= 8.285e-5+/- 4.503e-8 C=-0.0482+/- 5.103e-7 0.6212 +/- 0.0183 0.0723 +/- 0.0090 8.588 +/- 0.3858
coin Run7204 898 raw.png Run7204 898 sub.png [math]\mu=[/math] 890.896 +/- 0.0144 [math]\sigma=[/math] 1.137 +/- 0.0056 A= 7.293e-4 +/- 8.083e-9 B= 8.441e-7 +/- 6.284e-11 C= -7.342e-4 +/- 2.106e-7 0.00199 +/- 5.872e-5 8.296e-5 +/- 1.037e-5 24.032 +/- 0.0015
2.27 sing Run7235 898 raw2.png Run7235 898 sub2.png [math]\mu=[/math] 903.478 +/- 0.0064 [math]\sigma=[/math] 0.7121 +/-0.0877 A=0.2929 +/- 2.373e-4 B= -7.136e-4+/- 1.414e-9 C= 0.6715 +/- 1.777e-4 0.5609+/- 0.0165 0.0862 +/- 0.0108 6.505 +/- 0.3063
coin Run7236 898 raw.png Run7236 898 sub.png [math]\mu=[/math] 905.932 +/- 0.0050 [math]\sigma=[/math] 0.8066 +/- 0.0236 A= 5.888e-4 +/- 2.063e-7 B= 1.238e-6 +/- 4.497e-10 C= -1.106e-3 +/- 4.701e-7 1.170e-3 +/- 3.446e-5 5.310e-5 +/- 6.638e-6 22.033 +/- 8.137e-4


Re-Fit of Run 7203 without Event Cuts

[math]T_{1/2}[/math] Trig Signal BackG Subtracted Fit Parameters Signal Area Noise Area SNR
2.12 sing Run7203 898 raw nocut.png Run7203 898 sub nocut.png [math]\mu=[/math] 894.859 +/- 0.0377 [math]\sigma=[/math] 0.8294 +/- 0.0389 A= 0.1064 +/- 1.281e-4 B=4.131e-4 +/- 3e-9 C= -0.3439 +/- 1.047e-4 0.2214 +/- 0.0065 0.0900 +/- 0.0113 2.459 +/- 0.0082


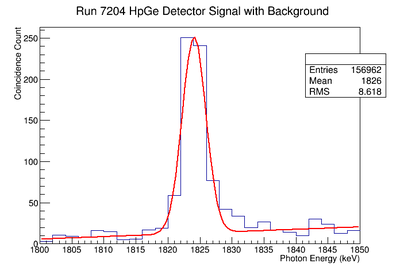
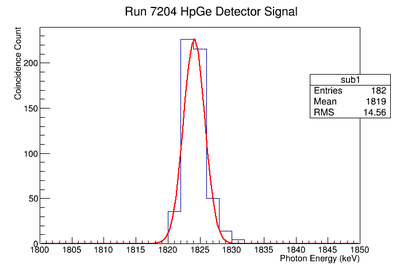
Re-Fit of Run 7203 without Event Cuts and Scaled by 1.66

[math]T_{1/2}[/math] Trig Signal BackG Subtracted Fit Parameters Signal Area Noise Area SNR
2.12 sing Run7203 898 raw ratio3.png Run7203 898 sub ratio3.png [math]\mu=[/math] 894.901 +/- 0.0878 [math]\sigma=[/math] 0.8380 +/- 0.0389 A= 0.1774 +/- 4.505e-4 B=4.931e-5 +/- 9.842e-7 C= -2.231e-3 +/- 9.027e-4 0.3731 +/- 0.0110 0.1532 +/- 0.0192 2.435 +/- 0.1543



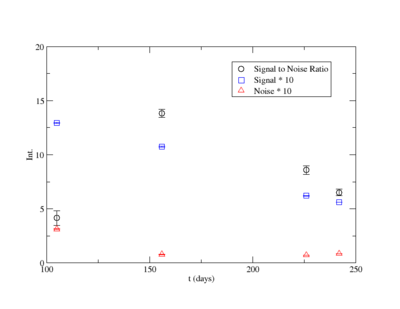
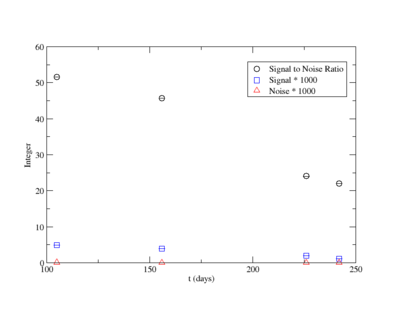
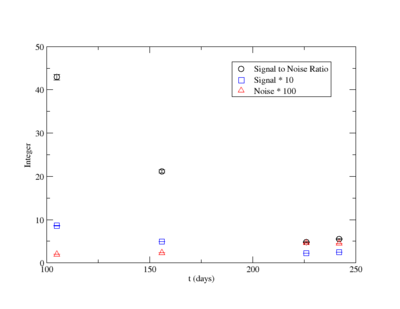
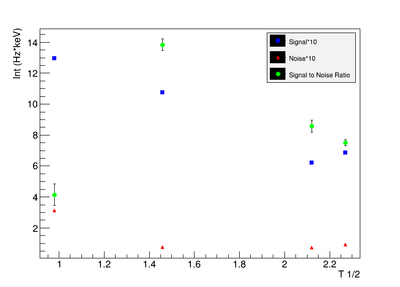
Signal, Noise, and Signal to Noise Ratio plots for 898 keV singles runs.

S N SNR 898 singles2.png SNR 898 singles2.png

Averaging over the last three noise values:

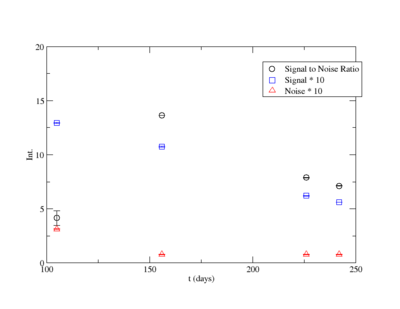
S N SNR 898 singles avg2.png SNR 898 singles avg2.png

Signal, Noise, and Signal to Noise Ratio plots for 898 keV coincidence runs.


S N SNR 898 coin.png SNR 898 coin.png

Averaging over the noise values:

S N SNR 898 coin avg.png SNR 898 coin avg.png

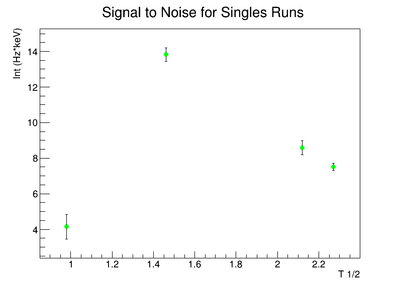
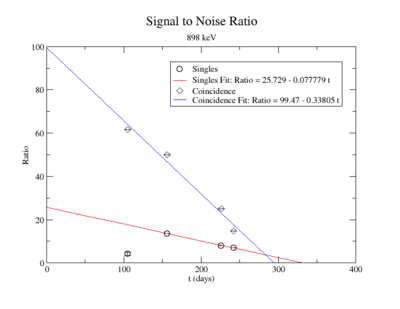
Signal to Noise Ratio (Singles and Coincidence): SNR 898 both.png

SNR 898 both2.png

1836 keV signal table

1836.1 keV Signal Table

[math]T_{1/2}[/math] Trig Signal BackG Subtracted Fit Parameters Signal Area Noise Area SNR
0.44 coin Run6980 1836 raw.png Run6980 1836 sub.png [math]\mu=[/math] 1833.43 +/- 0.0058 [math]\sigma=[/math] 1.447 +/- 0.0228 A= 0.0036 +/- 5.937e-7 B= 1.129e-6 +/- 9.991e-10 C=-2.041e-3 +/- 1.682e-6 0.0127 +/- 3.752e-4 1.937e-4 +/- 2.421e-5 65.781 +/- 0.0096
0.98 sing Run7022 1836 raw1.png Run7022 1836 sub.png [math]\mu=[/math] 1837.7 +/- 0.02 [math]\sigma=[/math] 1.126 +/- 0.0264 A=0.3115 +/- 9.318e-6 B=3.759e-5 +/- 2.793e-7 C=-6.575e-2 +/- 5.102e-4 0.8590 +/- 0.0253 0.0200 +/- 0.0025 42.920 +/- 0.6349
coin Run7023 1836 raw.png Run7023 1836 sub.png [math]\mu=[/math] 1835.86 +/- 0.01 [math]\sigma=[/math] 1.406 +/- 0.0201 A= 0.0018 +/- 2.541e-7 B= 4.930e-9 +/- 5.263e-11 C= 8.945e-6 +/- 8.814e-8 0.0063 +/- 1.853e-4 1.037e-4 +/- 1.297e-5 60.662 +/- 0.0047
1.46 sing Run7107 1836 raw.png Run7107 1836 sub.png [math]\mu=[/math]1838.65 +/- 0.0436 [math]\sigma=[/math] 1.117 +/- 0.0569 A=0.1757 +/- 3.782e-5 B=2.046e-4 +/- 1.5e-9 C=-3.713e-1 +/- 4.940e-5 0.4933 +/- 0.0145 0.0234 +/- 0.0029 21.115 +/- 0.3456
coin Run7108 1836 raw.png Run7108 1836 sub.png [math]\mu=[/math] 1838.003 +/- 0.0115 [math]\sigma=[/math] 1.854 +/- 0.0242 A= 9.717e-4 +/- 4.374e-7 B= 7.051e-7 +/- 1.119e-10 C=-1.291e-3 +/- 1.738e-7 0.0044+/- 1.286e-4 4.248e-5 +/- 5.309e-6 102.838 +/- 0.0033
2.12 sing Run7203 1836 raw.png Run7203 1836 sub.png [math]\mu=[/math] 1831.333 +/- 0.2887 [math]\sigma=[/math] 0.5219 +/- 0.0555 A= 0.1601+/- 1.321e-4 B=-1.429e-6 +/- 1.565e-10 C=2.260e-2 +/- 5.944e-7 0.2214 +/- 0.0065 0.0462 +/- 0.0058 4.796 +/- 0.1192
coin Run7204 1836 raw.png Run7204 1836 sub.png [math]\mu=[/math] 1824.26 +/- 0.0153 [math]\sigma=[/math] 1.570 +/- 0.0871 A= 5.842e-4 +/- 1.552e-5 B= -7.557e-7 +/- 6.718e-11 C= 1.405e-3 +/- 1.754e-7 0.0024 +/- 7.002e-5 1.802e-4 +/- 2.252e-5 13.198 +/- 0.0016
2.27 sing Run7235 1836 raw.png Run7235 1836 sub.png [math]\mu=[/math] 1850.08 +/- 0.0361 [math]\sigma=[/math] 1.238 +/- 0.1486 A=0.0741 +/- 3.058e-4 B=4.389e-4 +/- 5.774e-10 C=-8.040e-1 +/- 1.270e-4 0.2471+/- 0.0073 0.0451 +/- 0.0056 5.478 +/- 0.1354
coin Run7236 1836 raw.png Run7236 1836 sub.png [math]\mu=[/math] 1854.58 +/- 0.1587 [math]\sigma=[/math] 1.696+/- 0.1625 A= 3.873e-4 +/- 8.569e-7 B= -9.482e-7 +/- 7.143e-11 C= 0.0018 +/-3.216e-7 0.0017 +/- 5.083e-5 1.623e-5 +/- 2.028e-6 106.360 +/- 0.0012


Re-Fit of Run 7203 without Event Cuts

[math]T_{1/2}[/math] Trig Signal BackG Subtracted Fit Parameters Signal Area Noise Area SNR
2.12 sing Run7203 1836 raw nocut.png Run7203 1836 sub nocut.png [math]\mu=[/math]1831.55 +/- 1.74 [math]\sigma=[/math]0.6455 +/- 0.0693 A= 0.0658 +/- 0.0007 B= 7.775e-6+/- 1.615e-7 C= -7.311e-3 +/- 2.991e-4 0.1139 +/- 0.0034 0.0216 +/- 0.0027 5.282 +/- 0.0598



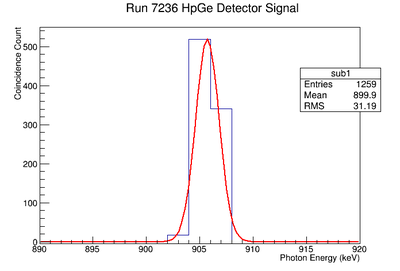
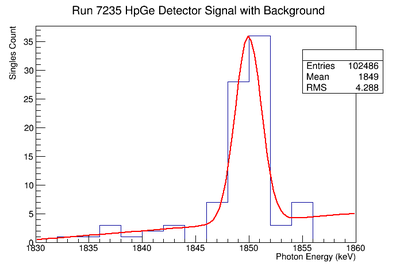
Re-Fit of Run 7236 without Event Cuts

[math]T_{1/2}[/math] Trig Signal BackG Subtracted Fit Parameters Signal Area Noise Area SNR
2.12 sing Run7236 1836 raw nocut.png Run7236 1836 sub nocut.png [math]\mu=[/math] 1860.48 +/- 0.0874 [math]\sigma=[/math]7.160 +/- 0.5751 A= 7.067e-5 +/- 1.151e-6 B= 8.389e-9+/- 1.764e-8 C= -1.293e-5 +/- 3.280e-5 0.0013 +/- 3.914e-5 0.0021 +/- 0.0003 0.6289 +/- 0.0007


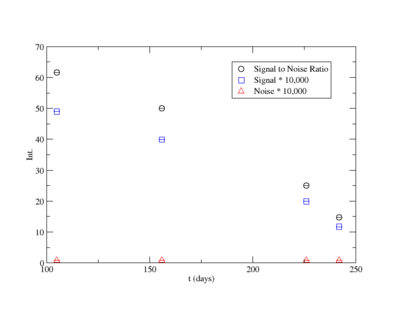
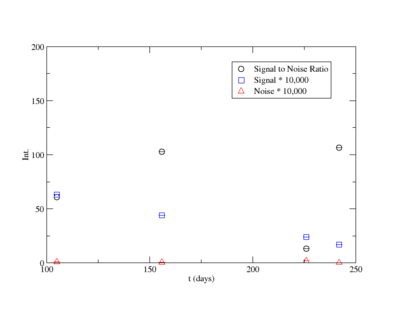
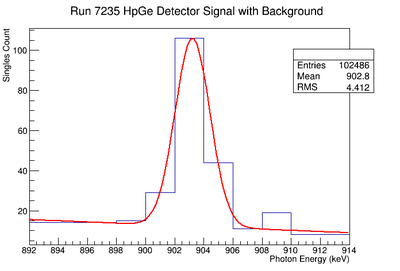
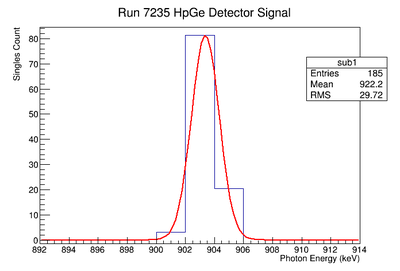
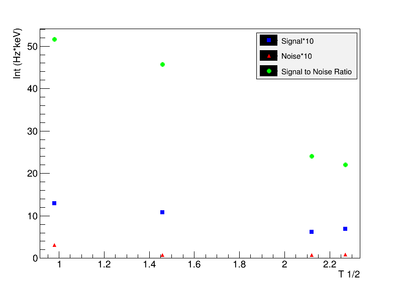
Signal, Noise, and Signal to Noise Ratio plots for 1836 keV singles runs.

S N SNR 1836 singles.png SNR 1836 singles.png

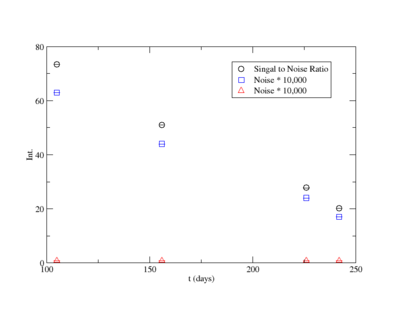
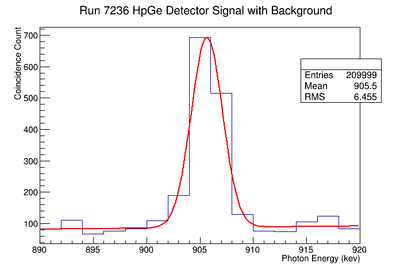
Signal, Noise, and Signal to Noise Ratio plots for 1836 keV coincidence runs.

S N SNR 1836 coin.png SNR 1836 coin.png

Averaging over the noise values:

S N SNR 1836 coin avg.png SNR 1836 coin avg.png

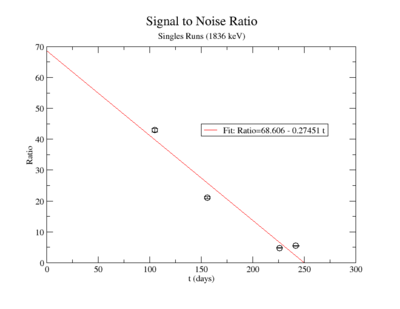
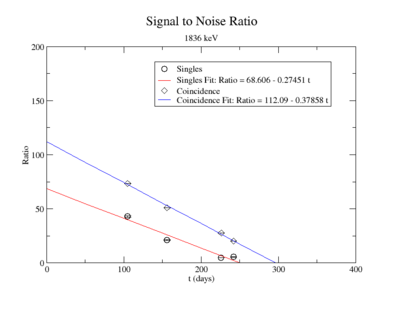
Signal to Noise Ratio (Singles and Coincidence): SNR 1836 both.png



Error analysis

Half-life

Values

898 keV Singles

Days [math]T_{1/2}[/math] Trig Energy Window Energy Calibration Linear Fit of Background Gaussian Integration of Signal Total Systematic Error
105 0.98 sing [math] {+0.005} \atop { -0.009}[/math] [math] {+0.014} \atop { -0.025}[/math] [math]\pm 0.0025[/math] [math]\pm 0.07[/math] [math] {+0.073} \atop { -0.078}[/math]
156 1.46 sing [math] {+0.0062} \atop { -0.032}[/math] [math] {+0.0071} \atop { -0.0212}[/math] [math] {+0.0065} \atop { -0.0063}[/math] [math]\pm 0.0547[/math] [math] {+0.057} \atop { -0.077}[/math]
226 2.12 sing [math] {+0.1554} \atop { -0.1128}[/math] [math] {+0.0562} \atop { -0.0774}[/math] [math] {+0.0128} \atop { -0.0122}[/math] [math]\pm 0.0174[/math] [math] {+0.213} \atop { -0.191}[/math]
242 2.27 sing [math] {+0.0069} \atop { -0.0481}[/math] [math] {+0.0246} \atop { -0.0697}[/math] [math]\pm 0.01[/math] [math]\pm 0.062[/math] [math] {+0.07} \atop { -0.133}[/math]

898 keV Coincidence

Days [math]T_{1/2}[/math] Trig Energy Window Energy Calibration Linear Fit of Background Gaussian Integration of Signal Coincidence Energy Total Systematic Error
105 0.98 coin [math] {+2.9e-5} \atop { -2.1e-5}[/math] [math] \pm 1.6e-5[/math] [math] {+7.358e-6} \atop { -7.092e-6}[/math] [math]\pm 0.00018[/math] [math] {+5.68e-4} \atop { -1.75e-3}[/math] [math] {+6.39e-4} \atop { -1.8e-3}[/math]
156 1.46 coin [math] {+1.7e-5} \atop { -2.0e-6}[/math] [math] \pm 1.6e-5[/math] [math] {+2.004e-6} \atop { -1.990e-6}[/math] [math] {+7.611e-5} \atop { -7.605e-5}[/math] [math] {+4.03e-4} \atop { -6.22e-4}[/math] [math] {+4.43e-4} \atop { -6.45e-4}[/math]
226 2.21 coin [math] {+2.0e-5} \atop { -1.06e-4}[/math] [math] {+3.5e-5} \atop { -6.8e-5}[/math] [math] {+8.041e-6} \atop { -7.859e-6}[/math] [math]\pm 0.00013[/math] [math] {+4.92e-4} \atop { -1.06e-3}[/math] [math] {+5.62e-4} \atop { -1.24e-3}[/math]
242 2.27 coin [math] {+3.0e-6} \atop { -1.0e-6}[/math] [math] {+2.0e-6} \atop { -8e-6}[/math] [math] {+4.436e-6} \atop { -4.365e-6}[/math] [math]\pm 1.078e-5[/math] [math] {+3.63e-4} \atop { -1.52e-3}[/math] [math] {+3.68e-4} \atop { -1.53e-3}[/math]


1836.1 keV Singles

Days [math]T_{1/2}[/math] Trig Energy Window Energy Calibration Linear Fit of Background Gaussian Integration of Signal Total Systematic Error
105 0.98 sing [math] {+0.001} \atop { -8.0e-4}[/math] [math]\pm 0.0028[/math] [math] {+0.0051} \atop { -0.0049}[/math] [math]\pm 0.0197[/math] [math]\pm 0.021[/math]
156 1.46 sing [math] {+0.001} \atop { -0.004}[/math] [math] {+0.0141} \atop { -0.0071}[/math] [math]\pm 0.0014[/math] [math]\pm 0.0240[/math] [math] {+0.028} \atop { -0.026}[/math]
226 2.12 sing [math] {+0.0288} \atop { -0.0211}[/math] [math] {+0.0122} \atop { -0.0244}[/math] [math] {+0.0092} \atop { -0.0085}[/math] [math] {+0.0321} \atop { -0.0320}[/math] [math] {+0.053} \atop { -0.056}[/math]
242 2.27 sing [math] {+6.0e-4} \atop { -0.013}[/math] [math]\pm 0.0041[/math] [math] {+0.0055} \atop { -0.0054}[/math] [math] {+0.027} \atop { -0.0272}[/math] [math] {+0.028} \atop { -0.033}[/math]


1836.1 keV Coincidence

Days [math]T_{1/2}[/math] Trig Energy Window Energy Calibration Linear Fit of Background Gaussian Integration of Signal Coincidence Energy Cut Total Systematic Error
105 0.98 coin [math] {+3.8e-5} \atop { -3.4e-5}[/math] [math] {+3.2e-5} \atop { -3.1e-5}[/math] [math] {+2.505e-6} \atop { -2.475e-6}[/math] [math]\pm 8.97e-5[/math] [math] {+3.11e-4} \atop { -2.57e-3}[/math] [math] {+3.91e-4} \atop { -2.64e-3}[/math]
156 1.46 coin [math] {+2.0e-5} \atop { -9.0e-6}[/math] [math] {+1.2e-5} \atop { -3.7e-5}[/math] [math] {+3.422e-6} \atop { -3.347e-6 }[/math] [math]\pm 5.83e-5[/math] [math] {+4.63e-4} \atop { -2.82e-3}[/math] [math] {+4.98e-4} \atop { -2.87e-3}[/math]
226 2.12 coin [math] {+3.9e-5} \atop { -1.58e-4}[/math] [math] {+6.9e-5} \atop { -13.6e-5}[/math] [math] {+1.515e-5} \atop { -1.481e-5}[/math] [math]\pm 2.13e-4[/math] [math] {+1.16e-3} \atop { -5.77e-3}[/math] [math] {+1.29e-3} \atop { -6.07e-3}[/math]
242 2.27 coin [math] {+2.0e-6} \atop { -7.0e-6}[/math] [math] \pm 3.0e-6[/math] [math]\pm 6.18e-6[/math] [math]\pm 0.00012 [/math] [math] {+4.51e-4} \atop { -1.21e-3}[/math] [math] {4.72e-4} \atop { -1.23e-3}[/math]

Percent Error

898 keV Singles

Days [math]T_{1/2}[/math] Trig Energy Window Energy Calibration Linear Fit of Background Gaussian Integration of Signal Total Systematic Error
105 0.98 sing [math] {+0.367%} \atop { -0.660%}[/math] [math] {+1.026%} \atop { -1.83%}[/math] [math]\pm 0.183%[/math] [math]\pm 5.132%[/math] [math] {+5.32%} \atop { -5.71%}[/math]
156 1.46 sing [math] {+0.713%} \atop { -3.68%}[/math] [math] {+0.816%} \atop { -2.438%}[/math] [math] {+0.747%} \atop { -0.724%}[/math] [math]\pm 6.29%[/math] [math] {+6.52%} \atop { -8.80%}[/math]
226 2.12 sing [math] {+32.83%} \atop { -23.83%}[/math] [math] {+11.87%} \atop { -16.35%}[/math] [math] {+2.7%} \atop { -2.58%}[/math] [math]\pm 3.68%[/math] [math] {+44.94%} \atop { -40.44%}[/math]
242 2.27 sing [math] {+1.19%} \atop { -8.28%}[/math] [math] {+4.24%} \atop { -12.0%}[/math] [math]\pm 1.72%[/math] [math]\pm 10.68%[/math] [math] {+12.1%} \atop { -22.99%}[/math]


898 keV Coincidence

Days [math]T_{1/2}[/math] Trig Energy Window Energy Calibration Linear Fit of Background Gaussian Integration of Signal Coincidence Energy Total Systematic Error
105 0.98 coin [math] {+0.56%} \atop { -0.404%}[/math] [math] {+0.31%} \atop { -1.21%}[/math] [math] {+0.142%} \atop { -0.136%}[/math] [math]\pm 3.46%[/math] [math] {+10.92%} \atop { -33.65%}[/math] [math] {+12.29%} \atop { -35.44%}[/math]
156 1.46 coin [math] {+0.405%} \atop { -0.048%}[/math] [math] {+0.36%} \atop { -0.31%}[/math] [math] {+0.048%} \atop { -0.047%}[/math] [math]\pm 1.81%[/math] [math] {+9.6%} \atop { -14.8%}[/math] [math] {+10.51%} \atop { -12.27%}[/math]
226 2.21 coin [math] {+0.588%} \atop { -3.12%}[/math] [math] {+0.59%} \atop { -1.74%}[/math] [math] {+0.237%} \atop { -0.231%}[/math] [math]\pm 3.82%[/math] [math] {+14.5%} \atop { -31.2%}[/math] [math] {+16.11%} \atop { -36.23%}[/math]
242 2.27 coin [math] {+0.2%} \atop { -0.067%}[/math] [math] {+0.13%} \atop { -0.267%}[/math] [math] {+0.296%} \atop { -0.291%}[/math] [math]\pm 0.719%[/math] [math] {+24.2%} \atop { -101.3%}[/math] [math] {+24.55%} \atop { -101.67%}[/math]


1836.1 keV Singles

Days [math]T_{1/2}[/math] Trig Energy Window Energy Calibration Linear Fit of Background Gaussian Integration of Signal Total Systematic Error
105 0.98 sing [math] {+0.119%} \atop { -0.095%}[/math] [math]\pm 0.33%[/math] [math] {+0.606%} \atop { -0.582%}[/math] [math]\pm 2.34%[/math] [math] {+2.46%} \atop { -2.45%}[/math]
156 1.46 sing [math] {+0.199%} \atop { -0.798%}[/math] [math] {+2.81%} \atop { -1.42%}[/math] [math]\pm 0.279%[/math] [math]\pm 4.79%[/math] [math] {+5.66%} \atop { -5.28%}[/math]
226 2.12 sing [math] {+10.21%} \atop { -7.48%}[/math] [math] {+4.32%} \atop { -8.65%}[/math] [math] {+3.26%} \atop { -3.01%}[/math] [math] {+11.37%} \atop { -11.34%}[/math] [math] {+18.74%} \atop { -19.94%}[/math]
242 2.27 sing [math] {+0.245%} \atop { -5.31%}[/math] [math]\pm 1.674%[/math] [math] {+2.246%} \atop { -2.205%}[/math] [math] {+11.025%} \atop { -11.107%}[/math] [math] {+11.414%} \atop { -13.303%}[/math]


1836.1 keV Coincidence

Days [math]T_{1/2}[/math] Trig Energy Window Energy Calibration Linear Fit of Background Gaussian Integration of Signal Coincidence Energy Cut Total Systematic Error
105 0.98 coin [math] {+0.613%} \atop { -0.55%}[/math] [math] {+1.27%} \atop { -0.5%}[/math] [math]\pm 0.04%[/math] [math]\pm 1.45%[/math] [math] {+5.02%} \atop { -41.45%}[/math] [math] {+7.05%} \atop { -42.52%}[/math]
156 1.46 coin [math] {+0.435%} \atop { -0.196%}[/math] [math] {+0.522%} \atop { -0.804%}[/math] [math] {+0.074%} \atop { -0.073% }[/math] [math]\pm 1.267%[/math] [math] {+10.07%} \atop { -61.3%}[/math] [math] {+11.09%} \atop { -62.31%}[/math]
226 2.12 coin [math] {+0.629%} \atop { -2.55%}[/math] [math] {+1.11%} \atop { -1.10%}[/math] [math] {+0.244%} \atop { -0.239%}[/math] [math]\pm 3.44%[/math] [math] {+18.71%} \atop { -93.06%}[/math] [math] {+20.74%} \atop { -96.77%}[/math]
242 2.27 coin [math] {+0.125%} \atop { -0.438%}[/math] [math] {+0.125%} \atop { -0.188%}[/math] [math]\pm 0.386% [/math] [math]\pm 7.5% [/math] [math] {+28.2%} \atop { -75.6%}[/math] [math] {29.41%} \atop { -76.62%}[/math]

SNR

The signal to noise ratio is

Days [math]T_{1/2}[/math] Trig SNR Statistical Error Systematic Error
105 0.98 sing 42.07 [math]\pm 0.0483[/math] [math]\pm 0.0197[/math]
coin 9.65 [math]\pm 1.04e-3 [/math] [math] {+1.47e-4} \atop { -1.11e-4}[/math]
156 1.46 sing 21.52 [math]\pm 0.0420 [/math] [math] {+0.028} \atop { -0.026}[/math]
coin 7.16 [math]\pm 1.02e-3 [/math] [math] {+7.31e-5} \atop { -7.43e-5}[/math]
226 2.12 sing 4.64 [math]\pm 0.0597 [/math] [math] {+0.053} \atop { -0.056}[/math]
coin 9.65 [math]\pm 1.09e-3 [/math] [math] {+2.39e-4} \atop { -3.11e-4}[/math]
242 2.27 sing 5.43 [math]\pm 0.0325 [/math] [math] {+0.028} \atop { -0.033}[/math]
coin 2.49 [math]\pm 9.89e-4 [/math] [math] {+1.20e-4} \atop { -1.21e-4}[/math]

=other

Energy Trig [math]T_{1/2}[/math] (days) [math]N_0[/math] (before efficiency) [math]N_0[/math] (after efficiency) [math]T_{final}[/math] [math] N(t_{final})[/math] [math]\frac{N(t_{final})}{N_0}[/math]
898 sing 130.39 +/- 26.26 1.281e-8 +/- 2.236e-9 1.636e-6 +/- 2.957e-7 383.63 [math] {+202.83} \atop { -119.44}[/math] 1.351e-7 +/- 7.551e-8 0.0826 +/- 0.0485
coin 108.18 +/- 4.89 6.411e-11 +/- 1.314e-12 3.794e-8 +/- 2.633e-9 483.60 [math] {+111.97} \atop { -83.40}[/math] 1.636e-9 +/- 3.954e-10 0.0431 +/- 0.0108
1836.1 sing 106.16 +/- 8.63 9.634e-9 +/- 1.089e-9 3.089e-6 +/- 3.619e-7 264.94 [math] {+29.37} \atop { -26.24}[/math] 5.519e-7 +/- 8.705e-8 0.1787 +/- 0.0351
coin 100.10 +/- 4.0 8.147e-11 +/- 1.670e-12 4.171e-8 +/- 1.860e-9 305.63 [math] {+64.72} \atop { -49.63}[/math] 5.721e-9 +/- 1.238e-9 0.1371 +/- 0.0303

Run7204 Y88 898 signalnoise.png Run7204 Y88 898 signal.png

Run7235 Y88 898 signalnoise.png Run7235 Y88 898 signal.png

Run7236 Y88 898 signalnoise.png Run7236 Y88 898 signal.png

898 keV Signal and Background Noise Table

Run # Area of Signal Area of Background Signal to Noise Ratio
7203 130.17 120.59 1.08
7204 825.34 558.66 1.48
7235 194.38 60.23 3.23
7236 1429.75 436.93 3.27

A_W_thesis

Run7204 Y88 1836 signalnoise.png Run7204 Y88 1836 signal.png

Run7235 Y88 1836 signalnoise.png Run7235 Y88 1836 signal.png

Run7236 Y88 1836 signalnoise.png Run7236 Y88 1836 signal.png

1836.1 keV Signal and Background Noise Table

Run # Area of Signal Area of Background Signal to Noise Ratio
7203 83.29 24.73 3.37
7204 944.58 101.68 9.29
7235 82.25 20.90 3.94
7236 1849.86 97.64 18.95


HpGe Detector

Run Source Energy Expected rate (Hz) HpGe Det B Rate (ADC 7) (Hz) HpGe Eff (%)
7027 Na-22 511 1589.218 +/- 49.425 18.07 +/- 0.111 1.137 +/- 0.0317
7025 Cs-137 661.657 2548.03 +/- 80.008 25.468+/- 0.172 0.9995 +/- 0.0321
7029 Mn-54 834.848 41.405 +/- 1.300 0.485 +/- 0.014 1.171 +/- 0.0427
7026 Co-60 1173.228 1876.619 +/- 58.926 11.03 +/- 0.106 0.588 +/- 0.0328
7027 Na-22 1274.537 888.264 +/- 27.625 4.857 +/- 0.034 0.5468 +/- 0.0319
7026 Co-60 1332.492 1878.167 +/- 58.974 9.584 +/- 0.023 0.510 +/- 0.0315


SingEff corrected.png


Extrapolated Efficiency

Source Energy HpGe Eff (%)
Y-88 898 1.036 +/- 0.0226
Y-88 1836.1 0.1983 +/- 0.0178


Exp Fit including Cs-137
  1  Constant     7.96246e-01   6.78458e-02   6.83891e-05  -2.33206e-03
  2  Slope       -1.07699e-03   7.10063e-05   7.15739e-08  -2.09517e+00

f(x) = exp(p0+p1*x).

Extrapolated Efficiency

Source Energy HpGe Eff (%)
Y-88 898 0.8429 +/- 0.0034
Y-88 1836.1 0.3069 +/- 0.0192


SingEff ExpoFit.png


Energy Trig [math]N_0[/math] (before efficiency)
898 sing 1.281e-8 +/- 2.254e-9
coin 6.411e-11 +/- 3.572e-12
1836.1 sing 9.634e-9 +/- 1.102e-9
coin 8.147e-11 +/- 2.987e-12
Exp Fit including all Na-22 points and excluding Mn-54
  1  Constant     6.36491e-01   4.70444e-02   1.00271e-05  -3.28621e-03
  2  Slope       -9.81232e-04   5.68236e-05   1.21109e-08  -1.59453e+00


Extrapolated Efficiency

Source Energy HpGe Eff (%)
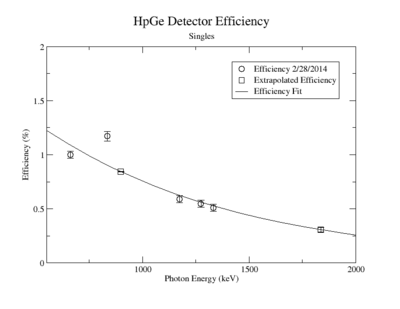
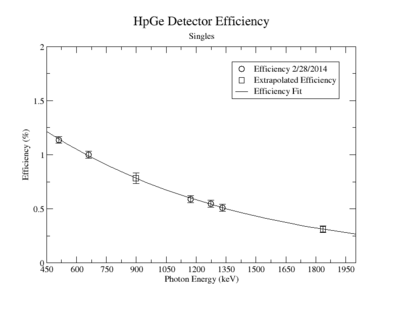
Y-88 898 0.7830 +/- 0.0471
Y-88 1836.1 0.3119 +/- 0.0310


SingEff NoMn.png

Energy Trig [math]N_0[/math] (before efficiency)
898 sing 1.281e-8 +/- 2.254e-9
coin 6.411e-11 +/- 3.572e-12
1836.1 sing 9.634e-9 +/- 1.102e-9
coin 8.147e-11 +/- 2.987e-12

Efficiency on 2/28/2014

Run Source Energy Expected rate (Hz) HpGe Det B Rate (ADC 7) (Hz) HpGe Eff (%)
7028 Ba-133 80.9971 1067.468 +/- 1.131 14.483 +/- 1.442 1.357
7028 Ba-133 276.3997 221.297 +/- 0.2345 4.239 +/- 0.9671 1.916
7028 Ba-133 302.8510 574.310 +/- 0.6085 9.523 +/- 0.5539 1.658
7028 Ba-133 356.0134 1941.418 +/- 2.057 27.130 +/- 1.316 1.397
7028 Ba-133 383.8480 278.416 +/- 0.2950 3.982 +/- 0.2440 1.430
7027 Na-22 511 1589.218 +/- 1.842 17.545 +/- 0.4560 1.104
7025 Cs-137 661.657 2548.022 +/- 2.222 25.622+/- 0.3286 1.006
7029 Mn-54 834.848 4032.782 +/- 0.0114 0.2911 +/- 0.1667 0.0072
7026 Co-60 1173.228 1876.619 +/- 0.2687 11.062 +/- 0.1215 0.589
7027 Na-22 1274.537 888.264 +/- 1.029 4.685 +/- 0.0825 0.527
7026 Co-60 1332.492 1878.167 +/- 0.2690 9.616 +/- 0.1181 0.512

HpGeEffPlot 2 28.pngHpGeEffPlot 2 28 2014.png

HpGeEffPlot 7 11.png

Run Source Energy Expected rate (Hz) NaI Det B Rate (ADC 7) (Hz) NaI Eff (%)
7027 Na-22 511 1589.218 +/- 49.425 14.86 +/- 0.0945 0.9351 +/- 0.0317
7025 Cs-137 661.657 2548.03 +/- 80.008 23.45 +/- 0.9729 0.9203 +/- 0.0520
7026 Co-60 1173.228 1876.619 +/- 58.926 8.001 +/- 0.0953 0.4264 +/- 0.0336
7027 Na-22 1274.537 888.264 +/- 27.625 4.05 +/- 0.0247 0.4559 +/- 0.0317
7026 Co-60 1332.492 1878.167 +/- 58.974 7.234 +/- 0.1675 0.3852 +/- 0.0390

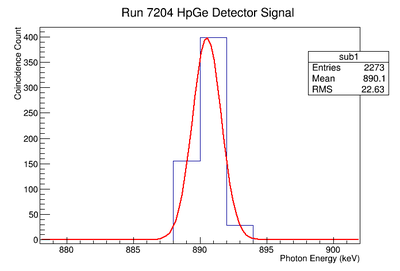
Signal, Noise, and Signal to Noise Ratio plots for 898 keV singles runs.

SNR 898 singles plot.png Ratio 898 singles plot.png

Signal, Noise, and Signal to Noise Ratio plots for 898 keV coincidence runs.

SNR 898 coin plot.png Ratio 898 coin plot.png

Signal Diagram.png Signal Diagram 2.png


[math]\sigma_Fit[/math]

[math]T_{1/2}[/math] Trig Fit Parameters Signal Area Noise Area SNR
0.98 sing [math]\mu=[/math] 897.260 +/- 0.0047 [math]\sigma=[/math] 0.7074 +/- 0.0280 A=0.725 +/- 0.0129 B= 8.448e-4+/- 4.457e-5 C=-0.7355 +/- 0.0408 0.9938 +/- 0.0054 0.3039 +/- 0.0380 3.270 +/- 0.0243
coin [math]\mu=[/math] +/- [math]\sigma=[/math] +/- A= +/- B= +/- C= +/- +/- +/- +/-
2.27 sing [math]\mu=[/math] 903.482 +/- 0.0064 [math]\sigma=[/math] 0.6595 +/- 0.0877 A= 0.3199 +/- 0.0156 B= -7.248e-4+/- 9.968e-7 C= 6.816e-1 +/- 8.138e-4 0.5146 +/- 0.0073 0.0852 +/- 0.0107 6.037 +/- 0.0082
coin [math]\mu=[/math] +/- [math]\sigma=[/math] +/- A= +/- B= +/- C= +/- +/- +/- +/-

Fit method

Do the fit:

get parameters for line

Then fill 1 histogram with line

Then subtract 


TH1F *coin1=new TH1F("coin1","coin1",30,1800,1860);

ntuple->Draw("ADC7*0.604963-49.7001 >>coin1")

TH1F *lin1=new TH1F("lin1","line1",30,1800,1860);

for(int i=1800;i<1861;i++){
lin1->Fill(i,-2028+1.12*i)
}

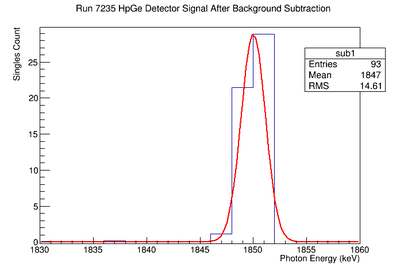
TH1F *sub1=new TH1F("sub1","sub1",30,1800,1860);

sub1->Add(coin1,1);
sub1->Add(lin1,-1);

sub1->Draw();


A pdf of the Mathematica notebook used to calculate background area, gaussian area, and plot signal/noise vs. activity.

File:AW Background Noise custom4.pdf

All the ROOT fit parameters used to find the background and the resulting peaks.

File:Y-88 Fit Log Scaled&Cut.pdf

Integrating the gaussian of the HpGe detector signal.

File:AW Gaussian Integral2.pdf



[math] f(x)=A \textstyle \int_{\mu-2\sigma}^{\mu+2\sigma} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2} \operatorname{d}\!x +B x +C[/math]


Old Analysis Section

Run6980_Y88

Run7023_Y88

Run7108_Y88

Run7161_Y88

Run7204_Y88

Run7236_Y88



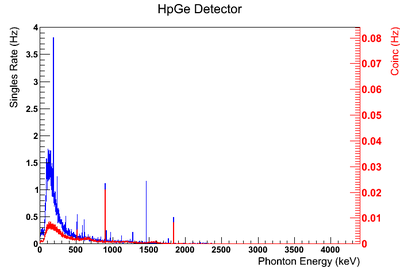
Run7023 Y88 scaled.png Run7023 OverlayCoin Cuts.png

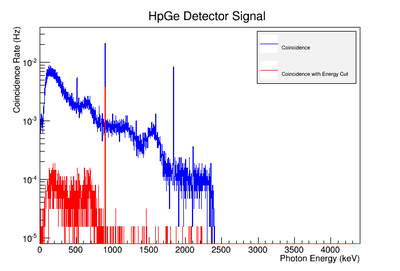
Run7023 OverlayCoin Cuts log.png

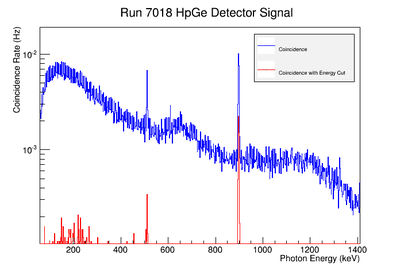
Using our Y-88 source, our set-up allows us to perform runs with the detectors in coincidence (AND mode) or singles (OR mode). The figure on the left shows the HpGe detector's coincidence events (red) that occurred within a 200 ns timing window. This graph has been overlaid with the same detector’s single events (blue). We can see that by having the detectors in coincidence, the noise is reduced and several peaks, which do not have multiple photons in coincidence, are removed.

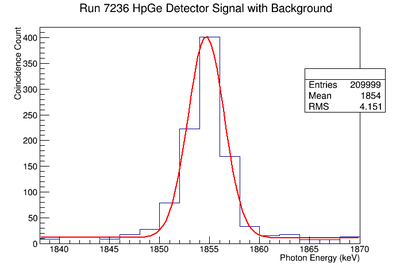
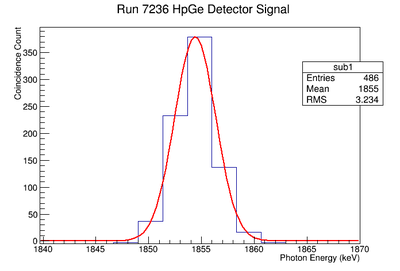
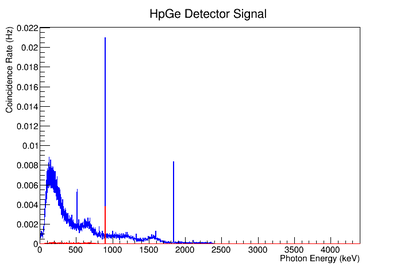
The coincidence run does not show the two energy peaks associated with Y-88 decay alone. Even though we require coincidence for the system to trigger, there is still noise. These peaks could be Compton events contaminating the coincidence and accidentals. Photons can loss a portion of their energy traveling to the detector. They do not necessarily have to deposit all of their energy into the detector either. The photon can Compton scatter out. It is not possible to tell the difference between a photon that deposited all of its energy from a scattered photon, since the speed of light is so fast and the resolution of the detector so poor. The photons can, however, be distinguished if an energy cut is applied. In order to remove the Compton events and the accidentals, we can require the photon energy to be completely deposited into the detector. This can be achieved by placing an energy cut on the NaI detector around the high energy Y-88 peak. This will remove other unwanted photon energies. The graph on the right is an overlay of the coincidence signal before (blue) and after (red) an energy cut is applied to the companion detector (NaI detector). The noise seen at low energies is greatly reduced after including the cut and improved the signal.



Background subtraction

898 keV analysis

The raw Histograms and fits may be found here A_W_thesis_old#898_keV_signal_table

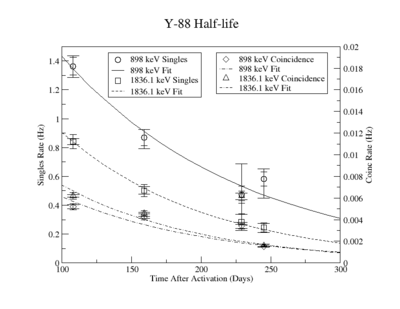
The Measured half life is

Y-88 Half-life

Days [math]T_{1/2}[/math] Trig Integral Statistical Error Systematic Error Systematic Error without Coincidence Energy Cut
108 1.01 sing 1.364 [math]\pm 0.062 [/math] [math] {+0.073} \atop { -0.078}[/math] N/A
coin 0.0052 [math]\pm 2.864e-4 [/math] [math] {+6.39e-4} \atop { -1.8e-3}[/math] [math] {+1.86e-4} \atop { -1.84e-4}[/math]
159 1.49 sing 0.8697 [math]\pm 0.055 [/math] [math] {+0.057} \atop { -0.077}[/math] N/A
coin 0.0042 [math]\pm 2.263e-4 [/math] [math] {+4.43e-4} \atop { -6.45e-4}[/math] [math] {+8.3e-5} \atop { -7.82e-5}[/math]
229 2.15 sing 0.4733 [math]\pm 0.058 [/math] [math] {+0.213} \atop { -0.191}[/math] N/A
coin 0.0034 [math]\pm 2.587e-4 [/math] [math] {+5.62e-4} \atop { -1.24e-3}[/math] [math] {+1.41e-4} \atop { -2.17e-4}[/math]
245 2.30 sing 0.5807 [math]\pm 0.049 [/math] [math] {+0.07} \atop { -0.133}[/math] N/A
coin 0.0015 [math]\pm 5.454e-5 [/math] [math] {+3.68e-4} \atop { -1.53e-3}[/math] [math] {+1.27e-5} \atop { -1.47-5}[/math]



Y-88 Halflife Update.png



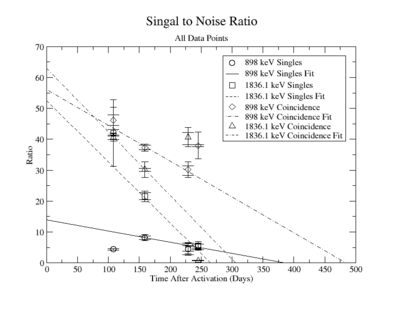
The signal to noise ratio is

Days [math]T_{1/2}[/math] Trig SNR Statistical Error Systematic Error
108 1.01 sing 4.368 [math]\pm 0.252 (5.77%) [/math] [math] {+0.232} \atop { -0.249}[/math]
coin 46.181 [math]\pm 4.204 (9.10%)[/math] [math] {+1.653} \atop { -1.635}[/math]
159 1.49 sing 8.228 [math]\pm 0.999 (12.14%)[/math] [math] {+0.536} \atop { -0.724}[/math]
coin 37.30 [math]\pm 1.132 (3.03%)[/math] [math] {+0.739} \atop { -0.694}[/math]
229 2.15 sing 4.478 [math]\pm 2.047 (45.71%) [/math] [math] {+2.008} \atop { -1.811}[/math]
coin 30.195 [math]\pm 2.480 (8.21%)[/math] [math] {+1.253} \atop { -1.926}[/math]
245 2.30 sing 5.494 [math]\pm 1.415 (25.75%)[/math] [math] {+0.665} \atop { -1.263}[/math]
coin 37.994 [math]\pm 4.287 (11.28%)[/math] [math] {+0.322} \atop { -0.372}[/math]

The first data point for the singles 898 keV was not included in the signal to noise fit. At the time of measurement, the noise was larger. This could be from contaminates with short half-lives in the sample that decayed away. Only elements with longer half-lives, such as Y-88, remained. The background of the remaining three data points were averaged.

For the 898 keV coincidence signal to noise fit, the last data point was not included. The length of the run and activities in the room, such as the nitrogen tank refilling, during counting caused the peak to be spread over a larger energy range. This also meant that the background noise would be larger. The background of the first three data points were averaged. 

what about third data point

SNR BW Update.png


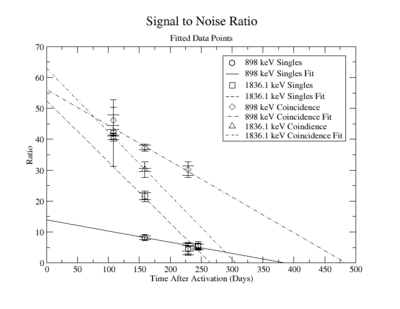
The following plot is the signal to noise ratio with only the data points used to obtain a fit.


SNR BW2 Update.png



Energy Trig [math]T_{1/2}[/math] (days) [math]A_0[/math] (before efficiency) (Hz) [math]N_0[/math] (before efficiency) (nuclei) [math]A_0[/math] (after efficiency) (Hz) [math]N_0[/math] (after efficiency) (nuclei) [math]T_{final}[/math] (days) [math]A(t_{final})[/math] (Hz) [math] N(t_{final})[/math] (nuclei) [math]\frac{N(t_{final})}{N_0}[/math]
898 sing 130.39 +/- 26.26 115.05 +/- 27.87 3.081 +/- 0.538 3.464 +/- 0.604 4.096e7 +/- 7.147e6 4.604e7 +/- 8.034e6 393.544 +/- 71.131 422.377 +/- 79.957 5.231e9 +/- 9.454e8 5.88e9 +/-1.063e9 383.63 [math] {+202.83} \atop { -119.44}[/math] 32.506 +/- 18.162 36.539 +/- 20.416 4.320e8 +/- 2.414e8 4.857e8 +/- 2.714e8 0.0826 +/- 0.0485
coin 108.18 +/- 4.89 0.0154 +/- 0.0003 204958.085 +/- 4201.641 9.125 +/- 0.633 1.213e8 +/- 8.416e6 483.60 [math] {+111.97} \atop { -83.40}[/math] 0.3935 +/- 0.0951 5.230e6 +/- 1.264e6 0.0431 +/- 0.0108
1836.1 sing 106.16 +/- 8.63 2.317 +/- 0.262 3.080e7 +/- 3.480e6 742.929 +/- 87.053 9.874e9 +/- 1.157e9 264.94 [math] {+29.37} \atop { -26.24}[/math] 132.74 +/- 20.938 1.764e9 +/- 2.783e8 0.1787 +/- 0.0351
coin 100.10 +/- 4.0 0.0196 +/- 0.0004 260440.778 +/- 5339.036 10.033 +/- 0.447 1.334e8 +/- 5.946e6 305.63 [math] {+64.72} \atop { -49.63}[/math] 1.376 +/- 0.298 1.829e7 +/- 3.958e6 0.1371 +/- 0.0303


March 2015

Energy Trig [math]T_{1/2}[/math] (days) [math]A_0[/math] (before efficiency) (Hz) [math]N_0[/math] (before efficiency) (nuclei) [math]A_0[/math] (after efficiency) (Hz) [math]N_0[/math] (after efficiency) (nuclei) [math]T_{final}[/math] (days) [math]A(t_{final})[/math] (Hz) [math] N(t_{final})[/math] (nuclei) [math]\frac{N(t_{final})}{N_0}[/math]
898 sing 152.83 +/- 26.99 1.371 +/- 0.239 1.822e7 +/- 3.180e6 175.093 +/- 31.647 2.327e9 +/- 4.206e8 4.057e9 +/- 7.333e8 [math] {+} \atop { -}[/math]
coin 108.18 +/- 4.89 0.0154 +/- 0.0003 204958.085 +/- 4201.641 9.125 +/- 0.633 1.213e8 +/- 8.416e6 483.60 [math] {+111.97} \atop { -83.40}[/math] 0.3935 +/- 0.0951 5.230e6 +/- 1.264e6 0.0431 +/- 0.0108
1836.1 sing 101.099 +/- 14.473 0.904 +/- 0.102 1.202e7 +/- 1.358e6 289.993 +/- 33.98 3.854e9 +/- 4.516e8 5.471e9 +/- 6.410e8 [math] {+} \atop { -}[/math]
coin 100.10 +/- 4.0 0.0196 +/- 0.0004 260440.778 +/- 5339.036 10.033 +/- 0.447 1.334e8 +/- 5.946e6 305.63 [math] {+64.72} \atop { -49.63}[/math] 1.376 +/- 0.298 1.829e7 +/- 3.958e6 0.1371 +/- 0.0303


Average [math] N_0[/math]: [math](38.4 \pm 5.29) \times 10^{8}[/math]


[math]N = \frac{A}{\sigma \Phi \left ( 1 - e^{- \lambda t_i} \right ) e^{- \lambda t_d}}[/math]


[math]N[/math] = number of atoms in sample that were activated
[math]A[/math]= activity measure at time [math]t_d[/math]
[math]\sigma[/math] = photo nuclear cross section
[math]\Phi[/math] = photon flux
[math]\lambda[/math] = decay constant
[math]t_i[/math] = irradiation time
[math]t_d[/math] = decay time that has expired until A is measured

Using nickel target you can take ratios to try and approximate [math]\Phi[/math]

Media:ContHealtPhys_Bevelacqua_2004APPIII.pdf


http://www.nist.gov/pml/data/xcom/


Sample [math]E_{\gamma}[/math] (keV) Activity (Hz) Parent Nuclei [math]\sigma_{\gamma}[/math] (barn) [math]\lambda \left (\frac{1}{s} \right)[/math]
Y-88 898 [math] 3.148 \pm 0.012[/math] [math]0.7645 \pm 0.0035[/math] 7.53e-8
1836.1 [math]1.921 \pm 0.0006[/math]
Ni-57 1377.63 [math]0.4542 \pm 0.015[/math] 1.188 5.41e-6
511 [math]17.5 \pm 0.19[/math]
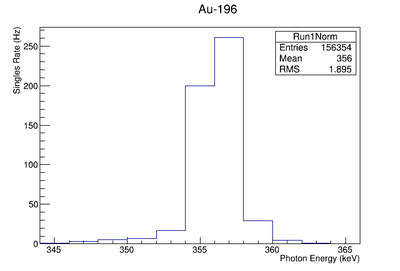
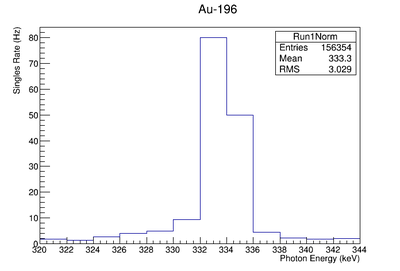
Au-196 355.73 [math]503.6 \pm 3.95[/math] 5.886 1.30e-6
333.03 [math]138.3 \pm 2.18[/math]
[math]t_i[/math] = 5 hr =18000 s
[math]t_d[/math] = 5 days = 432000 s


Y-88 898line.pngY-88 1836line.png

Ni-57 1378line.pngNi-57 511line.png

Au-196 356line.pngAu-196 333line.png


File:Photonuclear xsections.pdf


Cross sections MeV.png


Nickel normalization

Reaction

Ni-08-22-13

Run list

PAA_11-11-13

Photon absorption cross sections:

Ni-58 plot data table

Ni-60 http://www.nndc.bnl.gov/sigma/getPlot.jsp?evalid=15652&mf=3&mt=5&nsub=0

Ni-61 http://www.nndc.bnl.gov/sigma/getPlot.jsp?evalid=15653&mf=3&mt=5&nsub=0

Ni-62 http://www.nndc.bnl.gov/sigma/getPlot.jsp?evalid=15654&mf=3&mt=5&nsub=0

Ni-64 http://www.nndc.bnl.gov/sigma/getPlot.jsp?evalid=15655&mf=3&mt=5&nsub=0

according to pg 13.3 on gets the total cross section by adding up the cross section in the tables up to the desired energy.

http://www.bnl.gov/isd/documents/70393.pdf

Gold normalization

Reaction:

Naturally occurring Isotopes of Gold are Au-197 ( 100% )

Neutron knockout:

Au-197 ->Au-196 has the following lines in order of decreasing intensity: 355.73, 333.03 , half life =9.6 hours, 6.167 days

Proton knockout:

Goes to a stable isotope

NP knockout:

Au-197->Pt-195 no high intensity lines above 100 keV , half life = 4.010 days

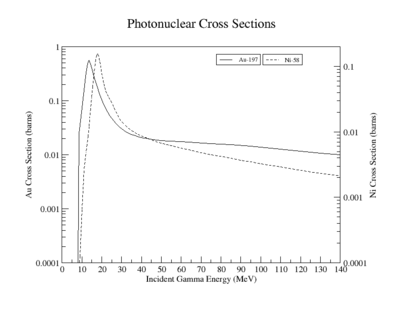
Photon absorption cross sections:

Au-197

plot data table

1836.1 Analysis

The raw Histograms and fits may be found here A_W_thesis_old#1836_keV_signal_table

The Measured half life is

Y-88 Half-life

Days [math]T_{1/2}[/math] Trig Integral Statistical Error Systematic Error Systematic Error without Coincidence Energy Cut
108 1.01 sing 0.8414 [math]\pm 0.048 [/math] [math]\pm 0.021[/math] N/A
coin 0.0062 [math]\pm 3.13e-4 [/math] [math] {+3.91e-4} \atop { -2.64e-3}[/math] [math] {+1.14e-4} \atop { -1.11e-4}[/math]
159 1.49 sing 0.5015 [math]\pm 0.042 [/math] [math] {+0.028} \atop { -0.026}[/math] N/A
coin 0.0046 [math]\pm 2.37e-4 [/math] [math] {+4.98e-4} \atop { -2.87e-3}[/math] [math] {+6.66e-5} \atop { -7.43e-5}[/math]
229 2.15 sing 0.2822 [math]\pm 0.059[/math] [math] {+0.053} \atop { -0.056}[/math] N/A
coin 0.0062 [math]\pm 4.60e-4[/math] [math] {+1.29e-3} \atop { -6.07e-3}[/math] [math] {+2.39e-4} \atop { -3.63e-4}[/math]
245 2.30 sing 0.2449 [math]\pm 0.032 [/math] [math] {+0.028} \atop { -0.033}[/math] N/A
coin 0.0016 [math]\pm 5.63e-5 [/math] [math] {4.72e-4} \atop { -1.23e-3}[/math] [math] {+1.20e-4} \atop { -1.21e-4}[/math]



Y-88 Halflife Update.png



The signal to noise ratio is

Days [math]T_{1/2}[/math] Trig SNR Statistical Error Systematic Error
108 1.01 sing 42.07 [math]\pm 10.78 (25.62%)[/math] [math] {+1.035} \atop { -1.031}[/math]
coin 40.666 [math]\pm 1.236 (3.04%) [/math] [math] {+0.748} \atop { -0.728}[/math]
159 1.49 sing 21.52 [math]\pm 1.722 (8.23%) [/math] [math] {+1.218} \atop { -1.136}[/math]
coin 30.172 [math]\pm 2.480 (8.22%) [/math] [math] {+0.437} \atop { -0.489}[/math]
229 2.15 sing 4.64 [math]\pm 1.161 (25.03%) [/math] [math] {+0.870} \atop { -0.925}[/math]
coin 40.666 [math]\pm 3.095 (7.61%) [/math] [math] {+1.566} \atop { -2.379}[/math]
245 2.30 sing 5.43 [math]\pm 0.980 (18.05%) [/math] [math] {+0.620} \atop { -0.722}[/math]
coin 0.7569 [math]\pm 0.057 (7.57%) [/math] [math] {+0.0568} \atop { -0.0572}[/math]

For the 1836 keV coincidence signal to noise fit, the last data point was not included. The length of the run and activities in the room, such as the nitrogen tank refilling, during counting caused the peak to be spread over a larger energy range. This also meant that the background noise would be large. The background of the first three data points were averaged.


SNR BW Update.png


The following plot is the signal to noise ratio with only the data points used to obtain a fit.


SNR BW2 Update.png


Energy Trig [math]T_{1/2}[/math] (days) [math]A_0[/math] (before efficiency) (Hz) [math]N_0[/math] (before efficiency) (nuclei) [math]A_0[/math] (after efficiency) (Hz) [math]N_0[/math] (after efficiency) (nuclei) [math]T_{final}[/math] (days) [math]A(t_{final})[/math] (Hz) [math] N(t_{final})[/math] (nuclei) [math]\frac{N(t_{final})}{N_0}[/math]
898 sing 130.39 +/- 26.26 3.081 +/- 0.538 4.096e7 +/- 7.147e6 393.544 +/- 71.131 5.231e9 +/- 9.454e8 383.63 [math] {+202.83} \atop { -119.44}[/math] 32.506 +/- 18.162 4.320e8 +/- 2.414e8 0.0826 +/- 0.0485
coin 108.18 +/- 4.89 0.0154 +/- 0.0003 204958.085 +/- 4201.641 9.125 +/- 0.633 1.213e8 +/- 8.416e6 483.60 [math] {+111.97} \atop { -83.40}[/math] 0.3935 +/- 0.0951 5.230e6 +/- 1.264e6 0.0431 +/- 0.0108
1836.1 sing 106.16 +/- 8.63 2.317 +/- 0.262 3.080e7 +/- 3.480e6 742.929 +/- 87.053 9.874e9 +/- 1.157e9 264.94 [math] {+29.37} \atop { -26.24}[/math] 132.74 +/- 20.938 1.764e9 +/- 2.783e8 0.1787 +/- 0.0351
coin 100.10 +/- 4.0 0.0196 +/- 0.0004 260440.778 +/- 5339.036 10.033 +/- 0.447 1.334e8 +/- 5.946e6 305.63 [math] {+64.72} \atop { -49.63}[/math] 1.376 +/- 0.298 1.829e7 +/- 3.958e6 0.1371 +/- 0.0303


Average [math] N_0[/math]: [math](38.4 \pm 5.29) \times 10^{8}[/math]

Error analysis

1.) rate energy cuts

2.) Energy calibration error

3.) Linear background fit error

4.) Gaussian integration of Signal - background peak

5.) ignorable error from run length time

6.) Coincidence energy cut.

7.) dividing by average background for SNR

8.) correction ratio for 3rd data point

9.) error in half life to find N0 for the detection limit extrapolation

10.) error extrapolation efficiency to higher energy lines for N0 calculation

Energy Window systematic error

The signal is measured by subtracting a count rate that is summed over an energy interval. The choice of this integration interval, energy window, is a source of systematic error. In order to calculate the error associated with the energy window, its range was adjusted based on the statistical variance of the background subtracted count rate fit to a gaussian. The integral was measured for window ranges chosen according to an integer interval of the standard deviation [math] \mu \pm n \sigma [/math], where n = 3,4,5. The difference between the largest and mid-value was taken as the positive standard deviation, and the lowest was used for the standard deviation negative fluctuation. The resulting errors were divided by the signal to obtain a percent error as shown in column 1 of TableXXX.

Energy calibration systematic error

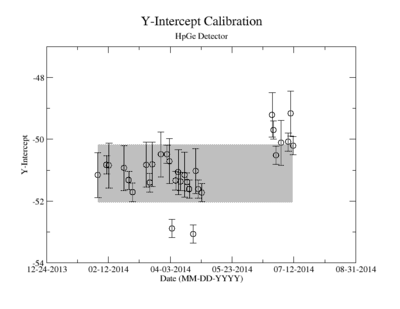
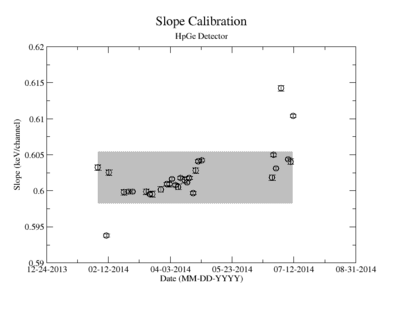
Prior to each measurement of the Y-88 sample's activity, the detectors where calibrated using several standard sources with known activity and dominant energy lines. This was accomplished by counting certified samples of Cs-137, Co-60, and Na-22 as well as Ba-133 and Mn-54. The observed mean ADC channel number was correlated with the expected energy line from each of the above sources. The correlation was measured using a standard linear fit algorithm. The linear fit algorithm determines the uncertainty of each fit parameter, the slope and the y-intercept. The effects of this uncertainty on the signal was analysed and is referred to as the energy calibration error.

YIntCal ADC7 5.png SlopeCal ADC7 5.png

The uncertainty in the energy calibration just before a singles measurement was used to investigate the impact of the calibration on the measured signal for a given energy window of integration. While the singles measurements took less than 10 minutes, the coincidence measurement required more than 24 hours. The long term variance of the energy calibration shown in Figure ZZ.XXX was used to estimate the impact of the energy calibration drift during the coincidence measurements. The fit's y-intercept has a temporal variance corresponding to a relative uncertainty of about 1.865%; the slope is about 0.608%. The effects of this error on the coincidence signal were analysed. In both cases, the range of the energy widow is held constant while the slope and the y-intercept where adjusted to account for all possible combinations with and without their respective uncertainty. The integral value was recorded after every fit parameter change and the max, min, and mean values were obtained. The difference between the largest and mean value was taken as the positive standard deviation, and the lowest was used for the standard deviation's negative fluctuation. The resulting errors were divided by the signal to obtain a percent error as shown in column 2 of TableXXX.

Linear Fit Systematic error

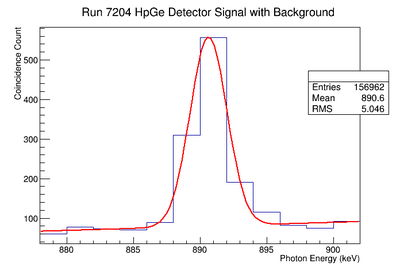
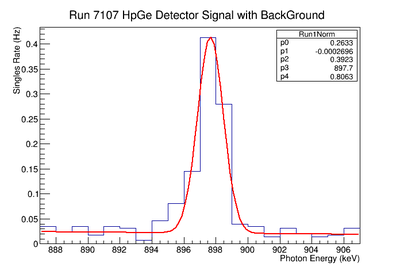
Run7107 898 raw.png

The signal is determine by subtracting the underlying background. A estimate of this background is made by fitting the observed count rate with the function below :

[math] f(x)=A \textstyle \int_{\mu-2\sigma}^{\mu+2\sigma} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2} \operatorname{d}\!x +B x +C[/math].

The above function contains a Gaussian representing the measured signal and a linear function for the background. The above figure XX.YY shows the fit applied. The linear fit parameters are used to create a histogram that is subtracted from the raw signal histogram, resulting in a histogram of just a signal. The energy window range used for the fit was adjusted and several fits performed to determine the uncertainty of the fit's slope and y-intercept. This systematic error, based on the fits dependence on the energy window is shown in the table under the column labeled "Linear Fit of Background". The fit parameters where adjusted to determine the maximum and minimum area of the background. For minimum background area, it was required that the area be positive. The difference between the maximum and unadjusted area value was taken as the positive standard deviation's fluctuation, and the minimum was used for the standard deviation's negative fluctuation. The resulting errors were divided by the signal to obtain a percent error as shown in column 3 of TableXXX.

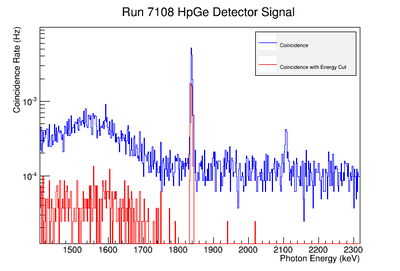
Systematic error of the Coincidence Energy Cut

Figure AAA.XXX below show the coincidence measurements made before(blue) and after(red) energy cuts are applied on the NaI signal to reduce the accidental coincidence events and photons that fail to deposit all their energy in the NaI detector due to compton scattering.

Run7108 CoinOverlay.png Run7108 1836 CoinOverlay.png

To analyze the error association with coincidence counting only, the signal on the NaI detector was fit to a gaussian distribution. The [math]\sigma[/math] of the gaussian fit was used to adjust the energy cut limits. The energy window was set at [math]\text{lower/upper limit} \pm \sigma [/math]. The intergal values were recorded for each instance and the difference between the maximum and unadjusted integral values were taken as the positive standard deviation's fluctuation while the minimums were used for the standard deviation's negative fluctuation. The resulting errors were divided by the coincidence signal to obtain a percent error as shown in column 5 of TableXXX. The limited energy resolution of the NaI detector makes this uncertainty the dominant systematic error. If two HpGe detectors are used, then this uncertainty would decrease substantially will be far less than the remaining dominant systematic error; the energy Gaussian integral uncertainty. We report this systematic uncertainty but it is not propagated for the final result in order consider the case of a coincidence apparatus using two HpGe detectors.


Half-life

898 keV Singles

Days [math]T_{1/2}[/math] Trig Energy Window Energy Calibration Linear Fit of Background Gaussian Integration of Signal Total Systematic Error
108 1.01 sing [math] {+0.367%} \atop { -0.660%}[/math] [math] {+1.026%} \atop { -1.83%}[/math] [math]\pm 0.183%[/math] [math]\pm 5.132%[/math] [math] {+5.32%} \atop { -5.71%}[/math]
159 1.49 sing [math] {+0.713%} \atop { -3.68%}[/math] [math] {+0.816%} \atop { -2.438%}[/math] [math] {+0.747%} \atop { -0.724%}[/math] [math]\pm 6.29%[/math] [math] {+6.52%} \atop { -8.80%}[/math]
229 2.15 sing [math] {+32.83%} \atop { -23.83%}[/math] [math] {+11.87%} \atop { -16.35%}[/math] [math] {+2.7%} \atop { -2.58%}[/math] [math]\pm 3.68%[/math] [math] {+44.94%} \atop { -40.44%}[/math]
245 2.30 sing [math] {+1.19%} \atop { -8.28%}[/math] [math] {+4.24%} \atop { -12.0%}[/math] [math]\pm 1.72%[/math] [math]\pm 10.68%[/math] [math] {+12.1%} \atop { -22.99%}[/math]


898 keV Coincidence

Days [math]T_{1/2}[/math] Trig Energy Window Energy Calibration Linear Fit of Background Gaussian Integration of Signal Coincidence Energy Total Systematic Error Systematic Error without Coincidence Energy Cut
108 1.01 coin [math] {+0.56%} \atop { -0.404%}[/math] [math] \pm 0.31%[/math] [math] {+0.142%} \atop { -0.136%}[/math] [math]\pm 3.46%[/math] [math] {+10.92%} \atop { -33.65%}[/math] [math] {+12.29%} \atop { -34.62%}[/math] [math] {+3.58%} \atop { -3.54%}[/math]
159 1.49 coin [math] {+0.405%} \atop { -0.048%}[/math] [math] \pm 0.38%[/math] [math] {+0.048%} \atop { -0.047%}[/math] [math]\pm 1.81%[/math] [math] {+9.6%} \atop { -14.8%}[/math] [math] {+10.55%} \atop { -15.36%}[/math] [math] {+1.98%} \atop { -1.86%}[/math]
229 2.25 coin [math] {+0.588%} \atop { -3.12%}[/math] [math] {+1.03%} \atop { -2.0%}[/math] [math] {+0.237%} \atop { -0.231%}[/math] [math]\pm 3.82%[/math] [math] {+14.5%} \atop { -31.2%}[/math] [math] {+16.53%} \atop { -36.47%}[/math] [math] {+4.15%} \atop { -6.38%}[/math]
245 2.30 coin [math] {+0.2%} \atop { -0.067%}[/math] [math] {+0.13%} \atop { -0.53%}[/math] [math] {+0.296%} \atop { -0.291%}[/math] [math]\pm 0.719%[/math] [math] {+24.2%} \atop { -101.3%}[/math] [math] {+24.53%} \atop { -102.0%}[/math] [math] {+0.847%} \atop { -0.98%}[/math]


1836.1 keV Singles

Days [math]T_{1/2}[/math] Trig Energy Window Energy Calibration Linear Fit of Background Gaussian Integration of Signal Total Systematic Error
108 1.01 sing [math] {+0.119%} \atop { -0.095%}[/math] [math]\pm 0.33%[/math] [math] {+0.606%} \atop { -0.582%}[/math] [math]\pm 2.34%[/math] [math] {+2.46%} \atop { -2.45%}[/math]
159 1.49 sing [math] {+0.199%} \atop { -0.798%}[/math] [math] {+2.81%} \atop { -1.42%}[/math] [math]\pm 0.279%[/math] [math]\pm 4.79%[/math] [math] {+5.66%} \atop { -5.28%}[/math]
229 2.15 sing [math] {+10.21%} \atop { -7.48%}[/math] [math] {+4.32%} \atop { -8.65%}[/math] [math] {+3.26%} \atop { -3.01%}[/math] [math] {+11.37%} \atop { -11.34%}[/math] [math] {+18.74%} \atop { -19.94%}[/math]
245 2.30 sing [math] {+0.245%} \atop { -5.31%}[/math] [math]\pm 1.674%[/math] [math] {+2.246%} \atop { -2.205%}[/math] [math] {+11.025%} \atop { -11.107%}[/math] [math] {+11.414%} \atop { -13.303%}[/math]


1836.1 keV Coincidence

Days [math]T_{1/2}[/math] Trig Energy Window Energy Calibration Linear Fit of Background Gaussian Integration of Signal Coincidence Energy Cut Total Systematic Error Systematic Error without Coincidence Energy Cut
108 1.01 coin [math] {+0.613%} \atop { -0.55%}[/math] [math] {+0.52%} \atop { -0.5%}[/math] [math]\pm 0.04%[/math] [math]\pm 1.45%[/math] [math] {+5.02%} \atop { -41.45%}[/math] [math] {+6.31%} \atop { -42.58%}[/math] [math] {+1.84%} \atop { -1.79%}[/math]
159 1.49 coin [math] {+0.435%} \atop { -0.196%}[/math] [math] {+0.261%} \atop { -0.804%}[/math] [math] {+0.074%} \atop { -0.073% }[/math] [math]\pm 1.267%[/math] [math] {+10.07%} \atop { -61.3%}[/math] [math] {+10.83%} \atop { -62.39%}[/math] [math] {+1.45%} \atop { -1.62%}[/math]
229 2.15 coin [math] {+0.629%} \atop { -2.55%}[/math] [math] {+1.11%} \atop { -2.19%}[/math] [math] {+0.244%} \atop { -0.239%}[/math] [math]\pm 3.44%[/math] [math] {+18.71%} \atop { -93.06%}[/math] [math] {+20.81%} \atop { -97.90%}[/math] [math] {+3.85%} \atop { -5.85%}[/math]
245 2.30 coin [math] {+0.125%} \atop { -0.438%}[/math] [math] \pm 0.188%[/math] [math]\pm 0.386% [/math] [math]\pm 7.5% [/math] [math] {+28.2%} \atop { -75.6%}[/math] [math] {29.5%} \atop { -76.88%}[/math] [math] {+7.5%} \atop { -7.56%}[/math]


Systematic error in the SNR

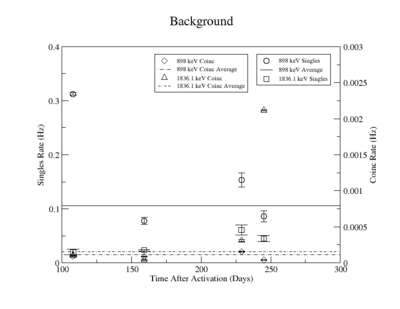
The singles measurement of the 898 keV peak had an initial high background that decays quickly and was more or less constant for singles measurements take 159 days after irradiation. We assumed that this reflected the presence of activated material with half lives longer that 245 days. As a result the background for the last three measurements was averaged and used in the denominator for the SNR. The first singles measurement has a large background due to activated nuclei with short half lives. This background decreased substantially after about 51 days when the next measurement was taken (the half-life of Y-88 is 106.6 days). The singles background near the 1836 keV line was measured to be around 0.5 Hz and fluctuated less over the experiment compared to the background around the 898 peak. The coincidence measurements had such little background, due to the nature of the apparatus, that the background was averaged over the first three measurements for both the 898 and the 1836 peaks separately. The background for the final coincidence measurements was ignored because of the increased noise produced when the detectors nitrogen dewar was filled during the 5 day background measurement.

Background Update.png

The systematic uncertainty of the background was not analysed and propagated into the final SNR uncertainty. The signal's total systematic error, described above, was used for the final uncertainty.


Signal to Noise Ratio

Energy (keV) Trig Variance of Averaged Background
898 sing [math]\pm 39.16%[/math]
coin [math]\pm 50.48%[/math]
1836.1 sing N/A
coin [math]\pm 153.50%[/math]

The background's systematic error is being ignored.

Background contribution to the SNR error

The analysis of the background uncertainty is described in the above section, "Linear Fit Systematic error." The background's relative statistical uncertainty shown in column 5 of TableXXX is calculated by varying the integral of the background by the uncertainties from the fit and dividing by the background used for the SNR ratio calculation. Column 6 presents the uncertainty of the averaged background as mentioned in the previous section. The variance the coincidence measurement is considerable larger than the individual coincidence measurements. The background in each singles measurement is smaller than the average variance indicating that the individual background measurements could have been made longer to improve their statistical uncertainty.

898 keV Background

Days [math]T_{1/2}[/math] Trig Background Linear Fit of Background Error Statistical Error of Averaged Background
108 1.01 sing 0.3123 [math]\pm 0.801%[/math] N/A
coin 9.518e-5 [math] {+7.73%} \atop { -7.45%}[/math] [math]\pm 50.01%[/math]
159 1.49 sing 0.0777 [math] {+8.37%} \atop { -8.11%}[/math] [math]\pm 5.9%[/math]
coin 8.732e-5 [math] {+2.30%} \atop { -2.28%}[/math] [math]\pm 54.51%[/math]
229 2.15 sing 0.1532 [math] {+8.36%} \atop { -7.96%}[/math] [math]\pm 3.0%[/math]
coin 1.554e-4 [math] {+5.17%} \atop { -5.06%}[/math] [math]\pm 30.63%[/math]
245 2.30 sing 0.0862 [math]\pm 11.60%[/math] [math]\pm 5.3%[/math]
coin 3.948e-5 [math] {+11.24%} \atop { -11.06%}[/math] [math]\pm 120.57%[/math]

1836 keV Background

Days [math]T_{1/2}[/math] Trig Background Linear Fit of Background Error Statistical Error
108 1.01 coin 1.037e-4 [math] {+2.42%} \atop { -2.39% }[/math] [math]\pm 951.78%[/math]
159 1.49 coin 4.248e-5 [math] {+8.06%} \atop { -7.88% }[/math] [math]\pm 232.34%[/math]
229 2.15 coin 3.112e-4 [math] {+4.87%} \atop { -4.76%}[/math] [math]\pm 317.16%[/math]
245 2.30 coin 2.114e-3 [math]\pm 0.29% [/math] [math]\pm 46.69%[/math]


Singles Efficiency on 2/28/2014

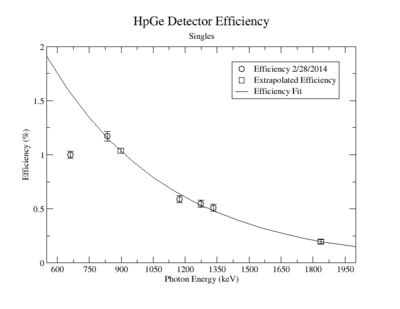
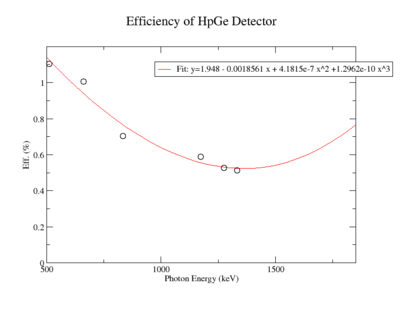
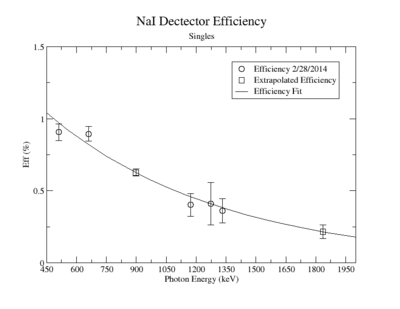
A measurement of the HpGe detectors geometric efficiency for detecting the Y-88 energy lines at 898 keV and 1836.1 keV was performed in order to determine the absolute activity of the sample. The count rate for several sources of known activity was measured by the data acquisition system. Since each sample has decayed since the original calibration by the source vendor, column 4 of tableXX.YY. reports the expected rates from each calibrated sample that were calculated using the half life and the known activity of the standard sources. The characteristic energy peaks from each source was fit to a gaussian distribution. The variance from that fit was used to determine the range of integration for the count rate measurement. The integration energy range was selected to include counts over the energy interval from [math]\bar{E} - (2\sigma+\Delta \sigma)[/math] to [math]\bar{E} + (2\sigma+\Delta \sigma)[/math]. The measured rates for each calibrated source using the HpGe detector are listed in column 5. The efficiency given by the ratio of the rates in column 5 to the expected rates in column 4 are shown in column 6 of the same table. The percent efficiency of the standard sources was fit to a exponential curve shown in figureXX.YY. The singles efficiency for 898 keV and 1836.1 keV were extrapolated from the exponential equation and are recorded in tableXX.YY. This process was repeated for the NaI detector and the results can be seen in figureXX.YY and tablesXX.YY and XX.YY.


HpGe Detector

Run Source Energy Expected rate (Hz) HpGe Det B Rate (ADC 7) (Hz) HpGe Eff (%)
7027 Na-22 511 1589.218 +/- 49.425 18.07 +/- 0.111 1.137 +/- 0.0317
7025 Cs-137 661.657 2548.03 +/- 80.008 25.468+/- 0.172 0.9995 +/- 0.0321
7029 Mn-54 834.848 41.405 +/- 1.300 0.485 +/- 0.014 1.171 +/- 0.0427
7026 Co-60 1173.228 1876.619 +/- 58.926 11.03 +/- 0.106 0.588 +/- 0.0328
7027 Na-22 1274.537 888.264 +/- 27.625 4.857 +/- 0.034 0.5468 +/- 0.0319
7026 Co-60 1332.492 1878.167 +/- 58.974 9.584 +/- 0.023 0.510 +/- 0.0315 


  1  Constant     6.36491e-01   4.70444e-02   1.00271e-05  -3.28621e-03
  2  Slope       -9.81232e-04   5.68236e-05   1.21109e-08  -1.59453e+00


SingEff NoMn.png


Extrapolated Efficiency

Source Energy HpGe Eff (%)
Y-88 898 0.7830 +/- 0.0471
Y-88 1836.1 0.3119 +/- 0.0310

NaI Detector

Run Source Energy Expected rate (Hz) NaI Det B Rate (ADC 7) (Hz) NaI Eff (%)
7027 Na-22 511 1589.218 +/- 49.425 14.393 +/- 0.715 0.9057 +/- 0.0586
7025 Cs-137 661.657 2548.03 +/- 80.008 22.8 +/- 0.9154 0.8948 +/- 0.0510
7026 Co-60 1173.228 1876.619 +/- 58.926 7.529 +/- 0.5503 0.4012 +/- 0.0796
7027 Na-22 1274.537 888.264 +/- 27.625 3.654 +/- 0.5266 0.4114 +/- 0.1474
7026 Co-60 1332.492 1878.167 +/- 58.974 6.784 +/- 0.5345 0.3612 +/- 0.0848


SingEffNaI corrected.png


Source Energy NaI Eff (%)
Y-88 898 0.6262 +/- 0.0246
Y-88 1836.1 0.2158 +/- 0.0466

Coincidence Efficiency

Unlike the singles efficiency found above, the efficiency for a coincidence measurement relies on the combined efficiency of both detectors. A known Y-88 source was not available to measure the coincidence activity directly. Instead, the HpGe's geometric efficiency for detecting the Y-88 energy lines at 898 keV and 1836.1 keV was combined with the NaI detectors efficiency for the 1836.1 and 898 keV lines respectively. For example, to obtain the 898 keV coincidence efficiency, the HpGe singles efficiency at this energy line is multiplied by the NaI singles efficiency at the 1836.1 keV line. The uncertainties of the singles efficiency are added in quadrature and the resulting values recorded in column 4 of tableXX.YY. The reverse case was applied to find the coincidence efficiency at the 1836.1 keV line and the values are listed in column 4 of tableXX.YY.


Source HpGe Singles 898 keV Eff (%) NaI Singles 1836.1 keV Eff (%) HpGe Coincidence Eff (%)
Y-88 0.7830 +/- 0.0471 0.2158 +/- 0.0466 0.1690 +/- 0.0663


Source HpGe Singles 1836.1 keV Eff (%) NaI Singles 898 keV Eff (%) HpGe Coincidence Eff (%)
Y-88 0.3119 +/- 0.0310 0.6262 +/- 0.0246 0.1953 +/- 0.0396


A_W_thesis

Retrieved from "https://wiki.iac.isu.edu/index.php?title=A_W_thesis_old&oldid=100933"