TF EIM Chapt1

Fundamentals

Charge

Every stable and independent object (particle) that has charge has been observed to contain a quantized unit of charge which is a multiple of [math]1.6 \times 10^{-19} \mbox{Coulombs}[/math]

What are the obervations/experiments?

Experiment 1: Matter is composed of Atoms with a positively charged nucleus surround by negatively charged electrons. If we now the charge of one mole of electrons ([math]F[/math]= Faradays constant) and the number of electrons in a mole ([math]N_A[/math] = Avagadros number)then the charge of a single electron is given by

[math]e = \frac{F}{N_A}[/math]

Experiment 2: Oil drop experiment

http://www.youtube.com/watch?v=XMfYHag7Liw&feature=player_embedded

Experiment 3: The Hall Effect and the Josephson Effect

Coulomb

The amount of charge that flows through any cross section of a wire in 1 second if there is a steady current of 1 ampere in the wire.

Coulomb Force

Two charged object separated by a distance (d) will feel a force between them known as the coulomb force. The magnitude of this force has been experimentally shown to be

[math]\left | \vec{F}_{coul} \right | = \frac{1}{4 \pi \epsilon_0} \frac{q_1 q_2}{r^2}[/math]

where

[math] \varepsilon_0 =\frac {1}{\mu_0 c_0^2}=8.854187817 \times 10^{-12}[/math]F/m = a experimentally measured quantity satisfying the above relationship know as the permittivity of free space.

[math] q_1 =[/math] charge of first object

[math]q_2 =[/math] charge of second object

[math]r =[/math] distance between the charges

(Charles Augustin Coulomb first measured the attract and repulsive force between two charged objects using a torsion balance around 1785)

This force may be described in terms of an electric field E such that

[math]\vec{E} = \frac{\vec{F_q}}{q}[/math]

Where

F= force between the objects

Electric Field

Vector Field

What is a vector field?

A vector field is the association of each point in space with a direction (vector).

Example: Gravity. On the surface of the earth you observe that an apple will fall down to the ground. You can measure the magnitude of this force by observing the attraction much like how coulomb observed how two charges attract or repel each other. You can define a vector ([math]\vec{g})[/math] which points directly down and tell you the direction that an apple will accelerate if it is released. If you construct [math]\vec{g}[/math] such that

[math]\vec{g} = \frac{F_g}{m} = \frac{\frac{GMm\vec{r}}{r^3}}{m} = \frac{GM\hat{r}}{r^2}[/math] = acceleration of an apple towards the earth's surface when close to the earth's surface.

Where G= gravitational constant = [math]6.67 \times 10^{-11} \frac{N m^2}{kg^2}[/math]

Electric Field Vector

Electric Field	Grass seeds in Insulating Liquid
Electric Vector Field for an infinitely long sheet of negative charge. The vector direction indicates the direction a positive test charge will move	The orientation of Grass seeds immersed in an insulating liquid with a charged plate. The grass seeds become polarized and align with the electric field

Instead of an apple of mass [math](m)[/math] we can use a test charge of charge [math](q_0)[/math].

Instead an earth of mass [math](M)[/math] we can use an object of charge [math](Q)[/math].

We now define an Electric field Vector [math](\vec{E})[/math] such that

[math]\vec{E} = \frac{\vec{F}_q}{q_0} [/math] ;Notice the direction tells you which way a positive charge will move

Note

The definition of [math]\vec{E}[/math] requires that the magnitude of the test charge approach zero, because the test charge can disturb the electric field we are actually trying to determine.

[math]\vec{E} = \lim_{q_0 \rightarrow 0} \frac{\vec{F}_q}{q_0} = \lim_{q_0 \rightarrow 0} \frac{\frac{1}{4 \pi \varepsilon_o} \frac{Q q_0 \vec{r}}{r^3}}{q_0} = \frac{1}{4 \pi \varepsilon_o} \frac{Q \hat{r}}{r^2}[/math]

Lines of Coulomb Force

Once you know the Electric Vector Field you know the force on any charge placed in that field simply by

[math]\vec{F} = q \vec{E}[/math]

In other words, the tangent to the direction of the Force vector indicates the direction of the vector field [math]\vec{E}[/math].

Unfortunately, charge can be either positive or negative whereas mass is always a positive quantity so the above uses the convention of a positive (test) charge.

Electric potential

The Electric potential (V) is a scalar which may be used to describe Electric Fields as well.

A charge which moves along an electric field line is having work done on it by an electric field.

Electric Potential Energy

From the work energy theorem, Work is equal to the change in energy of a system

[math]W = \Delta[/math] Energy

The work done moving a change along an electric field line is

[math]W = \int \vec{F} \cdot d\vec{r} = \int q \vec{E} \cdot d\vec{r} \equiv [/math] Potential Energy

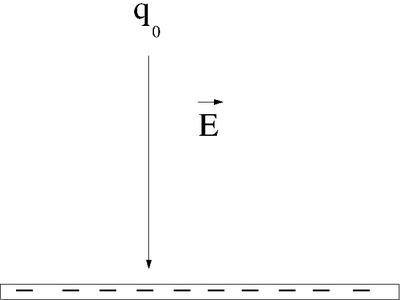
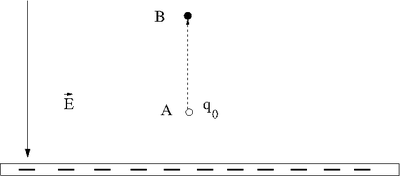
Let's say you lift a unit of POSITIVE charge (q) from location A above a sheet of negative charge to a higher location B.

Note

This is just like the gravitational example of walking up a flight of stairs.

You will need to apply a force on the positive charge to lift it up because the negatively charge sheet is attracting it (like the earth attracts your mass as you walk up a flight of stairs). For simplicity, let's assume you move at a constant velocity or no acceleration. In other words the attractive coulomb force is balanced by the force you use to push the positive charge to a higher location above the negatively charged infinite sheet.

[math]W = \int_A^B \vec{F} \cdot d\vec{r} [/math] Potential Energy

[math]=\int_A^B q (-\vec{E}) \cdot d\vec{r} =-\int_A^B q \vec{E} \cdot d\vec{r} [/math]

[math](-\vec{E} \cdot d\vec{r}) = \left | \vec{E} \right | dr[/math] : The applied force is directed opposite to the Electric field but in the same direction as the displacement[math] \vec{r}[/math]

[math]=\int_A^B \left | \vec{E} \right | dr = \Delta U = U_B - U_A[/math] = Potential Energy Difference

Note

The work done by the electric field is negative (the force from the electric field is opposite to the direction of motion).

Voltage (Electric Potential)

The Electric Potential Difference[math] \equiv \Delta V = V_B - V_A = \frac{\Delta U}{q_0} = \int_A^B Edr = \frac{W}{q_0}[/math]

The change in the potential depends on the sign of q_0

Positive (Negative) charge naturally goes from higher (lower) potential to lower (higher) voltage.

Voltage decreases(increases) when you travel parallel(anti-parallel) to the electric field.

When you measure the electric potential (Voltage) you are actually measuring a potential difference[math] \Delta[/math] V with respect to some point [math]V_A[/math] that is customarily chosen to be zero.

Remember this when you place the black probe of your voltmeter onto some 
conducting point. The black probe might not be at "ground".

If you define the potential [math]V_A[/math] to be zero and move the charge a distance [math]d[/math] then the voltage is given by

V = V_B = Ed

Electromotive Force(emf)

An electromotive force is used to describe the external work expended per unit of charge to produce an electric potential difference across two open-circuited terminals.

Battery

A battery uses a chemical reaction to separate atoms into ions and push electrons onto the negative terminal. The terminal of a battery are usually made out of two different metal electrodes separated by a solution/paste containing ions called the "electrolyte".

Ex: Carbon and zinc electrodes separated by ammonium chloride results in a chemical reaction which generates a 1.5 Volt potential difference between the carbon and zinc electrodes. This is called a cell. From cells you can make batteries by tying cells in series or parallel.

Bat. Type	Cell emf (V)	characteristic
Carbon-Zinc	1.5	flashlight battery, voltage drops slowly with time
Alkaline-Maganeses	1.5	long lasting lasting flashlight battery, high current capacity, voltage drops gradually
Nickel-cadmium	1.25	rechargeable flashlight battery
Lead-acid	2.6	car battery, high currents, rechargeable, sufluric acid electrolyte
Silver Oxide	1.5	hearing aids and wathes, low current, constant voltage
Mercury	1.35	sudden voltage drops, indoor equipment.

Notice the battery is an isolated voltage source. This means the definition of zero potential can be made at any one point in a circuit with one battery. Because the battery is using a chemical reaction, the electrons come from inside the battery and are not pulled or pushed from the earth (a ground).

As soon as you use the battery the emf changes and is called a voltage because of the internal resistance of the battery (see Lab 1). The voltage rating of the battery represents its "open-circuit" voltage; the voltage when it is not connected.

Unfortunately, batteries have an internal voltage which is only negligible if the external circuits resistance is much larger then the battery's internal resistance. When a battery is "dead" its internal resistance has become equivalent to the circuit the battery is trying to drive (flashlight). The chemical reaction has ceased to effectively pump electrons onto the terminal and as a result "resists" current flow.

Ohm's Law

resistance is a constant

[math]R = \frac{\Delta V}{I}[/math]= constant

Voltage

The MKS unit for Voltage is a Joule per Coulomb [math]\left ( \frac{\mbox{J}}{\mbox{C}}\right )[/math]

Voltage in circuits is typically defined as the electric potential energy per unit charge relative to ground.

Kirhcoff's Laws

Forest_Electronic_Instrumentation_and_Measurement