Difference between revisions of "Neutron Polarimeter"
Jump to navigation
Jump to search
| Line 16: | Line 16: | ||
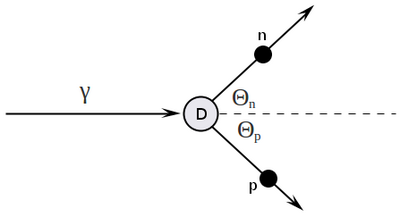
<math> p_D = \left( m_D,\ 0,\ 0,\ 0 \right) </math> | <math> p_D = \left( m_D,\ 0,\ 0,\ 0 \right) </math> | ||
<math> p_{n} = \left( E_n,\ p_n\cos(\Theta_{n}),\ p_n\sin(\Theta_{n}),\ 0 \right) </math> | <math> p_{n} = \left( E_n,\ p_n\cos(\Theta_{n}),\ p_n\sin(\Theta_{n}),\ 0 \right) </math> | ||
| − | <math> p_{ | + | <math> p_{p} = \left( E_p,\ p_p\cos(\Theta_{p}),\ p_p\sin(\Theta_{p}),\ 0 \right) </math> |
<math> p^{\mu}_{\gamma} + p^{\mu}_{D} = p^{\mu}_{p} + p^{\mu}_{n} </math> | <math> p^{\mu}_{\gamma} + p^{\mu}_{D} = p^{\mu}_{p} + p^{\mu}_{n} </math> | ||