Difference between revisions of "Faraday Cup Analysis"
| Line 66: | Line 66: | ||
:: <math>\sigma = \sqrt{\mu}</math> | :: <math>\sigma = \sqrt{\mu}</math> | ||
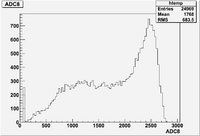
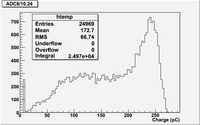
| + | The histogram shows | ||
| + | |||
| + | :Mean = <math>176.7 =\frac{\sum_i^N x_i}{N}</math> | ||
| + | :RMS = | ||
[http://wiki.iac.isu.edu/index.php/FC_Analysis Go Up] | [http://wiki.iac.isu.edu/index.php/FC_Analysis Go Up] | ||
[http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | [http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | ||
Revision as of 21:11, 9 April 2010
FC analysis using ADC channel current distribution
For each ADC channel:
For distribution over all ADC channel:
???
FC analysis using pulse by pulse ADC channel mean value distribution
For each beam pulse:
For distribution over all beam pulses:
Here is:
1. ADC# = bridge#
2. Pulse# = ReadOut# = Entry# = Event#
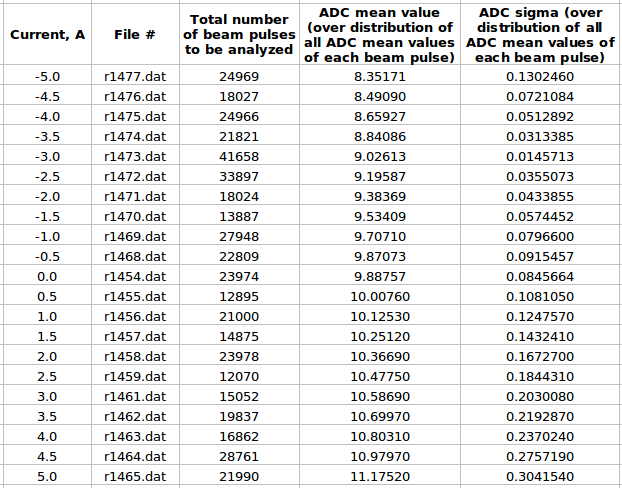
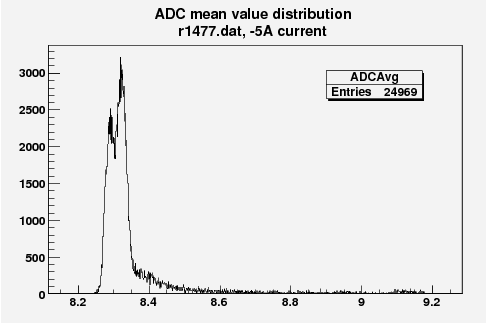
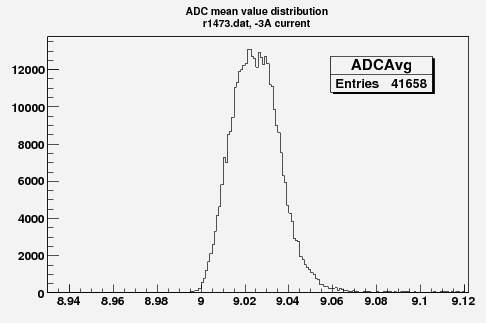
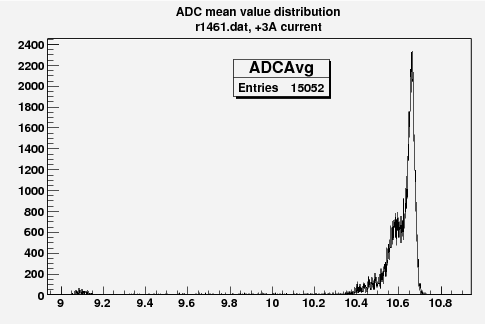
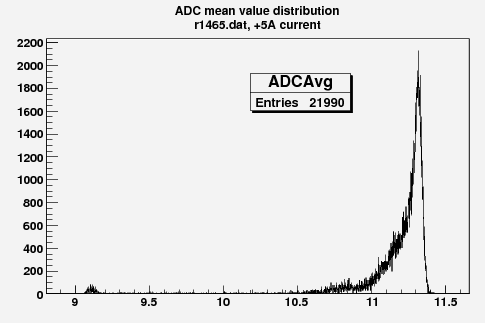
Some examples of ADC mean value distribution. Here are:
1. x axis: ADC mean value for one pulse
2. y axis: number of pulse w/ that ADC mean value
Faraday Cup 3D plot
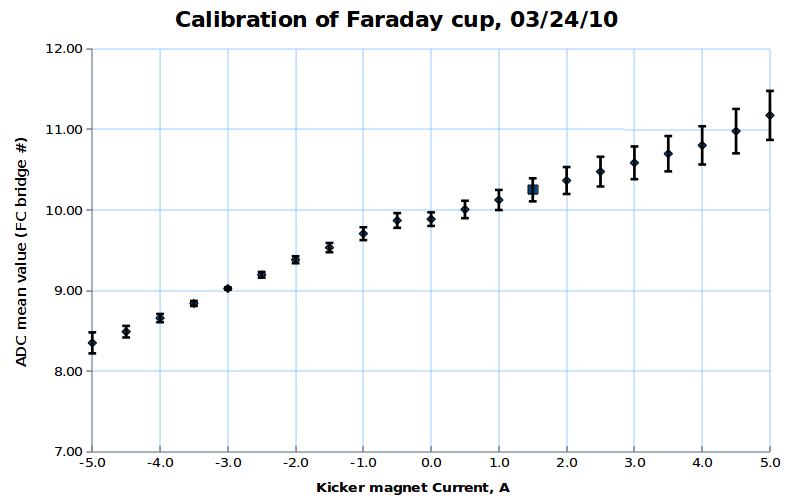
Below is the plot of the charge in Faraday cup (pC) as a function of magnet current (vertical axis, A) (basically magnetic field) and ADC (horizontal axis).
Faraday Cup ADC channel distribution
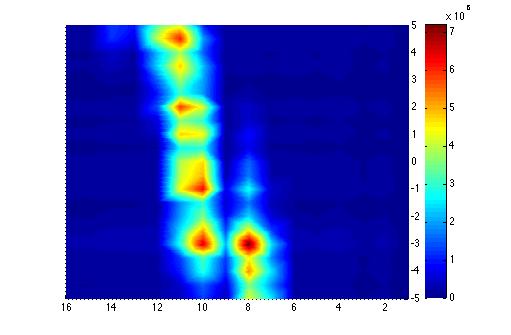
Faraday Cup "Rain"
Error Analysis
The ADC measures the charge deposited on each of the 16 Aluminum blocks. The ADC is a 12 bit ADC with a max input of 400 pc. THe means that the charge per channel is:
Run1477 -5A
Raw ADC result for channel 8 :
ADC 8 using channel -> Coul conversion:
The above histogram shows an RMS of 66.74 pC.
Comment
- The ADC basically counts the number of electrons collected by the aluminum FC bricks and transfered through the cables to the ADC. This is a poisson process with a large number of trials leading to a large mean value . One would expect a gaussian parent population with
The histogram shows
- Mean =
- RMS =