Forest ModernPhysics

Matter Waves (Wave Particle Duality)

Special relativity said that

$E = pc$ if m=0

Plank said he could fit the Black Body radiation data assuming that that

$E= hf$ where $h = 6.63 \times 10^{-34} \mbox{ J} \cdot \mbox{s}$ = Plank's constant

Combining the two we have

$p=\frac{E}{c} = \frac{ h f}{c}$

$\Rightarrow$ photons have momentum like a particle (mv)

Do particles reciprocate and behave like photons?

De Broglie's Hypothesis

If photons can behave like particles by having momentum

Then can a particle behave like a wave by having wavelength

$p=\frac{ h f}{c} = \frac{h}{\lambda}$

or

$\lambda_{particle} = \frac{h}{p}=$ de Broglie Hypothesis

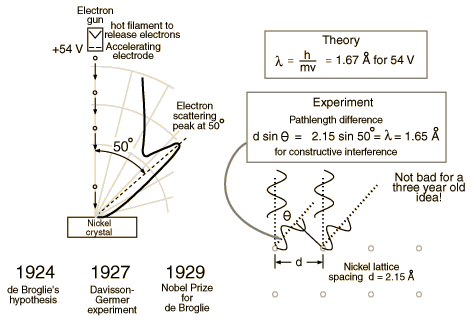
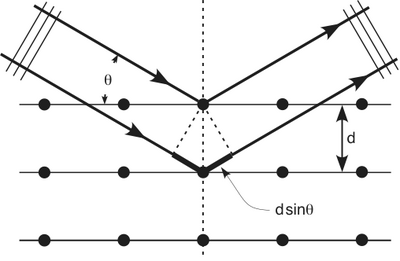
Davisson and Germer

We know that X-rays having a wavelength of $\lambda_{X-rays} = 7.1 \times 10^{-11} \mbox{m}$ make an interference patter on an aluminum foil.

$p_{X-ray} = \frac{h}{\lambda} = \frac{6.63 \times 10^{-34} \mbox{ J} \cdot \mbox{s}}{7.1 \times 10^{-11}\mbox{m}} \frac{1 \mbox{eV}}{1.6 \times 10^{-19} \mbox{J}}$

$= 5.8 \times 10^{-4} \frac{3 \times 10^{8}\mbox{m/s}}{c}$

$= 1.75 \times 10^{4} \frac{\mbox{eV}}{c}$

$= 17.5 \frac{\mbox{keV}}{c}\Rightarrow \mbox{E}=17.5 \mbox{keV}$

Another way to calculate

$p_{X-ray} = \frac{hc}{\lambda c} = \frac{1240\mbox{ eV} \cdot \mbox{nm}}{0.071 \mbox{nm}\cdot \mbox{c}}= 17.5 \frac{\mbox{keV}}{c}$

What would be the energy of an electron with the same wavelength as the above X-ray?

relativistic total energy relation

$E_{tot} = \sqrt{(pc)^2 + (mc^2)^2}$

$= \sqrt{(17.5 keV)^2 + (511 keV)^2}$

= 511.3 keV

relativistic kinetic energy

$K = E - mc^2 = (\gamma-1)mc^2 = 0.3 \mbox{keV} = 300 \mbox{eV}$

Note $\beta = \frac{pc}{E_{tot}} = \frac{17.5 \mbox{keV}}{511 \mbox{keV}} = 0.03 \Rightarrow$ classical physics may be used for electrons below 50 keV

K = \frac{1}{2} mv^2 = \frac{1}{2}\frac{511 \mbox{keV}}{c^2}(0.03 c^2 =

Hit a crystal made of nickel with 54 eV electrons.

1.) 54 eV electrons

From hyperphysics:

Bragg Diffraction

[1] Forest_Classes