Integrated asymmetry

Go Back

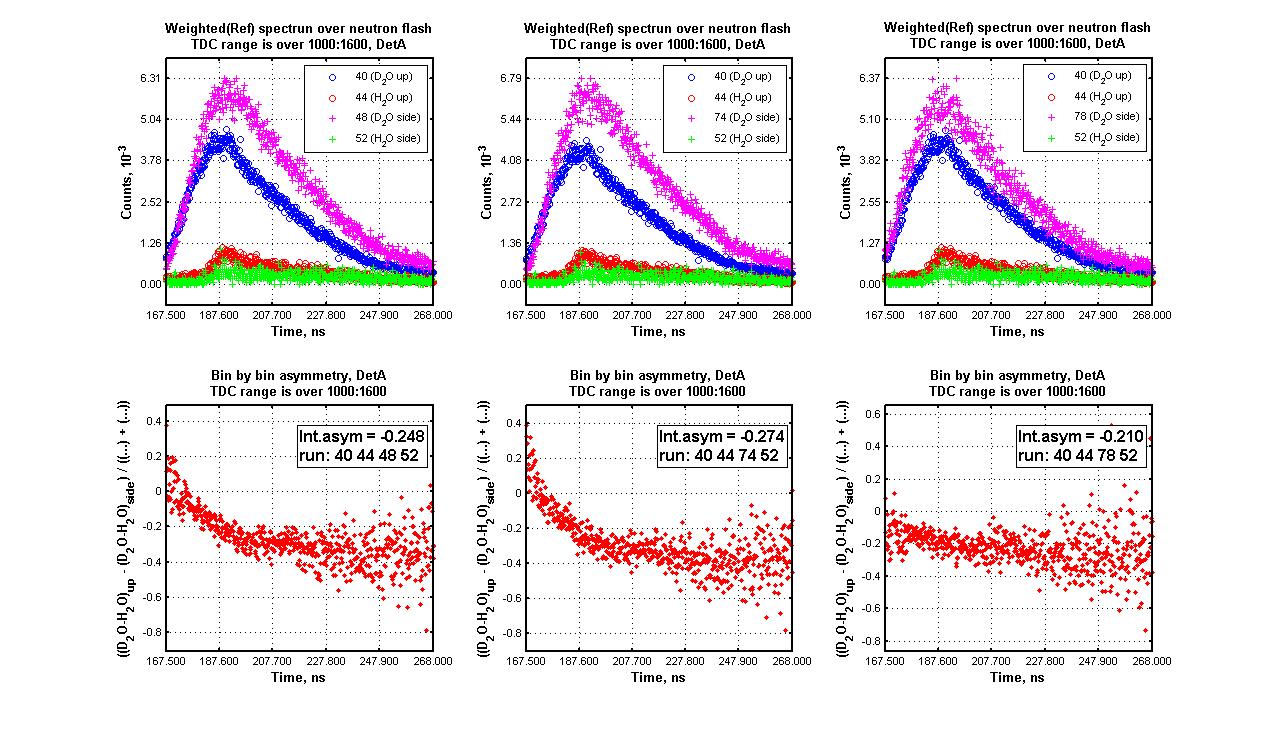
Integrated asymmetry calculation

$Asymm = \frac{\sum \left[\left(\frac{up(ii)}{Wup}-\frac{upbg(ii)}{Wupbg}\right) - \left(\frac{sd(ii)}{Wsd}-\frac{sdbg(ii)}{Wsdbg}\right)\right]} {\sum \left[\left(\frac{up(ii)}{Wup}-\frac{upbg(ii)}{Wupbg}\right) + \left(\frac{sd(ii)}{Wsd}-\frac{sdbg(ii)}{Wsdbg}\right)\right]}$

where

up(ii)   - D2O, detector Up,   Wup - weighted coefficient for up(ii)

upbg(ii) - H2O, detector Up,   Wup - weighted coefficient for upbg(ii)

sd(ii)   - D2O, detector Side, Wup - weighted coefficient for sd(ii)

sdbg(ii) - N2O, detector Side, Wup - weighted coefficient for sdbg(ii)

For detector A summation is over [1000:1600] bin numbers
For detector C summation is over [900:1600] bin numbers

Error calculation

$Error = \sqrt{\left(\frac{\boldsymbol\partial A}{\boldsymbol\partial up}\right)^2(\boldsymbol\delta up)^2 + \left(\frac{\boldsymbol\partial A}{\boldsymbol\partial Wup}\right)^2(\boldsymbol\delta Wup)^2 + ...}$

If assume:
$\boldsymbol\delta up = \sqrt{up};\quad\boldsymbol\delta Wup = \sqrt{Wup};\quad...$

Then
$Error = \sqrt{\left(\frac{(+)-(-)}{(+)^2}\right)\left[\fraq{a}{b}\right]}$

Cases was analysed

Det A:

D2O Up,   files# [40,56,102,108,134,205,210,230];

H2O Up,   files# [44];

D2O Side, files# [48,74,78,82,86,90,94,146,180,190,225,235];

H2O Side, files# [52];

Det C:

D2O Up,   files# [49,75,79,83,87,91,95,147,181,191,226,236];

H2O Up,   files# [53];

D2O Side, files# [41,57,103,107,135,206,211,231];

H2O Side, files# [45];

Results

Table 1: Det A, weighted with [math]{\color{Red}NaI \ detector}[/math]

Table 2: Det C, weighted with [math]{\color{Red}NaI \ detector}[/math]

Table 3: Det A, weighted with [math]{\color{Red}Ref \ detector}[/math]

Table 4: Det C, weighted with [math]{\color{Red}Ref \ detector}[/math]

(File:Asymm table .pdf)

Change the X-axis to nanosecond or neutron energy (TF)

Only one "s" in Asymmetry

Example of bin by bin asymmetry

Go Back