|
|
| Line 88: |
Line 88: |
| | Our list of Lorentz invariants is | | Our list of Lorentz invariants is |
| | | | |
| − | : <math>\left ( p^1 \right )_{\mu} \left (p^1 \right )^{\mu}= \frac{E^2(1)}{c^2} - p^2(1) \equiv E^2 - p^2 = m^2(1)</math>= Lorentz invariant | + | : <math>\left ( p_1 \right )_{\mu} \left (p_1 \right )^{\mu}= \frac{E^2_1}{c^2} - p^2_1 \equiv E^2 - p^2_1 = m^2_1</math>= Lorentz invariant |
| | :p_2^2 = m_2^2 : similarly | | :p_2^2 = m_2^2 : similarly |
| | | | |
| | Let <math>E_{21}</math> = Energy of particle #2 as observed by particle #1 | | Let <math>E_{21}</math> = Energy of particle #2 as observed by particle #1 |
Revision as of 23:32, 30 October 2007
Lorentz Transformations
The picture below represents the relative orientation of two different coordinate systems [math](S, S^{\prime})[/math] . [math]S[/math] is at rest (Lab Frame) and [math]S^{\prime}[/math] is moving at a velocity v to the right with respect to frame [math]S[/math].
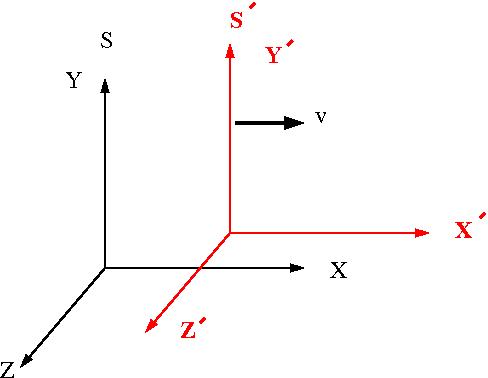
The relationship between the coordinate[math] (x,y,z,ct)[/math] of an object in frame [math]S[/math] to the same object described using the coordinates [math](x^{\prime},y^{\prime},z^{\prime},ct^{\prime})[/math] in frame [math]S^{\prime}[/math] is geven by the Lorentz transformation:
4- vector notation
The 4-vector notation is given as
- [math]x^{\mu^{\prime}} = \sum_{\nu=0}^3 \Lambda_{\nu}^{\mu} x^{\nu}[/math]
where
- [math] x^0 \equiv ct[/math]
- [math]x^1 \equiv x[/math]
- [math]x^2\equiv y[/math]
- [math]x^3\equiv z[/math]
- [math]\Lambda = \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ][/math]
- [math]\beta = \frac{v}{c} = \frac{pc}{E}[/math]
- [math]\gamma = \frac{1}{\sqrt{1 -\beta^2}} = \frac{E_{tot}}{mc^2}[/math]
- NOTE
- It is common in particle physics to define [math] c \equiv 1[/math] making [math]\gamma = \frac{E}{m}[/math] where [math]m[/math] is in units of [math]\frac{\mbox{MeV}}{\mbox{c}^2}[/math]
- example
- [math]x^{0^{\prime}} = \sum_{\nu=0}^2 \Lambda_{\nu}^0 x^{\nu} = \Lambda_0^0 x^0 + \Lambda_1^0 x^1 \Lambda_2^0 x^2 + \Lambda_3^0 x^2[/math]
- [math]ct^{\prime}= \gamma x^0 - \gamma \beta x^1 + 0 x^2 + 0 x^3 = \gamma ct - \gamma \beta x = \gamma(ct -\beta x)[/math]
- Or in matrix form the tranformation looks like
- [math]\left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix} \right )[/math]
- Note
- Einstein's summation convention drops the [math]\sum[/math] symbols and assumes it to exist whenever there is a repeated subscript and uperscript
- ie; [math]x^{\mu^{\prime}} = \Lambda_{\nu}^{\mu} x^{\nu}[/math]
- in the example above the[math] \nu[/math] symbol is repeated thereby indicating a summation over [math]\nu[/math].
Momentum 4-vector
- [math]p^{\mu} \equiv (\frac{E}{c} , \vec{p})[/math]
- [math]p_{\mu} \equiv (\frac{E}{c} , -\vec{p})[/math]
- [math]p_{\mu}p^{\mu} = \frac{E^2}{c^2} - p^2 \equiv E^2 - p^2 = m^2[/math]
- Note
- There is another convention used for 4-vector notation by Perkins and Koller which goes like this
- [math]p^{\mu} \equiv (\vec{p},iE)[/math]
- [math]p_{\mu} \equiv (\vec{p},iE)[/math]
Trig Method
Another way to represent the lorentz transformation is by using the substitution
- [math]\sin (\alpha) \equiv \beta \equiv \frac{v}{c}[/math]
- [math]\cos(\alpha) \equiv \frac{1}{\gamma} \equiv \sqrt{1 - \beta^2}[/math]
- The Matrix form pf the tranformation looks like
- [math]\left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \sec(\alpha) & -\tan(\alpha) & 0 & 0 \\ -\tan(\alpha) & \sec(\alpha) &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix} \right )[/math]
- Or the reverse transformation
- [math]\left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix}\right )= \left [ \begin{matrix} \sec(\alpha) & \tan(\alpha) & 0 & 0 \\ \tan(\alpha) & \sec(\alpha) &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )[/math]
- Notice that you just needed to change the signs for the inverse matrix [math]\Lambda^{-1}[/math]
Proper Time and Length
Proper Time
- Proper Time [math]\Tau[/math]
- The time measured in the rest frame of the clock. The time interval is measured at the same x,y,z coordinates because the clock chose is in a frame which is not moving (rest frame).
The time given in any frame (t) = [math]\gamma \Tau[/math]
- Note
- since [math]\gamma \gt 1[/math] you expect the Proper time interval to be the smallest
Proper Length
- Proper Length[math] (c\Tau)[/math]
- The length of an object in the object's rest frame.
Invariant Length
Transformation Examples
Kinematics in Center of Momentum Frame
In this example we would like to determine the energy of particle #2 as seen from a referenve frame attached to particle # 1, ie; particle #1's rest frame.
Our list of Lorentz invariants is
- [math]\left ( p_1 \right )_{\mu} \left (p_1 \right )^{\mu}= \frac{E^2_1}{c^2} - p^2_1 \equiv E^2 - p^2_1 = m^2_1[/math]= Lorentz invariant
- p_2^2 = m_2^2 : similarly
Let [math]E_{21}[/math] = Energy of particle #2 as observed by particle #1
