|
|
| Line 34: |
Line 34: |
| | | | |
| | =Finding the Cross Section= | | =Finding the Cross Section= |
| − | ==Total cross section== | + | ==Total cross section over φ== |
| | [[File:CrossSectionMathematicaProof.png]] | | [[File:CrossSectionMathematicaProof.png]] |
| | | | |
| | + | ==Total cross section over DC limits== |
| | | | |
| | + | |
| | + | If we make the assumption that the beam of incoming electrons is a flux over an area for a given time, |
| | + | |
| | + | <center><math>N_{incident}=\Phi\ A_{beam}\ t_{run} \rightarrow dN_{incident}=\Phi\ dA_{beam}\ t_{run}\rightarrow\ \frac{dN_{incident}}{ dA_{beam}}=\Phi\ t_{run}</math></center> |
| | + | |
| | + | |
| | + | Using the definition of the differential cross section: |
| | + | |
| | + | <center><math>\frac{d\sigma}{d\Omega}\equiv \frac{ \Biggl(\frac{dN_{scattered}}{d\Omega} \Biggr)}{\Biggl(\frac{dN_{incident}}{dA}\Biggr)}\rightarrow \frac{d\sigma}{d\Omega}\Biggl(\frac{dN_{incident}}{dA}\Biggr)=\Biggl(\frac{dN_{scattered}}{d\Omega} \Biggr)</math></center> |
| | + | |
| | + | |
| | + | Substituting using the flux |
| | + | |
| | + | <center><math> \frac{d\sigma}{d\Omega}\Biggl(\frac{dN_{incident}}{dA}\Biggr)=\Biggl(\frac{dN_{scattered}}{d\Omega} \Biggr)\rightarrow \frac{d\sigma}{d\Omega}\Phi\ t_{run}=\Biggl(\frac{dN_{scattered}}{d\Omega} \Biggr)</math></center> |
| | + | |
| | + | |
| | + | <center><math>\rightarrow dN_{scattered}= \frac{d\sigma}{d\Omega}\Phi d\Omega= \frac{d\sigma}{d\Omega}\Phi\ t_{run}\ \sin \theta\ d\theta\ d\phi</math></center> |
| | + | |
| | + | |
| | + | |
| | + | Since the differential cross section is known in the Center of Mass frame of reference, but measurements are taken in the Lab Frame, a transformation must occur. |
| | + | |
| | + | <center><math>\rightarrow dN_{scattered}= \frac{d\sigma}{d\Omega_{Lab}}\Phi\ t\ \sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}</math></center> |
| | + | |
| | + | |
| | + | |
| | + | <center><math>\frac{d\sigma}{d\Omega_{Lab}}\sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}=\frac{d\sigma}{d\Omega_{CM}}\sin \theta_{CM}\ d\theta_{CM}\ d\phi_{CM}</math></center> |
| | + | |
| | + | |
| | + | |
| | + | <center><math>\frac{d\sigma}{d\Omega_{Lab}}=\frac{d\sigma}{d\Omega_{CM}}\frac{\sin \theta_{CM}\ d\theta_{CM}\ d\phi_{CM}}{\sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}}</math></center> |
| | + | |
| | + | |
| | + | <center><math>\rightarrow dN_{scattered}=\frac{d\sigma}{d\Omega_{CM}}\frac{\sin \theta_{CM}\ d\theta_{CM}\ d\phi_{CM}}{\sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}}\Phi\ t_{run}\ \sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}</math></center> |
| | + | |
| | + | |
| | + | If we divide both sides by time |
| | + | |
| | + | |
| | + | <center><math>\rightarrow \frac{dN_{scattered}}{t_{run}}=\frac{d\sigma}{d\Omega_{CM}}\frac{\sin \theta_{CM}\ d\theta_{CM}\ d\phi_{CM}}{\sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}}\Phi \sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}</math></center> |
| | + | |
| | + | |
| | + | |
| | + | <center><math>\rightarrow \frac{dN_{scattered}}{t_{run}}=\frac{d\sigma}{d\Omega_{CM}}\frac{\sin \theta_{CM}\ d\theta_{CM}\ d\phi_{CM}}{\sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}}\frac{N_{incident}}{t_{run}} \sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}</math></center> |
| | + | |
| | + | |
| | + | |
| | + | <center><math>\rightarrow \frac{dN_{scattered}}{N_{incident}}=\frac{d\sigma}{d\Omega_{CM}}\sin \theta_{CM}\ d\theta_{CM}\ d\phi_{CM}</math></center> |
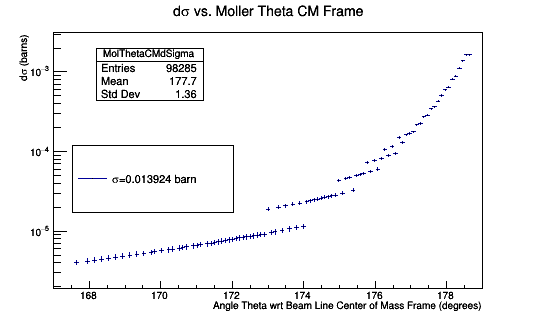
| | Performing a Riemann sum for <math>-30^{\circ} \lt \phi \lt 30^{\circ}</math> | | Performing a Riemann sum for <math>-30^{\circ} \lt \phi \lt 30^{\circ}</math> |
| | | | |
| Line 105: |
Line 154: |
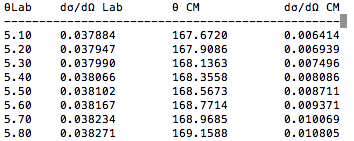
| | ===Bin Spacing of 0.1 degrees for θ in Lab Frame=== | | ===Bin Spacing of 0.1 degrees for θ in Lab Frame=== |
| | | | |
| − | =Using the Cross Section=
| |
| | | | |
| − | If we make the assumption that the beam of incoming electrons is a flux over an area for a given time,
| |
| − |
| |
| − | <center><math>N_{incident}=\Phi\ A_{beam}\ t_{run} \rightarrow dN_{incident}=\Phi\ dA_{beam}\ t_{run}\rightarrow\ \frac{dN_{incident}}{ dA_{beam}}=\Phi\ t_{run}</math></center>
| |
| − |
| |
| − |
| |
| − | Using the definition of the differential cross section:
| |
| − |
| |
| − | <center><math>\frac{d\sigma}{d\Omega}\equiv \frac{ \Biggl(\frac{dN_{scattered}}{d\Omega} \Biggr)}{\Biggl(\frac{dN_{incident}}{dA}\Biggr)}\rightarrow \frac{d\sigma}{d\Omega}\Biggl(\frac{dN_{incident}}{dA}\Biggr)=\Biggl(\frac{dN_{scattered}}{d\Omega} \Biggr)</math></center>
| |
| − |
| |
| − |
| |
| − | Substituting using the flux
| |
| − |
| |
| − | <center><math> \frac{d\sigma}{d\Omega}\Biggl(\frac{dN_{incident}}{dA}\Biggr)=\Biggl(\frac{dN_{scattered}}{d\Omega} \Biggr)\rightarrow \frac{d\sigma}{d\Omega}\Phi\ t_{run}=\Biggl(\frac{dN_{scattered}}{d\Omega} \Biggr)</math></center>
| |
| − |
| |
| − |
| |
| − | <center><math>\rightarrow dN_{scattered}= \frac{d\sigma}{d\Omega}\Phi d\Omega= \frac{d\sigma}{d\Omega}\Phi\ t_{run}\ \sin \theta\ d\theta\ d\phi</math></center>
| |
| − |
| |
| − |
| |
| − |
| |
| − | Since the differential cross section is known in the Center of Mass frame of reference, but measurements are taken in the Lab Frame, a transformation must occur.
| |
| − |
| |
| − | <center><math>\rightarrow dN_{scattered}= \frac{d\sigma}{d\Omega_{Lab}}\Phi\ t\ \sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}</math></center>
| |
| − |
| |
| − |
| |
| − |
| |
| − | <center><math>\frac{d\sigma}{d\Omega_{Lab}}\sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}=\frac{d\sigma}{d\Omega_{CM}}\sin \theta_{CM}\ d\theta_{CM}\ d\phi_{CM}</math></center>
| |
| − |
| |
| − |
| |
| − |
| |
| − | <center><math>\frac{d\sigma}{d\Omega_{Lab}}=\frac{d\sigma}{d\Omega_{CM}}\frac{\sin \theta_{CM}\ d\theta_{CM}\ d\phi_{CM}}{\sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}}</math></center>
| |
| − |
| |
| − |
| |
| − | <center><math>\rightarrow dN_{scattered}=\frac{d\sigma}{d\Omega_{CM}}\frac{\sin \theta_{CM}\ d\theta_{CM}\ d\phi_{CM}}{\sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}}\Phi\ t_{run}\ \sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}</math></center>
| |
| − |
| |
| − |
| |
| − | If we divide both sides by time
| |
| − |
| |
| − |
| |
| − | <center><math>\rightarrow \frac{dN_{scattered}}{t_{run}}=\frac{d\sigma}{d\Omega_{CM}}\frac{\sin \theta_{CM}\ d\theta_{CM}\ d\phi_{CM}}{\sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}}\Phi \sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}</math></center>
| |
| − |
| |
| − |
| |
| − |
| |
| − | <center><math>\rightarrow \frac{dN_{scattered}}{t_{run}}=\frac{d\sigma}{d\Omega_{CM}}\frac{\sin \theta_{CM}\ d\theta_{CM}\ d\phi_{CM}}{\sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}}\frac{N_{incident}}{t_{run}} \sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}</math></center>
| |
| − |
| |
| − |
| |
| − |
| |
| − | <center><math>\rightarrow \frac{dN_{scattered}}{N_{incident}}=\frac{d\sigma}{d\Omega_{CM}}\sin \theta_{CM}\ d\theta_{CM}\ d\phi_{CM}</math></center>
| |
| | | | |
| | =Number of Hits on Wires= | | =Number of Hits on Wires= |
[math]\underline{\textbf{Navigation}}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]
A bash script to run the GEMC simulations is created. tcsh scripts to run root2evio on lds2 is called using sshpass. The lds2 scripts use sshfs
The main script on lds3:
BUILD_GEMC_SIMULATION.sh
The 3 scripts on lds2:
first_commands.tcsh
second_commands.tcsh
last_commands.tcsh
LUND File Output
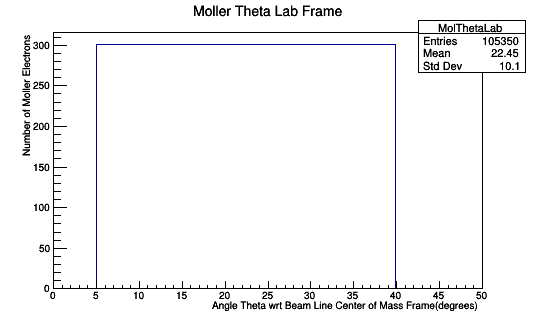
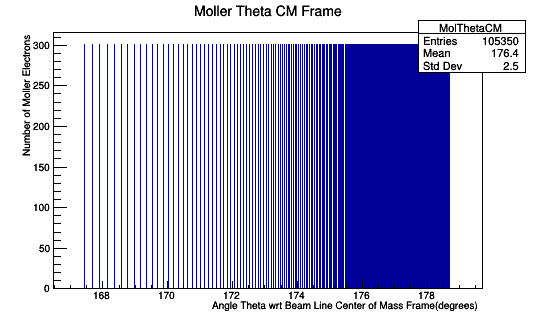
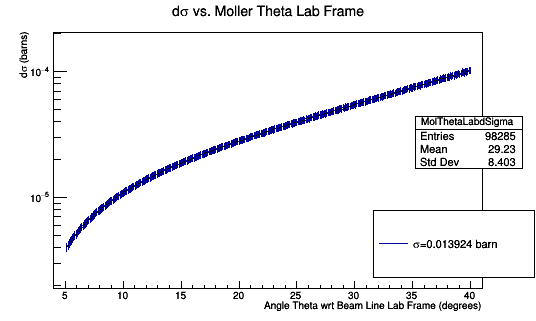
0.1 degree spacing in the Lab frame. CM Frame is not evenly spaced.
Finding the Cross Section
Total cross section over φ

Total cross section over DC limits
If we make the assumption that the beam of incoming electrons is a flux over an area for a given time,
[math]N_{incident}=\Phi\ A_{beam}\ t_{run} \rightarrow dN_{incident}=\Phi\ dA_{beam}\ t_{run}\rightarrow\ \frac{dN_{incident}}{ dA_{beam}}=\Phi\ t_{run}[/math]
Using the definition of the differential cross section:
[math]\frac{d\sigma}{d\Omega}\equiv \frac{ \Biggl(\frac{dN_{scattered}}{d\Omega} \Biggr)}{\Biggl(\frac{dN_{incident}}{dA}\Biggr)}\rightarrow \frac{d\sigma}{d\Omega}\Biggl(\frac{dN_{incident}}{dA}\Biggr)=\Biggl(\frac{dN_{scattered}}{d\Omega} \Biggr)[/math]
Substituting using the flux
[math] \frac{d\sigma}{d\Omega}\Biggl(\frac{dN_{incident}}{dA}\Biggr)=\Biggl(\frac{dN_{scattered}}{d\Omega} \Biggr)\rightarrow \frac{d\sigma}{d\Omega}\Phi\ t_{run}=\Biggl(\frac{dN_{scattered}}{d\Omega} \Biggr)[/math]
[math]\rightarrow dN_{scattered}= \frac{d\sigma}{d\Omega}\Phi d\Omega= \frac{d\sigma}{d\Omega}\Phi\ t_{run}\ \sin \theta\ d\theta\ d\phi[/math]
Since the differential cross section is known in the Center of Mass frame of reference, but measurements are taken in the Lab Frame, a transformation must occur.
[math]\rightarrow dN_{scattered}= \frac{d\sigma}{d\Omega_{Lab}}\Phi\ t\ \sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}[/math]
[math]\frac{d\sigma}{d\Omega_{Lab}}\sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}=\frac{d\sigma}{d\Omega_{CM}}\sin \theta_{CM}\ d\theta_{CM}\ d\phi_{CM}[/math]
[math]\frac{d\sigma}{d\Omega_{Lab}}=\frac{d\sigma}{d\Omega_{CM}}\frac{\sin \theta_{CM}\ d\theta_{CM}\ d\phi_{CM}}{\sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}}[/math]
[math]\rightarrow dN_{scattered}=\frac{d\sigma}{d\Omega_{CM}}\frac{\sin \theta_{CM}\ d\theta_{CM}\ d\phi_{CM}}{\sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}}\Phi\ t_{run}\ \sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}[/math]
If we divide both sides by time
[math]\rightarrow \frac{dN_{scattered}}{t_{run}}=\frac{d\sigma}{d\Omega_{CM}}\frac{\sin \theta_{CM}\ d\theta_{CM}\ d\phi_{CM}}{\sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}}\Phi \sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}[/math]
[math]\rightarrow \frac{dN_{scattered}}{t_{run}}=\frac{d\sigma}{d\Omega_{CM}}\frac{\sin \theta_{CM}\ d\theta_{CM}\ d\phi_{CM}}{\sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}}\frac{N_{incident}}{t_{run}} \sin \theta_{Lab}\ d\theta_{Lab}\ d\phi_{Lab}[/math]
[math]\rightarrow \frac{dN_{scattered}}{N_{incident}}=\frac{d\sigma}{d\Omega_{CM}}\sin \theta_{CM}\ d\theta_{CM}\ d\phi_{CM}[/math]
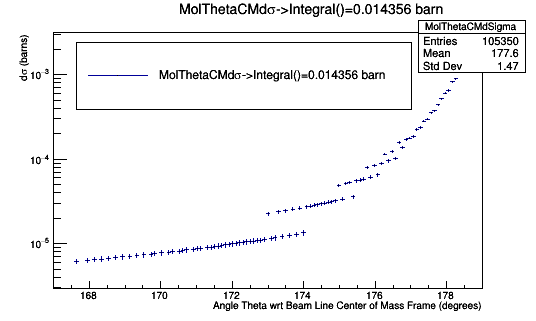
Performing a Riemann sum for [math]-30^{\circ} \lt \phi \lt 30^{\circ}[/math]

The cross section should be equal between both frames since the number of particles is an invariant. The differential cross section must differ between frames since the solid angle does vary.
[math]\sigma_{(CM)}=\sigma{(Lab)}[/math]
[math]\frac{d\sigma}{d\Omega}_{(CM)} d\Omega_{(CM)}=\frac{d\sigma}{d\Omega}_{(Lab)} d\Omega_{(Lab)}[/math]
[math]\frac{d\sigma}{d\Omega}_{(CM)} \sin \theta_{(CM)}\ d\theta_{(CM)}\ d\phi=\frac{d\sigma}{d\Omega}_{(Lab)} \sin \theta_{(Lab)}\ d\theta_{(Lab)}\ d\phi[/math]
[math]\rightarrow \frac{d\sigma}{d\Omega}_{(Lab)}=\frac{d\sigma}{d\Omega}_{(CM)} \frac{\sin \theta_{(CM)}\ d\theta_{(CM)}\ d\phi}{ \sin \theta_{(Lab)}\ d\theta_{(Lab)}\ d\phi}[/math]
[math]\rightarrow d\sigma_{(Lab)}=\frac{d\sigma}{d\Omega}_{(CM)} \frac{\sin \theta_{(CM)}\ d\theta_{(CM)}\ d\phi}{ \sin \theta_{(Lab)}\ d\theta_{(Lab)}\ d\phi}\sin \theta_{(Lab)} d\theta_{(Lab)}\ d\phi[/math]
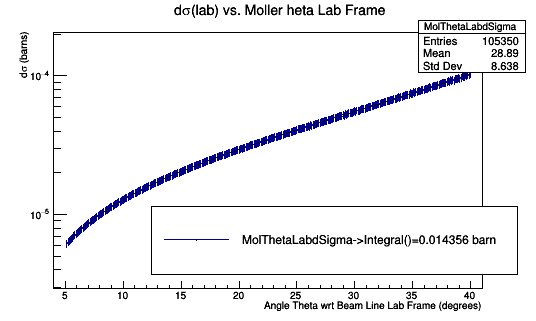

Adjust for DC Sector 1 Limits
GEMC Cross Section
CORRELATED HITS
CORRELATED conditions
| GEMC conditions
|
Meaning
|
| k=0
|
1st registered hit
|
| dpid[k]=11
|
Electron
|
| tid[k]=2
|
Moller electron from LUND file
|
| mpid[k]=0
|
The mother particle implied from LUND file
|
| sector[k]=1
|
Hit is in sector 1
|
Bin Spacing of 0.05 degrees for θ in Lab Frame
Bin Spacing of 0.1 degrees for θ in Lab Frame
Number of Hits on Wires
Not all 1st hits are on layer 1. Using the correlated theoretical wire number associated with the LUND Theta and Phi values:
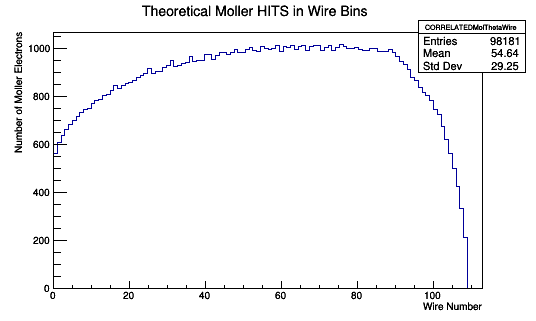
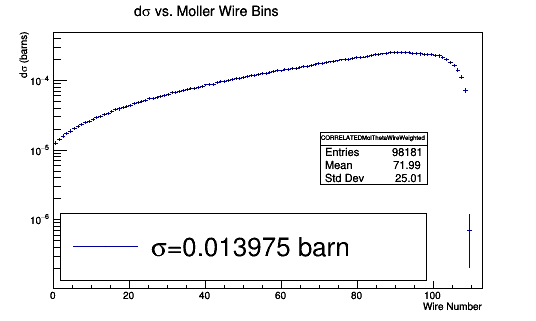
The theoretical model has events which are detected by physically impossible valued wires. If we limit the lowest wire value to 0.5 and the highest to less than 112.5
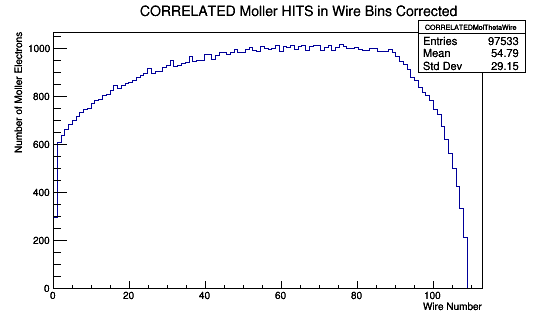
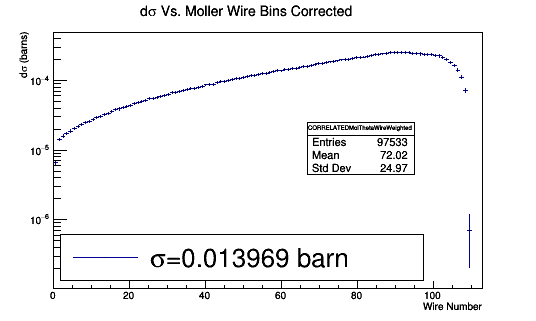
Using the histogram integral function we find the sum of the values for the wire 1 bin. Collecting the individual [math]d\sigma[/math] for each theoretical and physical hits on DC wires.
Occupancy
LH2_NOSol_0Tor_11GeV_IsotropicPhi_v2_6_ShieldOut
Run
./BUILD_GEMC_SIMULATION.sh
DVMacro
Clas12Mon
Create hipo file
Move hipo file to clas12mon folder
mv LH2_NOSol_0Tor_11GeV_IsotropicPhi_v2_6_ShieldOut.hipo ~/clas12mon
Run monitor program
./README
Load hipo file
"Press H for hipo"
"Press play"
"Switch to
For [math]5^{\circ}\gt \theta\lt 40^{\circ}\ -30^{\circ}\gt \phi\lt 30^{\circ}[/math]
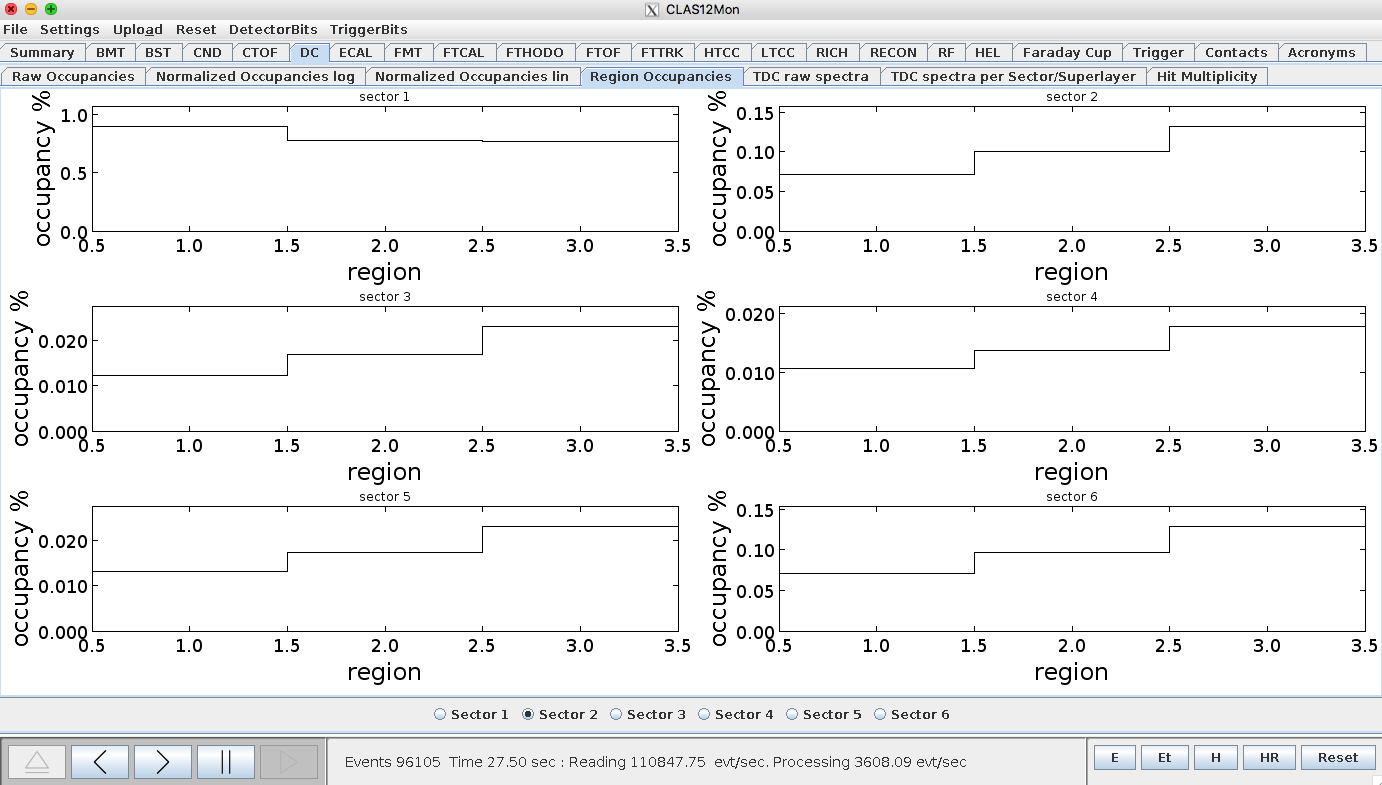
FOR DC Limits
Calculating
[math]N_0=\Delta t \cdot R_{events}=\Delta t \cdot \frac{N_{events}}{t_{simulated}}=250\times 10^{-9}\ s \cdot \frac{98181}{9.3\times 10^{-6}\ s}=2639[/math]
[math]Occupancy=\frac{N_{hits}}{N_0}=\frac{N_{hits}}{\Delta t \cdot R_{events}}=\frac{t_{simulated}\cdot N_{hits}}{N_{events}\cdot \Delta t}=[/math]















