Difference between revisions of "Alpha Ionization"
| (72 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | Alpha particles are highly ionizing and represent the main source for charge in QDC's charge spectrum. Alpha particles are mostly emitted by heavy radioactive nuclei; alpha kinetic energy is dependent on the mass difference before and after emission. For U-233, 85% of alpha particles has energy of 4.82 MeV when U-233 decays to an alpha particle and Th-229.<ref name ="Akovali"> Akovali, Y. (1990, January 1). Table of Radioactive Isotopes. Retrieved January 1, 2014. </ref> | |
| − | + | Performing the simulation for alpha charge passed over specific stages started by using alpha's emission rates. A simulation was benchmarked with published data to determine the amount of primary ionization produced from a single alpha particle for a given energy, the ionization that took place when the primary electrons were accelerated in an external elective field, then the multiplication (gain) by the triple GEM preamplifier structure. And finally, the simulation showed the impact of the shutter on alpha ionization when an FR4 shutter was in front of the U-233 coating. | |
| + | =Alpha emission rates and their energies= | ||
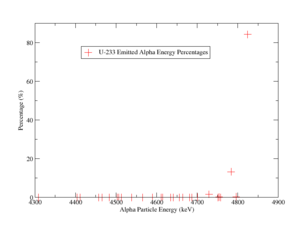
| − | + | Alpha particles has a continuous energy spectrum, which also give relative rates for the emitted alpha. The figure below shows the relative rates for each alpha, | |
| − | + | [[File: alpha_energy_percentages.png | 300 px]] | |
| + | < ref name="Akovali"/> | ||
| + | |||
| + | Alpha particles of an energy of 4.82 MeV has the highest rate of 85 percent compared to the other alpha energies' rates. | ||
| + | |||
| + | The number of alpha and beta particles were measured in the lab <ref> Roy Don</ref>. Before installing U-233 source to be a part of the detector cathode, the number of alpha and beta particles were measured using a standard calibrated drift chamber as shown in the table below, | ||
| − | + | ||
| − | + | {| border="1" celdetectorV"4" | |
| + | |- | ||
| + | | Shutter position || Alpha particles /min.|| Beta particles /min. | ||
| + | |- | ||
| + | | Open || 6879 || 900 | ||
| + | |- | ||
| + | | Close || 1 || 38 | ||
| + | |} | ||
| − | + | The table shows that the shutter almost stopped all alpha and beta particles as it covered the source. Depending on alpha relative intensities, the source rate for emitting 4.82 MeV alpha (most probable) is 97 Hz. | |
| − | + | =An alpha particle's primary and secondary ionization = | |
| − | When an alpha particle travels in | + | The electric field determines the number of primary and secondary electrons in pure argon gas. When an alpha particle travels in pure argon, it liberates up to 30,000 electrons for primary and secondary ionization <ref> Fabio, S. (2014). Basic processes in gaseous counters. In Gaseous Radiation Detectors: Fundamentals and Applications. Cambridge: University Printing House </ref> without any electric field effect. On the other hand, Saito <ref name = "saito"> Saito, K., & Sasaki, S. (2003). Simultaneous Measurements of Absolute Numbers of Electrons and Scintillation Photons Produced by 5.49 MeV Alpha Particles in Rare Gases. IEEE TRANSACTIONS ON NUCLEAR SCIENCE, 50(6), 2452-2460 </ref> measured the number of primary and secondary electrons for a 5.49 MeV alpha particle when a 4.7 kV/cm drift electric field collected the free electrons in the drift area to a collector, the number of collected electrons reached to 200k electron. Saito's measurements shows that the collector almost counts for all electrons, so the electric field decreases the probability of any electron-ion reattachment. |
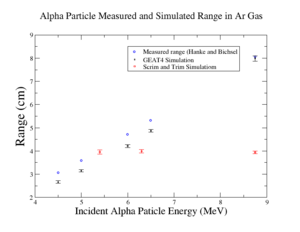
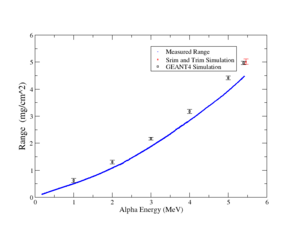
| − | Simulations of GEANT4 <ref> Agostinelli, S. (2003). Geant4—a simulation toolkit. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 506(3), 250–303 </ref> and Srim/Trim <ref>Ziegler, J. (2010). SRIM - The stopping and range of ions in matter (2010). Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 268(11-12), 1818-1823 </ref> were used to estimate the number of primary and secondary electrons for an alpha particle, both of the tools are able to calculate the number of primary and secondary electrons in a specific gaseous medium with | + | Simulations of GEANT4 <ref> Agostinelli, S. (2003). Geant4—a simulation toolkit. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 506(3), 250–303 </ref> and Srim/Trim <ref>Ziegler, J. (2010). SRIM - The stopping and range of ions in matter (2010). Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 268(11-12), 1818-1823 </ref> were used to estimate the number of primary and secondary electrons for an alpha particle, both of the tools are able to calculate the number of primary and secondary electrons in a specific gaseous medium with specific physical conditions for pressure, temperature, and density. The model in each tool was tested by estimating the range in Ar and CO2 gases; the results are shown below: |
| − | [[File:alpha_range_measured_simulated.png | | + | [[File:alpha_range_measured_simulated.png | 300px]] |
| − | [[File:alpha_range_measured_simulated_CO2.png | | + | [[File:alpha_range_measured_simulated_CO2.png | 300px]] |
| − | According to the figures above G4 succeeded to simulate the alpha range accurately in Ar and CO2 | + | According to the figures above, G4 succeeded to simulate the alpha range accurately in Ar and CO2 gases, but the Srim/Trim model estimated the range with 50 percent less than that measured by Hanke and Bichsel <ref> Hanke, C., & Bichsel, H. (1970). Precision energy loss measurements for natural alpha particles in argon. Kbh.: Det Kongelige Danske Videnskabernes Selskab </ref> in pure argon, while on the other hand, Srim/Trim estimated the same range of 4 cm for different alphas' energies in CO2. |
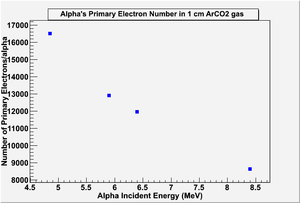
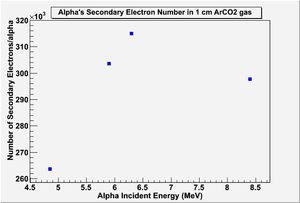
G4 simulated the number of primary and secondary electrons in 1 cm of Ar/CO2 90/10 gas mixture, and the figures below show the results: | G4 simulated the number of primary and secondary electrons in 1 cm of Ar/CO2 90/10 gas mixture, and the figures below show the results: | ||
| Line 29: | Line 42: | ||
[[File:G4_1cmAr90CO2_alpha_primaryElecN.png | 300px]] | [[File:G4_1cmAr90CO2_alpha_primaryElecN.png | 300px]] | ||
[[File:G4_1cmAr90CO2_alpha_SecondElecN.png | 300px]] | [[File:G4_1cmAr90CO2_alpha_SecondElecN.png | 300px]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | G4 estimated 2.7k secondary electrons when a 5.49 MeV alpha penetrated 1cm of the same medium without any applied electric field, the estimation is close to Saito's measurements, which could be interpreted that G4 did not consider the reattachment of the electrons as they were collected in the drift area to end up counting for all the free electrons in the gas. On the other hand, the Scrim and Trim simulation for alpha particles ionizing 1cm of pure Ar gas estimated about 1 MeV deposited energy in the medium within that distance; it made the final number of electrons around 37.5k electron (considering w = 26.7 eV/ip), which is the same estimation mentioned by Sauli. | |
| + | =Triple GEM gain= | ||
| − | + | Garfield, well-known in simulating the interactions in gaseous media such as electron multiplication <ref> Garfield++. (n.d.). Retrieved June 1, 2013. </ref>, simulated the electron multiplication in Ar/CO2 gas in GEM detector. Garfield simulated the physical processes that occurred in triple GEM based detector by using more than one software package simultaneously. Furthermore, Garfield uses HEED and Magboltz that simulate electron interactions in different gases, and give the solution for the Boltzmann equation in 3D. It also uses a finite element method (FEM) package to map the electric field within specific boundary conditions of GEM preamplifiers. | |
| − | + | Garfield simulated a triple GEM detector electron multiplication in more than one region in the detector. When the electric field of 1-4kV/cm drives the electrons toward the first GEM preamplifier in 1cm drift region, electrons interact with the gas atoms and molecules. According to Garfield simulation for the drift region, A 200eV electron multiplies to 8 +_1 electrons before it reaches the first GEM preamplifier. In addition, Garfield simulated the gain for a triple GEM stack for Ar/CO2 93/7 as in figure XX. The figure shows that Garfield estimated almost the same measured gain for triple GEM when voltage difference for each GEM preamplifier is 300V and 320V; however, as the voltage increased to 340V, Garfield overestimated the gain up to 25% more than the measured value. | |
| − | |||
| + | [[File:ref_data_gain_triple_Ar93_CO2.png| 300px ]] | ||
| − | + | =FR4 Shutter Effect= | |
| − | |||
| − | + | Simulations and measurements proved that an FR4 plate almost stops all Alpha particles that are emitted from U-233. An FR4 plate of 1 mm thickness has been used as a shutter to stop alpha and beta particles. Roy's (2012) and different QDC's measurements have shown a difference in the number of counts when the shutter is open, and when it was close covering the whole U-233 coating. The difference proved the shutter ability to stop alpha particles. Also GEANT4 simulated 1 mm FR4 ability to stop alpha particles, and predicted the alpha particle energy that would be able to penetrate the shutter as shown in the figure yy, For a complete penetration, alpha's energy has to be around 55 MeV, as previously stated. the emitted alpha particles from U-233 has a maximum energy of 8.4 MeV and most probable energy of 4.82 MeV, The result indicates that the shutter is able to stop all the emitted alpha particles in the drift region with a minimum ionization shown in QDC spectrum. | |
| − | |||
[[File:G4_alpha_tran_FR4_vacuum.png | 300px]] | [[File:G4_alpha_tran_FR4_vacuum.png | 300px]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[alpha particle simulation related]] | [[alpha particle simulation related]] | ||
Latest revision as of 15:25, 8 April 2015
Alpha particles are highly ionizing and represent the main source for charge in QDC's charge spectrum. Alpha particles are mostly emitted by heavy radioactive nuclei; alpha kinetic energy is dependent on the mass difference before and after emission. For U-233, 85% of alpha particles has energy of 4.82 MeV when U-233 decays to an alpha particle and Th-229.<ref name ="Akovali"> Akovali, Y. (1990, January 1). Table of Radioactive Isotopes. Retrieved January 1, 2014. </ref>
Performing the simulation for alpha charge passed over specific stages started by using alpha's emission rates. A simulation was benchmarked with published data to determine the amount of primary ionization produced from a single alpha particle for a given energy, the ionization that took place when the primary electrons were accelerated in an external elective field, then the multiplication (gain) by the triple GEM preamplifier structure. And finally, the simulation showed the impact of the shutter on alpha ionization when an FR4 shutter was in front of the U-233 coating.
Alpha emission rates and their energies
Alpha particles has a continuous energy spectrum, which also give relative rates for the emitted alpha. The figure below shows the relative rates for each alpha,
Alpha particles of an energy of 4.82 MeV has the highest rate of 85 percent compared to the other alpha energies' rates.
The number of alpha and beta particles were measured in the lab <ref> Roy Don</ref>. Before installing U-233 source to be a part of the detector cathode, the number of alpha and beta particles were measured using a standard calibrated drift chamber as shown in the table below,
| Shutter position | Alpha particles /min. | Beta particles /min. |
| Open | 6879 | 900 |
| Close | 1 | 38 |
The table shows that the shutter almost stopped all alpha and beta particles as it covered the source. Depending on alpha relative intensities, the source rate for emitting 4.82 MeV alpha (most probable) is 97 Hz.
An alpha particle's primary and secondary ionization
The electric field determines the number of primary and secondary electrons in pure argon gas. When an alpha particle travels in pure argon, it liberates up to 30,000 electrons for primary and secondary ionization <ref> Fabio, S. (2014). Basic processes in gaseous counters. In Gaseous Radiation Detectors: Fundamentals and Applications. Cambridge: University Printing House </ref> without any electric field effect. On the other hand, Saito <ref name = "saito"> Saito, K., & Sasaki, S. (2003). Simultaneous Measurements of Absolute Numbers of Electrons and Scintillation Photons Produced by 5.49 MeV Alpha Particles in Rare Gases. IEEE TRANSACTIONS ON NUCLEAR SCIENCE, 50(6), 2452-2460 </ref> measured the number of primary and secondary electrons for a 5.49 MeV alpha particle when a 4.7 kV/cm drift electric field collected the free electrons in the drift area to a collector, the number of collected electrons reached to 200k electron. Saito's measurements shows that the collector almost counts for all electrons, so the electric field decreases the probability of any electron-ion reattachment.
Simulations of GEANT4 <ref> Agostinelli, S. (2003). Geant4—a simulation toolkit. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 506(3), 250–303 </ref> and Srim/Trim <ref>Ziegler, J. (2010). SRIM - The stopping and range of ions in matter (2010). Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 268(11-12), 1818-1823 </ref> were used to estimate the number of primary and secondary electrons for an alpha particle, both of the tools are able to calculate the number of primary and secondary electrons in a specific gaseous medium with specific physical conditions for pressure, temperature, and density. The model in each tool was tested by estimating the range in Ar and CO2 gases; the results are shown below:
According to the figures above, G4 succeeded to simulate the alpha range accurately in Ar and CO2 gases, but the Srim/Trim model estimated the range with 50 percent less than that measured by Hanke and Bichsel <ref> Hanke, C., & Bichsel, H. (1970). Precision energy loss measurements for natural alpha particles in argon. Kbh.: Det Kongelige Danske Videnskabernes Selskab </ref> in pure argon, while on the other hand, Srim/Trim estimated the same range of 4 cm for different alphas' energies in CO2.
G4 simulated the number of primary and secondary electrons in 1 cm of Ar/CO2 90/10 gas mixture, and the figures below show the results:
G4 estimated 2.7k secondary electrons when a 5.49 MeV alpha penetrated 1cm of the same medium without any applied electric field, the estimation is close to Saito's measurements, which could be interpreted that G4 did not consider the reattachment of the electrons as they were collected in the drift area to end up counting for all the free electrons in the gas. On the other hand, the Scrim and Trim simulation for alpha particles ionizing 1cm of pure Ar gas estimated about 1 MeV deposited energy in the medium within that distance; it made the final number of electrons around 37.5k electron (considering w = 26.7 eV/ip), which is the same estimation mentioned by Sauli.
Triple GEM gain
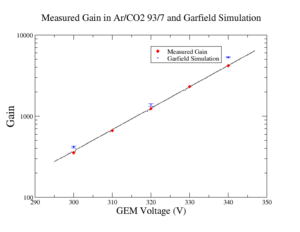
Garfield, well-known in simulating the interactions in gaseous media such as electron multiplication <ref> Garfield++. (n.d.). Retrieved June 1, 2013. </ref>, simulated the electron multiplication in Ar/CO2 gas in GEM detector. Garfield simulated the physical processes that occurred in triple GEM based detector by using more than one software package simultaneously. Furthermore, Garfield uses HEED and Magboltz that simulate electron interactions in different gases, and give the solution for the Boltzmann equation in 3D. It also uses a finite element method (FEM) package to map the electric field within specific boundary conditions of GEM preamplifiers.
Garfield simulated a triple GEM detector electron multiplication in more than one region in the detector. When the electric field of 1-4kV/cm drives the electrons toward the first GEM preamplifier in 1cm drift region, electrons interact with the gas atoms and molecules. According to Garfield simulation for the drift region, A 200eV electron multiplies to 8 +_1 electrons before it reaches the first GEM preamplifier. In addition, Garfield simulated the gain for a triple GEM stack for Ar/CO2 93/7 as in figure XX. The figure shows that Garfield estimated almost the same measured gain for triple GEM when voltage difference for each GEM preamplifier is 300V and 320V; however, as the voltage increased to 340V, Garfield overestimated the gain up to 25% more than the measured value.
FR4 Shutter Effect
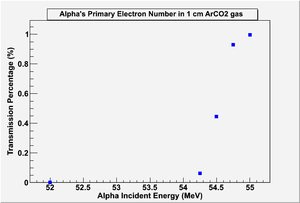
Simulations and measurements proved that an FR4 plate almost stops all Alpha particles that are emitted from U-233. An FR4 plate of 1 mm thickness has been used as a shutter to stop alpha and beta particles. Roy's (2012) and different QDC's measurements have shown a difference in the number of counts when the shutter is open, and when it was close covering the whole U-233 coating. The difference proved the shutter ability to stop alpha particles. Also GEANT4 simulated 1 mm FR4 ability to stop alpha particles, and predicted the alpha particle energy that would be able to penetrate the shutter as shown in the figure yy, For a complete penetration, alpha's energy has to be around 55 MeV, as previously stated. the emitted alpha particles from U-233 has a maximum energy of 8.4 MeV and most probable energy of 4.82 MeV, The result indicates that the shutter is able to stop all the emitted alpha particles in the drift region with a minimum ionization shown in QDC spectrum.
alpha particle simulation related
<References/>
GO BACK [1]