Difference between revisions of "TF EIM Chapt6"
| (27 intermediate revisions by the same user not shown) | |||
| Line 7: | Line 7: | ||
*higher input impedance than bi-polar | *higher input impedance than bi-polar | ||
*less gain than bi-polar | *less gain than bi-polar | ||
| − | + | *better temperature stability | |
=JFET = | =JFET = | ||
| Line 84: | Line 84: | ||
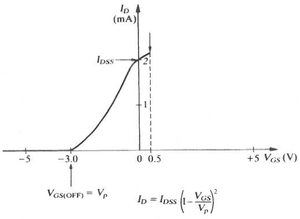
| − | <math>I_{DSS} \equiv</math> Maximum drain current (current flows from Drain to Source with the gate Shorted; ie <math>V_{GS}</math> = 0) | + | You can find the "pinchoff" voltage by making V_{GS} more negative (n-channel) until the drain current I_D becomes zero. |
| + | |||
| + | |||
| + | In the other extreme | ||
| + | |||
| + | :<math>I_{DSS} \equiv</math> Maximum drain current (current flows from Drain to Source with the gate Shorted; ie <math>V_{GS}</math> = 0) | ||
| + | |||
| + | ==Temperature== | ||
| + | |||
| + | Because of the way a JFET operates, by pinching the current, the device heats up less at higher currents because you are no longer restricting the current flow. | ||
| + | |||
| + | At low values of<math> I_D</math> and increase in the device temperature will cause an increase in <math>I_D</math>. | ||
| + | |||
| + | But at high values of <math>I_D</math> the increase in temperature decreases <math>I_D</math>. | ||
| + | |||
| + | This feature of the JFET allows you to chain several together for amplification such that if one starts to overheat it will amplify less. | ||
| + | |||
| + | == Characteristic curve== | ||
| + | |||
| + | The JFET has a characteristic curve that is similar to the bi-polar transistor. In the case of the bi-polar transistor you saw a dependence of the collector current (<math>I_C</math>) on the potential difference between the collector and the emitter (<math>V_{CE}</math>) for several values of the base current <math>I_B.</math> | ||
| + | |||
| + | The JFET has a similar characteristic curve which the drain current (<math>I_D</math>) depends on the voltage difference between the drain and source (<math>V_{DS}</math>) for several values of the gate-source potential difference (<math>V_{S}</math>). | ||
| + | |||
| + | The difference is that higher base current in the bi-polar transistor yields higher output currents whereas in the JFET you get higher output currents with the least negative gate bias (n-channel). | ||
| + | |||
| + | |||
| + | [[File:TF_EIM_JFET_Vgs-vs-Id.png | 300 px]][[File:TF_EIM_JFET_Vds-vs-Id.png | 300 px]] | ||
| + | |||
| + | = Equivalent circuit= | ||
| + | |||
| + | The method of Equivalent circuits seeks to describe the performance of a circuit in terms of it input and output voltages and currents. One you know the dependence of these parameters then the circuit becomes a black box. | ||
| + | |||
| + | |||
| + | |||
| + | Let | ||
| + | |||
| + | <math>V_{in}, V_{out}, I_{in}, I_{out}</math> be the four variables which describe the circuit. | ||
| + | |||
| + | choose | ||
| + | |||
| + | <math>V_{in}</math> and <math>V_{out}</math> as the independent variables which will be described by the dependent variables <math>I_{in}</math> and <math>I_{out}</math> | ||
| + | |||
| + | In other words you express the currents as functions of the voltages | ||
| + | |||
| + | :<math>I_{in} = f_{in}(V_{in},V_{out})</math> | ||
| + | :<math>I_{in} = f_{out}(V_{in},V_{out})</math> | ||
| + | |||
| + | |||
| + | using the chain rule you can express small changes in the current as | ||
| + | |||
| + | :<math>\Delta I_{in} = \left ( \frac{\partial I_{in}}{\partial V_{in}} \right ) \Delta V_{in} + \left ( \frac{\partial I_{in}}{\partial V_{out}} \right ) \Delta V_{out}</math> | ||
| + | :<math>\Delta I_{out} = \left ( \frac{\partial I_{out}}{\partial V_{in}} \right ) \Delta V_{in} + \left ( \frac{\partial I_{out}}{\partial V_{out}} \right ) \Delta V_{out}</math> | ||
| + | |||
| + | ;Note:The derivatives with respect to one voltage are taken for fixed values of the other voltage. | ||
| + | |||
| + | |||
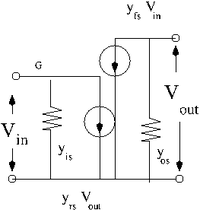
| + | You define the derivative in terms of "y-parameters" such that | ||
| + | |||
| + | :<math>y_{is} \equiv \left ( \frac{\partial I_{in}}{\partial V_{in}} \right )</math> = input conductance | ||
| + | |||
| + | : <math>y_{rs} \equiv \left ( \frac{\partial I_{in}}{\partial V_{out}} \right )</math> | ||
| + | |||
| + | : <math>y_{fs} \equiv \left ( \frac{\partial I_{out}}{\partial V_{in}} \right )</math> | ||
| + | |||
| + | : <math>g_m \equiv y_{os} \equiv \left ( \frac{\partial I_{out}}{\partial V_{out}} \right )</math> = output conductance | ||
| + | |||
| + | |||
| + | In the case of the common source JFET configuration | ||
| + | |||
| + | <math>I_{in} = I_G</math> , <math>I_{out} = I_D</math> | ||
| + | |||
| + | ==admittance== | ||
| + | |||
| + | ;Notice: The above y-parameters have units of inverse Ohms | ||
| + | |||
| + | The SI unit for this is called the "siemens" and is represented by '''S''' | ||
| + | |||
| + | :<math>\mbox {siemens} = S = \frac{1}{\mbox {Ohms}} = \Omega^{-1}</math> | ||
| + | |||
| + | The inverse of resistance is conductance. | ||
| + | |||
| + | In electric engineering the term "admittance" is used to describe how easily a circuit will allow current to flow (its conductance). | ||
| + | |||
| + | The unit "mho" is also used as an equivalent unit to '''S''' used by electrical engineers. | ||
| + | |||
| + | |||
| + | :<math>\mbox {mho} = \frac{1}{\mbox {Ohms}} = \Omega^{-1}</math> | ||
| + | |||
| + | |||
| + | == the JFET equivalent Circuit== | ||
| + | |||
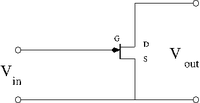
| + | Below is a common source JFET configuration. The Gate and Drain have the Source line as a common reference. This is analogous to the common emitter configuration discussed in the last chapter and using in [[Lab_14_TF_EIM]]. | ||
| + | |||
| + | [[File:TF_EIM_JFET_CommonSOurceCircuit.png| 200 px]] | ||
| + | |||
| + | |||
| + | ===DC=== | ||
| + | |||
| + | [[File:TF_EIM_JFET_DCequivCircuit.png| 200 px]] | ||
| + | |||
| + | |||
| + | The arrows with circles indicate ideal current sources. The one on the left has the current <math>y_{rs}V_{out}</math> and the one on the right <math>y_{rs}V_{in}</math> | ||
| + | |||
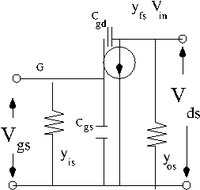
| + | ===AC=== | ||
| + | [[File:TF_EIM_JFET_ACequivCircuit.png| 200 px]] | ||
| + | |||
| + | C_{gs} is the capacitance between the gate and the source. | ||
| + | |||
| + | C_{gd} is the capacitance between the gate and the drain. | ||
=MOSFET= | =MOSFET= | ||
Latest revision as of 15:00, 6 April 2011
Field Effect Transistors (FET, JFET, MOSFET)
Properties
FETs differ from the bipolar transistors in the las chapter in that the current from a FET is only due to the majority charge carriers in the semiconductor while bi-polar transistors current is produced from both carrier types; electron and hole.
- higher input impedance than bi-polar
- less gain than bi-polar
- better temperature stability
JFET
JFET Junction Field Effect Transistor
In a bi-polar transistor you have a depletion region with mixed charge carriers
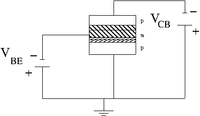 |
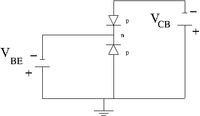 |
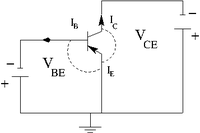
|
| pnp bi-polar transistor | Equivalence circuit | Circuit diagram |
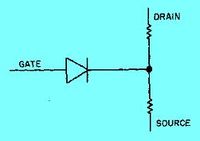
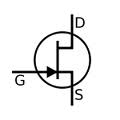
In the Junction Field Effect Transistor you have a single charge carrier with the minority charge carriers forming a choke point for the majority carrier current flow. It is similar to "pinching" a garden hose when water is flowing through it.
 |
 |
|
| JFET | Equivalence circuit | Circuit diagram |
The semiconductor material of the gate is the opposite of the channel. Here the n-p (or p-n) junction is between the gate and the channel.
The JFET operates by reverse biasing the gate-channel junction (diode) so the gate current doesn't flow in the direction indicated by the circuit diagram symbol. This means that the current through the gate is small (nAmps). As a result the input impedance looking into the gate is high (M) for the equivalent circuit.
The current junction rule is
for the Bi-Polar transistor
Resistance
The FET acts like a resistor.
Consider the following circuit
Let
the drain driving voltage
= resistor between the drain and V_{DD}
if = resistivity of the n-type semiconductor
then
- r = = resistance of the JFET
If you reverse bias the gate then the depletion region at the p-n junction expands into the n-type material thereby reducing the cross-sectional area (A) of the channel.
FET pinchoff
If you continue to reverse bias the gate, keeping V_{DD} constant, then the drain current will decrease as you make the gate more negative.
The pinchoff condition will occur when the reverse bias is large enough to stop the drain current I_D.
where
- = dielectric constant
- = thickness of the channel
- = number of impurity atoms per volume
You can find the "pinchoff" voltage by making V_{GS} more negative (n-channel) until the drain current I_D becomes zero.
In the other extreme
- Maximum drain current (current flows from Drain to Source with the gate Shorted; ie = 0)
Temperature
Because of the way a JFET operates, by pinching the current, the device heats up less at higher currents because you are no longer restricting the current flow.
At low values of and increase in the device temperature will cause an increase in .
But at high values of the increase in temperature decreases .
This feature of the JFET allows you to chain several together for amplification such that if one starts to overheat it will amplify less.
Characteristic curve
The JFET has a characteristic curve that is similar to the bi-polar transistor. In the case of the bi-polar transistor you saw a dependence of the collector current () on the potential difference between the collector and the emitter () for several values of the base current
The JFET has a similar characteristic curve which the drain current () depends on the voltage difference between the drain and source () for several values of the gate-source potential difference ().
The difference is that higher base current in the bi-polar transistor yields higher output currents whereas in the JFET you get higher output currents with the least negative gate bias (n-channel).
Equivalent circuit
The method of Equivalent circuits seeks to describe the performance of a circuit in terms of it input and output voltages and currents. One you know the dependence of these parameters then the circuit becomes a black box.
Let
be the four variables which describe the circuit.
choose
and as the independent variables which will be described by the dependent variables and
In other words you express the currents as functions of the voltages
using the chain rule you can express small changes in the current as
- Note
- The derivatives with respect to one voltage are taken for fixed values of the other voltage.
You define the derivative in terms of "y-parameters" such that
- = input conductance
- = output conductance
In the case of the common source JFET configuration
,
admittance
- Notice
- The above y-parameters have units of inverse Ohms
The SI unit for this is called the "siemens" and is represented by S
The inverse of resistance is conductance.
In electric engineering the term "admittance" is used to describe how easily a circuit will allow current to flow (its conductance).
The unit "mho" is also used as an equivalent unit to S used by electrical engineers.
the JFET equivalent Circuit
Below is a common source JFET configuration. The Gate and Drain have the Source line as a common reference. This is analogous to the common emitter configuration discussed in the last chapter and using in Lab_14_TF_EIM.
DC
The arrows with circles indicate ideal current sources. The one on the left has the current and the one on the right
AC
C_{gs} is the capacitance between the gate and the source.
C_{gd} is the capacitance between the gate and the drain.
MOSFET
MOSFET Metal-Oxide-Semiconductor Field Effect Transistor