Difference between revisions of "Emittance Test"

From New IAC Wiki
Jump to navigation Jump to search
 
(58 intermediate revisions by 2 users not shown)
Line 16: Line 16:
  
 
[[File:Emittance_Desien_27th_Jul_2010.png | 300 px]]
 
[[File:Emittance_Desien_27th_Jul_2010.png | 300 px]]
 +
 +
[[File:HRRL_Emittance_Desien_27th_Jul_2010.png | 300 px]]
  
 
Optim File on 27th, Jul. 2010:
 
Optim File on 27th, Jul. 2010:
Line 25: Line 27:
  
 
[[File:HRRL_Emittance.pdf]]
 
[[File:HRRL_Emittance.pdf]]
 +
 +
== YAG (Yttrium Aluminum Garnet) Christal ==
 +
 +
[[File:YAG_Christal_for_HRRL_2010_July_Emittance_Test.jpg | 300 px]]
 +
  
 
==Faraday Cup==
 
==Faraday Cup==
Line 51: Line 58:
 
[[File:Beam_Line_Parts_HRRL_Positorns_2.jpg | 300 px]]
 
[[File:Beam_Line_Parts_HRRL_Positorns_2.jpg | 300 px]]
 
[[File:Beam_Line_Parts_HRRL_Positorns_3.jpg | 300 px]]
 
[[File:Beam_Line_Parts_HRRL_Positorns_3.jpg | 300 px]]
−
[[File:Beam_Line_Parts_HRRL_Positorns_4.jpg | 300 px]]
 
−
[[File:Beam_Line_Parts_HRRL_Positorns_5.jpg | 300 px]]
 
 
[[File:Beam_Line_Parts_HRRL_Positorns_6.jpg | 300 px]]
 
[[File:Beam_Line_Parts_HRRL_Positorns_6.jpg | 300 px]]
 
[[File:Beam_Line_Parts_HRRL_Positorns_7.jpg | 300 px]]
 
[[File:Beam_Line_Parts_HRRL_Positorns_7.jpg | 300 px]]
Line 60: Line 65:
 
[[File:Beam_Line_Parts_HRRL_Positorns_11.jpg | 300 px]]
 
[[File:Beam_Line_Parts_HRRL_Positorns_11.jpg | 300 px]]
 
[[File:Beam_Line_Parts_HRRL_Positorns_12.jpg | 300 px]]
 
[[File:Beam_Line_Parts_HRRL_Positorns_12.jpg | 300 px]]
 +
 +
 +
Length of the pole face of Quad2Tin z direction is 8 cm.
 +
 +
[[File:Beam_Line_Parts_HRRL_Positorns_4.jpg | 300 px]]
 +
[[File:Beam_Line_Parts_HRRL_Positorns_5.jpg | 200 px]]
  
 
==Constructed Beam Line for Emittance Test ==
 
==Constructed Beam Line for Emittance Test ==
Line 1,079: Line 1,090:
 
|-
 
|-
 
|    || <math> 90.29 \pm 0.49 </math> ||  <math> 59.43 \pm 0.53 </math> ||   
 
|    || <math> 90.29 \pm 0.49 </math> ||  <math> 59.43 \pm 0.53 </math> ||   
−
|-
 
−
|    ||  Horizontal pixels/mm  ||  Vertical pixels/mm || 
 
−
|-
 
−
|    || <math> 9.029 \pm 0.049 </math> ||  <math> 5.943 \pm 0.053 </math> || 
 
 
|-
 
|-
 
|    ||  Horizontal mm/pixels  ||  Vertical mm/pixels ||   
 
|    ||  Horizontal mm/pixels  ||  Vertical mm/pixels ||   
 
|-
 
|-
−
|    || <math> 0.1108 \pm 0.0006 </math> ||  <math> 0.1683 \pm 0.0015 </math> ||
+
|    || <math> 0.1108 \pm 0.0006 </math> ||  <math> 0.1683 \pm 0.0015 </math> ||  
 
|-
 
|-
 
|}
 
|}
Line 1,187: Line 1,194:
 
==  Emittance  ==
 
==  Emittance  ==
  
−
Quadrupole Strength: <math>  k = 0.2998  \frac{g[T/m]}{GeV}  </math>
+
Quadrupole Strength: <math>  k = 0.2998  \frac{g[T/m]}{p[GeV]}  </math>
  
−
g here is the gradient of the qudrupole.
+
g here is the gradient of the qudrupole. p is the momentum of the e- beam.
  
 
In our case, energy of the beam is 0.01 GeV and gap between dipole center and pole face is 1 inch.
 
In our case, energy of the beam is 0.01 GeV and gap between dipole center and pole face is 1 inch.
Line 1,232: Line 1,239:
 
If I have a fit:
 
If I have a fit:
  
−
<math> \sigma_{screen11} = sk^2 + yk + z </math>
+
<math> \sigma_{screen11} = xk^2 + yk + z </math>
  
 
Then, <math> A=x, B=\frac{y}{-2A}, C=z-AB^2</math>
 
Then, <math> A=x, B=\frac{y}{-2A}, C=z-AB^2</math>
Line 1,325: Line 1,332:
  
 
=Automatic Script to plot RMS=
 
=Automatic Script to plot RMS=
 +
 +
== ROOT ==
  
 
  How does the fit look when using the script below.
 
  How does the fit look when using the script below.
Line 1,343: Line 1,352:
  
 
This 2 programs and pictures for data can be downloaded at: [http://inca.iac.isu.edu/~setiniyaz/All_Scan.tar.gz]
 
This 2 programs and pictures for data can be downloaded at: [http://inca.iac.isu.edu/~setiniyaz/All_Scan.tar.gz]
 +
 +
==  MATLAB ==
 +
 +
These MATLAB scripts will do Gaussian fits for beam spots and get rms beam size on x and projections (by Gauss_Fit.m). These rms values will be passed on (to Emit_Parabola_Fit_kl_YProjection.m and Emit_Parabola_Fit_kl_YProjection.m) to fit parabola. Parabola fit will be plotted,and emittances, normalized emittances, beta functions, alpha functions will given at the end.
 +
 +
[[File:Get_Emittance.rar]]
 +
 +
[[File:Guass_Fit.txt]]
 +
 +
[[File:Emit_Parabola_Fit_kl_XProjection.txt]]
 +
 +
[[File:Emit_Parabola_Fit_kl_YProjection.txt]]
 +
 +
[[File:gauss.txt]]
 +
 +
[[File:gausschisq.txt]]
 +
 +
[[File:gaussfit.txt]]
 +
 +
[[File:Plot_Beam_Spot.txt]]
 +
 +
[[File:Plot_Gauss_Fit.txt]]
 +
 +
[[File:ReadMe.txt]]
 +
 +
=Alternative Analysis from the East Cost=
 +
 +
[[Image Analysis]]
 +
 +
[[Emittance/TWISS parameter extraction]]
 +
 +
 +
=New Fits with K1L=
 +
 +
== No Fringe Field Effect ==
 +
 +
We want to do new fits with K1L. K1 is quadrupole strength and L is the thickness of the quadrupole. We will do it for the data we got previously. They are the following two data sets.
 +
 +
'''At this step, we will ignore fringe field effect, we want to consider it later.'''
 +
 +
 +
need uncertainties in plots below
 +
 +
The uncertainties are difficult to believe because they are so small (< 0.1% !)
 +
 +
Redo you plots so they look like the ones below in terms of line boldness and quality.  Identify the fit parameters and their error as well as a measurement of the goodness of fit.
 +
 +
https://wiki.iac.isu.edu/index.php/File:Emittance_HRRL_1mA.png
 +
 +
 +
 +
Data files contains:
 +
 +
Number-of-points  B-Field-Strength  Error-on-B-Field-Strength  Sigma^2 Error-on-Sigma^2
 +
 +
 +
 +
[[File:HRRL_Emit_Parbola_Fit_Xaxis_as_BfieldStrength.txt]]
 +
 +
[[File:HRRL_Emit_Parbola_Fit_Yaxis_as_BfieldStrength.txt]]
 +
 +
X-Projection:
 +
Fit Parameters by MATLAB:
 +
y = 0.00000784 + (0.00000288)*x + 0.00000031*x*x
 +
Fit Parameters by Matrix Inversion:
 +
y = (0.00000781+-0.00000027) + (0.00000282+-0.00000014)*x + (0.00000030+-0.00000002)*x*x
 +
P-value = 7.6238e-21
 +
 +
Y-Projection:
 +
Fit Parameters by MATLAB:
 +
y = 0.00001766 + (-0.00000599)*x + 0.00000066*x*x
 +
Fit Parameters by Matrix Inversion:
 +
y = (0.00001717+-0.00000084) + (-0.00000558+-0.00000041)*x + (0.00000059+-0.00000005)*x*x
 +
P-value =  0.020964
 +
 +
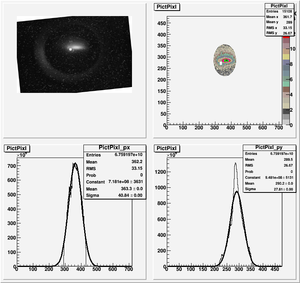
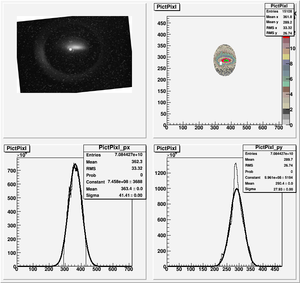
geometrical emittance:    <math>\epsilon_{x}  =  1.5  \pm  1.4  ~ mm*mrad</math>    <math>\epsilon_{y} =  3.7 \pm 3.9  ~ mm*mrad </math>
 +
normalized emittance:    <math>\epsilon_{n,x}  =  29    \pm  27 ~ mm*mrad</math>    <math>\epsilon_{n,y} = 72.0 \pm  77.0 ~ mm*mrad </math>
 +
                          <math>\beta_{x} = 0.49  \pm 0.23  </math>                    <math>\beta_{y} = 0.39 \pm 0.16  </math>
 +
                          <math>\alpha_{x} = -1.53  \pm  0.72 </math>                <math>\alpha_{y} = 2.5  \pm 1.0 </math>
 +
 +
 +
 +
 +
 +
 +
X Projection:
 +
 +
[[File:HRRL_Emit_New_Fits_with_K1L_X_Projection_withErr.png | 400 px]]
 +
 +
 +
Y Projection:
 +
 +
[[File:HRRL_Emit_New_Fits_with_K1L_Y_Projection_withErr.png | 400 px]]
 +
 +
 +
 +
 +
 +
 +
 +
 +
= Corrections for vertical calibration =
 +
 +
We made error when we are doing vertical calibration. When we calculate vertical calibration, we need to multiply the diameter of the circle by <math> cos45^{o} </math>.
 +
 +
This is the reason that we got dramatically different results in vertical and horizontal emittances.
 +
 +
 +
 +
== Errors in Converting pixels to length for Vertical  ==
 +
 +
 +
{| border="1"  |cellpadding="20" cellspacing="0
 +
|-
 +
|    ||  Average Horizontal Diameter (pixels)  ||  Average Vertical Diameter (pixels)  || 
 +
|-
 +
|    || <math> 90.29 \pm 0.49 </math> ||  <math> 59.43 \pm 0.53 </math> || 
 +
|-
 +
|    ||  Horizontal mm/pixels  ||  Vertical mm/pixels || 
 +
|-
 +
|    || <math> 0.1108 \pm 0.0006 </math> ||  <math> 0.1683 \pm 0.0015 </math> || 
 +
|-
 +
|    || || <math> V_{cal} </math> need to be multiplied by <math> cos45^{o} </math>  || 
 +
|-
 +
|    || ||  <math> 0.1190\pm 0.0011 </math>  || 
 +
|-
 +
|}
 +
 +
== New Fits with K1L ==
 +
 +
=== Considering fringe field effect with "Cheap and Dirty" way===
 +
 +
==== X Projection ====
 +
 +
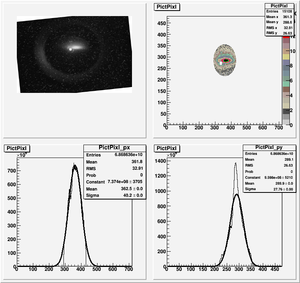
[[File:HRRL_Emitt_2010_Jul_Refit_After_Correcting_Calibration_Projection_X.png | 300 px]]
 +
 +
x-projection:
 +
 +
emit=2.2 +- 1.3 mm*mrad, emit_norm=42.4 +- 25.4 mm*mrad
 +
 +
beta=0.72 +- 0.31, alpha=-1.23 +-0.56
 +
 +
//K1*L(1/m)  er K1*L    sgima^2(mm)  er sigma^2
 +
 +
[[Media:2010_Jul_Emit_refit_data_x.txt]]
 +
 +
 +
parabola fit for x-projection (y in mm unit):
 +
 +
y = (8.05126 +-0.24983) + (4.18341+-0.18968)*x + (0.64143+-0.03472)*x.*x
 +
 +
Data created from parabola fit
 +
 +
[[Media:2010_Jul_Emit_data_from_fit_x.txt]]
 +
 +
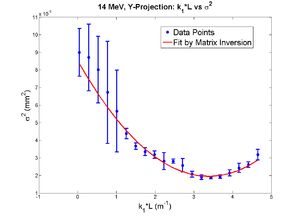
==== Y Projection ====
 +
 +
 +
 +
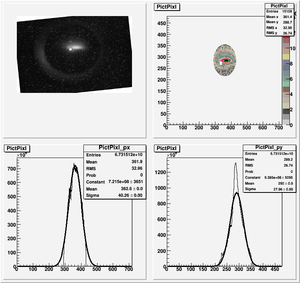
[[File:HRRL_Emitt_2010_Jul_Refit_After_Correcting_Calibration_Projection_Y.png | 300 px]]
 +
 +
 +
y-projection:
 +
 +
emit=2.6 +- 2.0 mm*mrad, emit_norm=50.5 +- 38.3 mm*mrad
 +
 +
beta=0.54 +- 0.22, alpha=2.68 +-1.13
 +
 +
 +
//K1*L(1/m)  er K1*L    sgima^2(mm)  er sigma^2
 +
 +
[[Media:2010_Jul_Emit_refit_data_y.txt]]
 +
 +
 +
parabola fit for y-projection (y in mm unit):
 +
 +
y = (8.51813 +-0.40098) + (-3.88142+-0.28132)*x + (0.57350+-0.04792)*x.*x
 +
 +
Data created from parabola fit
 +
 +
[[Media:2010_Jul_Emit_data_from_par_fit_y.txt]]
  
  
  
 
Go back [[Positrons]]
 
Go back [[Positrons]]

Latest revision as of 07:01, 22 October 2012

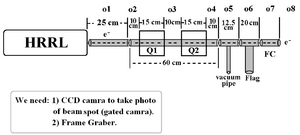
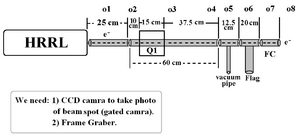
Design

Emittance Desien.png

New deisign: We changed to use just one magnet.


Emittance Desien new.png

File:Emittance Test Optim File.txt

HRRL had steer magnets on itself. We don't need external steer magnets. But Dr. Chouffani said that we might need them after quads, if the quads are not on axis. He will think about it.

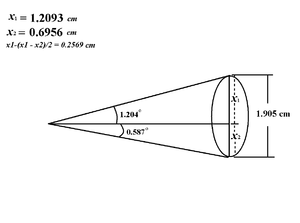
Beam Line design on 27th, Jul. 2010:

Emittance Desien 27th Jul 2010.png

HRRL Emittance Desien 27th Jul 2010.png

Optim File on 27th, Jul. 2010:

File:Emittance Test Optim File 27th Jul 2010.txt



File:HRRL Emittance.pdf

YAG (Yttrium Aluminum Garnet) Christal

YAG Christal for HRRL 2010 July Emittance Test.jpg


Faraday Cup

Farady Cap For HRRL Positorns 1.jpg Farady Cap For HRRL Positorns 2.jpg Farady Cap For HRRL Positorns 3.jpg Farady Cap For HRRL Positorns 4.jpg Farady Cap For HRRL Positorns 5.jpg Farady Cap For HRRL Positorns 6.jpg Farady Cap For HRRL Positorns 7.jpg Farady Cap For HRRL Positorns 8.jpg

Old Beam Line

HRRL Old BeamLine 1.jpg HRRL Old BeamLine 2.jpg HRRL Old BeamLine 3.jpg HRRL Old BeamLine 4.jpg HRRL Old BeamLine 5.jpg HRRL Old BeamLine 6.jpg

Beam Line Parts

Beam Line Parts HRRL Positorns 1.jpg Beam Line Parts HRRL Positorns 2.jpg Beam Line Parts HRRL Positorns 3.jpg Beam Line Parts HRRL Positorns 6.jpg Beam Line Parts HRRL Positorns 7.jpg Beam Line Parts HRRL Positorns 8.jpg Beam Line Parts HRRL Positorns 9.jpg Beam Line Parts HRRL Positorns 10.jpg Beam Line Parts HRRL Positorns 11.jpg Beam Line Parts HRRL Positorns 12.jpg


Length of the pole face of Quad2Tin z direction is 8 cm.

Beam Line Parts HRRL Positorns 4.jpg Beam Line Parts HRRL Positorns 5.jpg

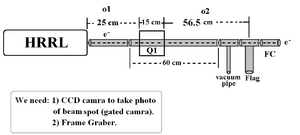
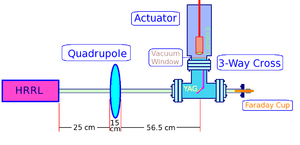
Constructed Beam Line for Emittance Test

Vacuum pressure on the beam line is less than [math] 10^{-8} [/math] torr (on 2010-July-7th).

Constructed Beam Line for Emittance Test 1.jpg Constructed Beam Line for Emittance Test 2.jpg Constructed Beam Line for Emittance Test 3.jpg

Leveling Survey

Downstream of the beam up by 2.6 mm.

Constructed Beam Line for Emittance Test Leveling Survey.jpg



How to do Leveling Survey and Alignment with Theodolite on e- Beam Line

A. Leveling Beam Pipe

1. Put the theodolite as high as the center of the beam line at upstream. Turn theodolite up and down. If the up angle is equal to down angle from the center of the pipe, theodolite is exactly as high as beam pipe. If not, adjust theodolite, until up and down angles are equal.

2. Once first step finished, then rotate theodolite horizontally to down stream. Turn it up and down, if up and down angles are not equal, adjust the stand till they are equal.


B. How to Make Sure the Quad is Perpendicular to the Beam Line

If the distances between quads and end of cavity at any given points are equal, then quad and end of cavity are parallel. Pipe is perpendicular to the end of the cavity, thus, magnet would also be perpendicular to the pipe.

I will find at lest three random points quads and three corresponding points at the end of the cavity, make sure they are equal, then I can say, magnet is perpendicular to the beam line.

I am planning to stick a metal ruler two, so two faces are parallel.


C. Centering the Quad Magnet with Theodolite

Vertical Centering

1. Finish the step 1 in A.

2. Then turn up the theodolite from the upper edge of the pipe to the magnet hole, call this angle upper angle. Do the same at lower part, call it lower angle. If the this two angles are not equal adjust the stand till they are equal.


Horizantal Centering

We know the diameter of the pipe [math] d_p [/math]. So, we can calculate from the pipe to the edge of the quad as:

Calculate from the Pipe to the edge of the Quad.jpg

We need to make sure this distance is same when measure it horizontally, so that our quad is centered on the pipe. I am going to use a ruler to ...(thinking)


July 2010 Run

Initial Accelerator Settings

E = 10 MeV [math]\Rightarrow[/math] Control Voltage= 4.09 V

Pulse Width <= 50 ns

Average Beam Current = least amount needed to light up YaG crystal, start at 1 mA and Rep rate of 100 Hz.

At the same time we want to do radiation test on HRRL. This is for predicting the radiation after shifting cavity to new position. Radiation test run plan is at: [1]

7/26/10

Alignment check

1.) Survey the Quad to be sure it is centered on the beam pipe

2.) survey the flag to determine if target is centered on the beam pipe

Transmission tuning

1.) Using the quads and accelerator coils, focus the beam on the YaG crystal to as fine a spot as possible. Monitor the FC during the focusing.

changed control Voltage from

Control Voltage= 4.9 V [math]\Rightarrow[/math] E = 16 MeV

to


4.09 V [math]\Rightarrow[/math] E = 10 MeV


Tune the 4 accelerator coils for max transmission.

We want to maximize the current reach the Farady Cup. This can be determined by the ratio on Channels of FC and Gun Current.

Gun current is the current on the pick up coil, which is input current for cavity. Current on Farady cup is the current reach the end of the beam line (FC is at the end of the beam line). We want to maximize the the ratio of Farady cup current to Gun current (FCC/GC), so there are more electrons will make it to the target. Thus, we enlarge our positron yield.

Basic principle: Fix three coils, change one till it maximized.


Coil 1 upstream left/right (mA) Coil 2 upstream UP/down (mA) Coil 3 downstream up/down Coil 4 downstream left right Scope Picture Gun Current FC current Transmission [math]\equiv[/math] Gun / FC
10 Run1 2-26-10.png 15 +/- 0.65 nV s -5.4[math]\pm[/math]1.8 nV s 36 [math]\pm[/math] 12 %


The HRRL went down after 2 hours of operation.

7/27/10

No HRRL beam time today. Chad tested the Thermatron module and believes it is not the problem. Chad will continue debugging tomorrow.


Filament

HRRL Emitt Test Filament On Without Light.jpg HRRL Emitt Test Filament On Yag 1.jpg HRRL Emitt Test Filament On Yag 2.jpg HRRL Emitt Test Filament On Yag 3.jpg HRRL Emitt Test Filament On Yag 4.jpg HRRL Emitt Test Filament On Yag 5.jpg HRRL Emitt Test Filament On Yag 6.jpg

BMP format:

Wiki won't allow me to upload with bmp extension. So, I used png extension to upload. After download files, you will find they are still with bmp extension.

HRRL Emitt Test Filament On Yag Without Light.png HRRL Emitt Test Filament On Yag With Light 1.png HRRL Emitt Test Filament On Yag With Light 2.png HRRL Emitt Test Filament On Yag With Light 3.png HRRL Emitt Test Filament On Yag With Light 4.png HRRL Emitt Test Filament On Yag With Light 5.png

7/28/10

The HRRL came back around 3pm today. A capacitor in the bank was found to be the problem.


Maximize Transmission

Maximized setup according to the accelerator operator.

Beam Energy: 16 MeV

Rep Rate: 95 Hz

Pulse Width: 100 ns

Coil 1 upstream left/right (A) Coil 2 upstream UP/down (A) Coil 3 downstream up/down (A) Coil 4 downstream left right (A) Scope Picture Gun Current FC current Ratio Spot Size
0.1 0.5 3.1 0.7 HRRL Emit Test Run1 7-28-10Spot Size.jpg


Reversed the polarities on coil # 3 and coil # 4. Rep rate: 3Hz

Coil 1 upstream left/right (A) Coil 2 upstream UP/down (A) Coil 3 downstream up/down (A) Coil 4 downstream left right (A) Scope Picture Gun Current FC current Ratio Spot Size
1.2 1.2 0.0 3 HRRL Emit Test Run1 7-28-10Spot Size2.jpg


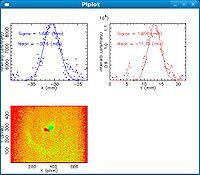
After image manipulation in GIMP to remove spot from the filament, Arne obtained reasonable projections for horizontal and vertical beam sizes ( < 2 mm). The quad was off, low rep rate to avoid saturation, 10MeV. This was the spot for the initial setup on Wednesday. Image fit snapshot 20100728 1720.jpg


Electron beam deflection due to Earth's B-field.

It appears the the image from electrons hitting the YaG crystal is offset (to the right) compare to the image from the filament which appears near the center of the cross hairs.

Is the earths Magnetic field causing the electrons to move this far beam right?

[math]B_{Earth}[/math] = 0.00005 Tesla ( [math]\frac{ \mbox{kg}}{\mbox{C}\cdot \mbox{s}}[/math]) = 0.5 Gauss

E_{electron} = 10 MeV = Pc [math]\Rightarrow[/math] P = 10 MeV/c

Estimation using Classical Lorentz Force (forget about angle of B and V)

[math]\vec{F} = q \vec{v} \times \vec{B}[/math]

assuming [math]v[/math] and [math]B[/math] are orthogonal then we get the cyclotron radius


[math]F= qvB = m\frac{v^2}{r} \Rightarrow r = \frac{qB}{mv}[/math]

[math]r = \frac{(1.6 \times 10^{-19} \mbox{C}) \times ( 5 \times 10^{-5}\frac{\mbox{kg}}{\mbox{C} \cdot \mbox{s}})}{mv}[/math]

[math]mv = P = 10 \frac{ \mbox{MeV}}{\mbox{c}} = 5.6 \times 10^{-21} \frac{\mbox{kg} \cdot \mbox{m} }{\mbox{s}} [/math]


[math]\Rightarrow r = 700 \mbox{m}[/math]


Now some Geometry.

Assuming the orbit is a circle with a 700 m radius, then the question becomes how far does the electron move to maintain the orbit if it travels 1 m in a straight line.

let

[math]r[/math]= radius of circle

[math]l[/math]= distance along the beam line

[math]d[/math] = deflection due to gravity

Note
[math]l[/math] is a tangent to the orbit

one can construct a right angle triangle with side of length d, the [math]l[/math] as the base and [math]r+d[/math] as the hypotenuse.

Then Pythagorean's theorem gives

[math]r^2 + l^2 = (r+d)^2[/math]

Giving

[math]d^2+ (2r)d +l^2 =0[/math]

using quadratic formula you get

[math]2d = -(2r)/2 \pm \sqrt{(2r)^2 + 4\frac{l^2}{r^2}}/2[/math]


since l/r is very small (1/700) we can approximate this as

[math]d = -r \pm r \sqrt{1+ \frac{l^2}{r^2}} \approx \frac{l^2}{r} = \frac{l^2}\frac{P}{qB}= \frac{qBl^2}{P}[/math]

for 10 MeV and a 1 m long beam pipe

[math]d = (l\mbox {m})^2 \frac{(1.6 \times 10^{-19} \mbox{C}) \times ( 5 \times 10^{-5}\frac{\mbox{kg}}{\mbox{C} \cdot \mbox{s}})}{ 5.6 \times 10^{-21} \frac{\mbox{kg} \cdot \mbox{m} }{\mbox{s}} } = l^2 \times 1.42 \mbox{mm}[/math] where [math]l[/math] is in units of m

Radiation Footprint Measurements

Spent the remaining beam time doing radiation footprint measurements.

HRRL_radiation_tests#Run_Plan

7/29/10

Today we first tune up the beam for max transmission.

If the above calculation is correct we can expect the electron beam to move at least 2 mm away from the center of the FC. We could test it the Earth's B-field is the cause of the deflection by watch the deflection as a function of the beam energy. If we had enough [math]\mu[/math]-metal we could wrap the beam pipe in it and see if the deflection goes away.

Quad Scan

First Scan

Beam current
[math]\frac{535.4 \pm 23.4 \times 10^{-12} \;\mbox{V} \cdot \mbox{s} }{50 \Omega} = 10.71 \pm 0.478 \times 10^{-12}\mbox{ C}[/math]
[math]\frac{10.71 \pm 0.478 \times 10^{-12}\mbox{ C}}{105 \times 10^{-9}\; \mbox{s}} = 102 \pm 4.46 \mu \mbox{A peak current}[/math]

HRRL Emit test Quad Scan First beam current.png HRRL Emit test Quad Scan First current pulse width fwhm.png

HRRL Emit test Quad Scan First 0Amp.jpg HRRL Emit test Quad Scan First 1Amp.jpg HRRL Emit test Quad Scan First 1.4Amp.jpg HRRL Emit test Quad Scan First 2Amp.jpg HRRL Emit test Quad Scan First 3Amp.jpg HRRL Emit test Quad Scan First 4Amp.jpg HRRL Emit test Quad Scan First 5Amp.jpg HRRL Emit test Quad Scan First 6Amp.jpg HRRL Emit test Quad Scan First 7Amp.jpg HRRL Emit test Quad Scan First 8Amp.jpg HRRL Emit test Quad Scan First 9Amp.jpg HRRL Emit test Quad Scan First 10Amp.jpg HRRL Emit test Quad Scan First 11Amp.jpg HRRL Emit test Quad Scan First 12Amp.jpg HRRL Emit test Quad Scan First 13Amp.jpg HRRL Emit test Quad Scan First 14Amp.jpg HRRL Emit test Quad Scan First 15Amp.jpg HRRL Emit test Quad Scan First 16Amp.jpg HRRL Emit test Quad Scan First 17Amp.jpg HRRL Emit test Quad Scan First 18Amp.jpg HRRL Emit test Quad Scan First 19Amp.jpg HRRL Emit test Quad Scan First 20Amp.jpg

HRRL Emit test Quad Scan First No Rf Background.jpg

Second Scan (Polarity Changed)

HRRL Emit test Quad Scan First beam current.png HRRL Emit test Quad Scan First current pulse width fwhm.png

HRRL Emit test Quad Scan Second 0Amp.jpg HRRL Emit test Quad Scan Second 1Amp.jpg HRRL Emit test Quad Scan Second 2Amp.jpg HRRL Emit test Quad Scan Second 3Amp.jpg HRRL Emit test Quad Scan Second 4Amp.jpg HRRL Emit test Quad Scan Second 5Amp.jpg HRRL Emit test Quad Scan Second 6Amp.jpg HRRL Emit test Quad Scan Second 7Amp.jpg HRRL Emit test Quad Scan Second 8Amp.jpg HRRL Emit test Quad Scan Second 9Amp.jpg HRRL Emit test Quad Scan Second 10Amp.jpg HRRL Emit test Quad Scan Second 11Amp.jpg HRRL Emit test Quad Scan Second 12Amp.jpg HRRL Emit test Quad Scan Second 13Amp.jpg HRRL Emit test Quad Scan Second 14Amp.jpg HRRL Emit test Quad Scan Second 15Amp.jpg HRRL Emit test Quad Scan Second 16Amp.jpg HRRL Emit test Quad Scan Second 17Amp.jpg HRRL Emit test Quad Scan Second 18Amp.jpg HRRL Emit test Quad Scan Second 19Amp.jpg HRRL Emit test Quad Scan Second 20Amp.jpg

HRRL Emit test Quad Scan Second 22Amp.jpg HRRL Emit test Quad Scan Second 14Amp 2.jpg HRRL Emit test Quad Scan Second 10Amp 2.jpg HRRL Emit test Quad Scan Second 5Amp 2.jpg HRRL Emit test Quad Scan Second 0Amp 2.jpg

PS Output Current to Shunt Resistance Current Conversion

PS negative connected to Quad positive.

Shunt resistance: 50 AMP, 50 MV. (PR 0050, QECO)


PS Reading (Amps) Shunt Resistance Voltage (mV) Shunt Resistance Current (Amps) (Calculated)
0 0 0
1 1 1
2 2.1 2.1
3 3.2 3.2
4 4.3 4.3
5 5.4 5.4
6 6.4 6.4
7 7.4 7.4
8 8.5 8.5
9 9.6 9.6
10 10.7 10.7
11 11.7 11.7
12 12.8 12.8
13 13.9 13.9
14 14.9 14.9
15 16 16
16 17 17
17 18.1 18.1
18 19.2 19.2
19 20.3 20.3
20 21.3 21.3
21 22.4 22.4
22 23.5 23.5



HRRL Emit test Quad Scan Scond No Rf Background 1.jpg HRRL Emit test Quad Scan Scond No Rf Background 2.jpg HRRL Emit test Quad Scan Scond No Rf Background Light on.jpg

Radiation Footprint Measurements

spent noon to 3pm on radiation measurements below

HRRL_radiation_tests#29_Jul_2010

Earth's B-field effect

It the above calculation on the effects of the Earth's Magnetic field on a the electron beam is correct then we should see the amount of deflection depend inversely on the electron's momentum (1/P).

So lets take a few pictures at the energy exterma to see how far the electron spot moves away from the filament image on the crystal.


E beam (V gun) YaG picture Beam Spot posiiton (arb offset)
5 100 px
10 (4.09 V) BeamSpot E10 7-29-10.jpg -31.8 [math]\pm[/math] .1 mm
16 (4.9 V) BeamSpot E16 7-29-10.jpg -32.0 [math]\pm[/math] 0.1 mm


We did not see the beam spot move when the energy was changed from 10 MeV to 16 MeV, but going to lower energy definitely moved the beam spot farther away from the center filament image that is located on the YaG crystal cross hairs.

Maximize Transmission

Change the linac coils to determine a setting which delivers the maximum current to the FC and has a reasonable spot size on the YaG viewer.


Coil 1 upstream left/right (A) Coil 2 upstream UP/down (A) Coil 3 downstream up/down Coil 4 downstream left right Scope Picture Gun Current FC current Ratio YaG Image
0 0.6 1.8 2.7


Coil 1 upstream left/right (A) Coil 2 upstream UP/down (A) Coil 3 downstream up/down Coil 4 downstream left right Scope Picture Gun Current FC current Ratio YaG Image
0 0.6 1.8 2.7 100px 100px



a.) Does a small beam spot size on the crystal give maximum FC signal?

b.) Is there a point where the spot size changes and you can't resolve a change in the FC output?

c.) Remove the YaG target and determine if above observations are unchanged.

Pickup Coil Calibration

2.) After tuning the beam to deliver the Maximum beam current to the FC, measure the FC and green pickup coil output as a function of current by integrating the pulse with an oscilloscope.

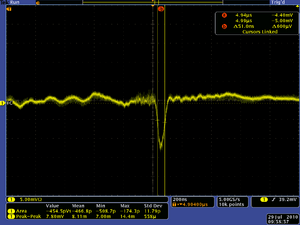
FC output Green Pickup Coil output Spot on Crystal Scope
(mA) (mA)
0.5 HRRL Emit test PickUp Coil Calibration 0.5mA Scope.jpg HRRL Emit test PickUp Coil Calibration 0.5mA Spot.png
1 HRRL Emit test PickUp Coil Calibration 1mA Scope.jpg HRRL Emit test PickUp Coil Calibration 1mA Spot.png
1.5 HRRL Emit test PickUp Coil Calibration 1.5mA Scope.jpg HRRL Emit test PickUp Coil Calibration 1.5mA Spot.png
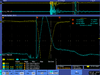
2 HRRL Emit test PickUp Coil Calibration 2mA Scope.jpg HRRL Emit test PickUp Coil Calibration 2mA Spot.png
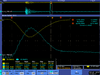
2.5 HRRL Emit test PickUp Coil Calibration 2.5mA Scope.jpg HRRL Emit test PickUp Coil Calibration 2.5mA Spot.png
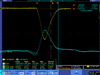
3 HRRL Emit test PickUp Coil Calibration 3mA Scope.jpg HRRL Emit test PickUp Coil Calibration 3mA Spot.png
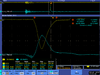
3.5 HRRL Emit test PickUp Coil Calibration 3.5mA Scope.jpg HRRL Emit test PickUp Coil Calibration 3.5mA Spot.png
4 HRRL Emit test PickUp Coil Calibration 4mA Scope.jpg HRRL Emit test PickUp Coil Calibration 4mA Spot.png
4.5 HRRL Emit test PickUp Coil Calibration 4.5mA Scope.jpg HRRL Emit test PickUp Coil Calibration 4.5mA Spot.png
5 HRRL Emit test PickUp Coil Calibration 5mA Scope.jpg HRRL Emit test PickUp Coil Calibration 5mA Spot.png
5.5 HRRL Emit test PickUp Coil Calibration 5.5mA Scope.jpg HRRL Emit test PickUp Coil Calibration 5.5mA Spot.png
6 HRRL Emit test PickUp Coil Calibration 6mA Scope.jpg HRRL Emit test PickUp Coil Calibration 6mA Spot.png

a.) does the FC output change with rep rate? It should not but maybe there is loss at high rates?

Quad scan

Tune the beam so a change in the quad B-field does not cause a deflection.

First attempt to measure the spot size change as a function of Quad current

Quad Current Beam Spot RMS (0 degrees= Left/right) Beam Spot RMS (90 degrees= Up/Down)
(Amps) (mm) (mm)


Shall we do both polarities?

Imaging

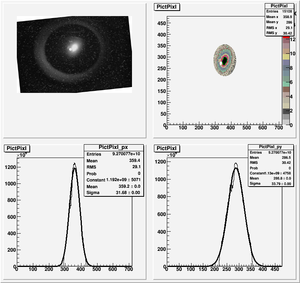
Background subtraction

The filament produces at least a 2 mm diameter spot on the YaG crystal. Beam dominates the image.

7/30/10

At 4pm yesterday we attempted to measure the emittance at high currents of 10 mA, previous measurements were at 0.3 mA. The beam spot became larger than the 1" YaG target holder. This would make emittance measurements impossible.

In order to measure the emittance above 1 mA we will need to insert a doublet as close to the accelerator entrance as possible. Since this would not be done by today we decided to cancel today's beam time and work on the next emittance measurement.

The YaG camera saturated at about 0.6 mA of beam current (our measurements were made at about 0.3 mA). Perhaps we should use a thin Aluminum target instead of the YaG crystal for high current measurements.

We were able to Trigger the GigE camera. We should use this next time.

Imaging scratch area

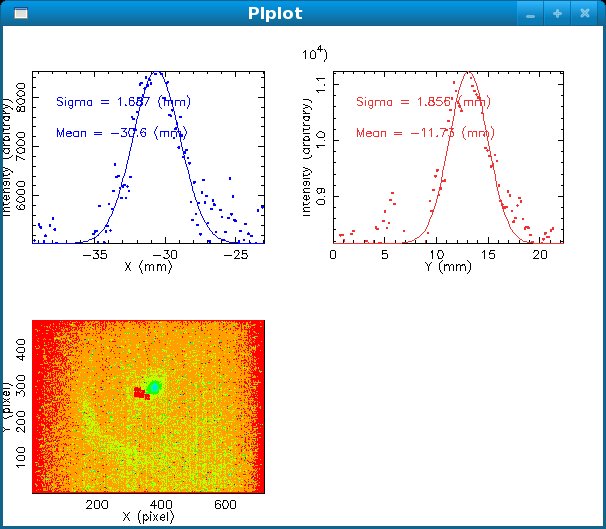
After image manipulation in GIMP to remove spot from filament. Obtained reasonable projections for horizontal and vertical beam sizes. The quad was off, low rep rate to avoid saturation, 10MeV. This was the spot for the initial setup on Wednesday. Image fit snapshot 20100728 1720.jpg



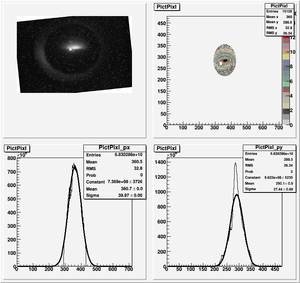
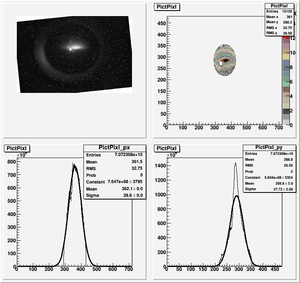
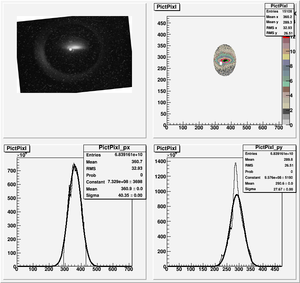
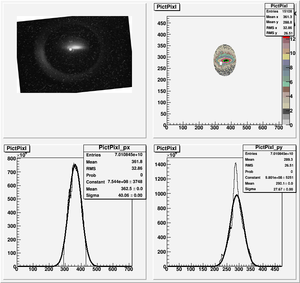
Data Analysis

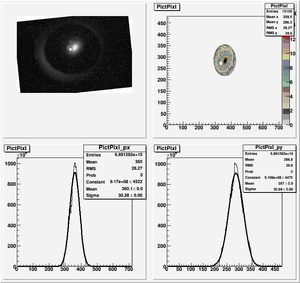
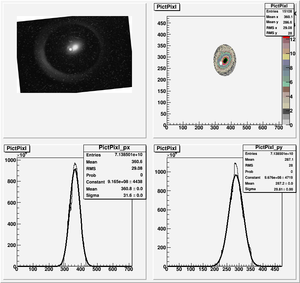
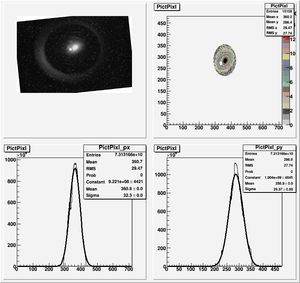
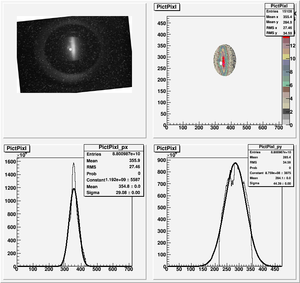
Root Code: File:Pixle.C

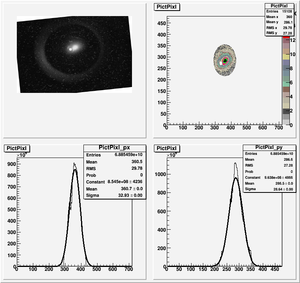
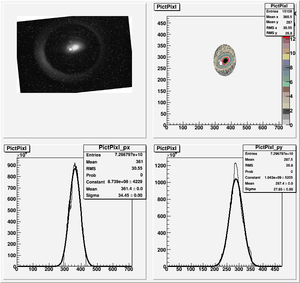
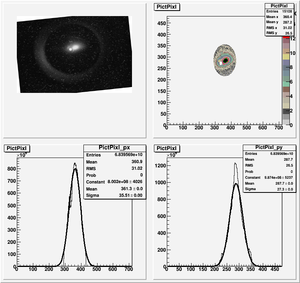
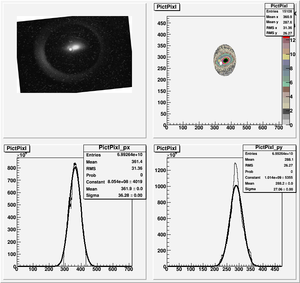
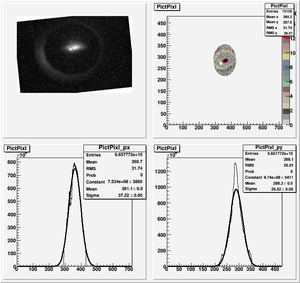
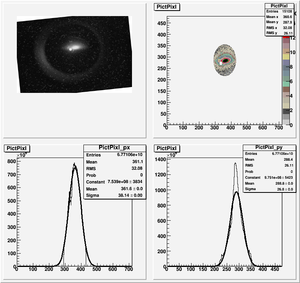
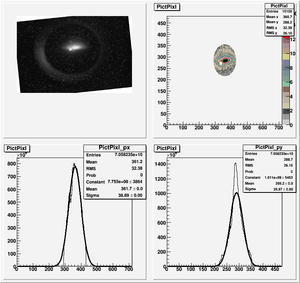
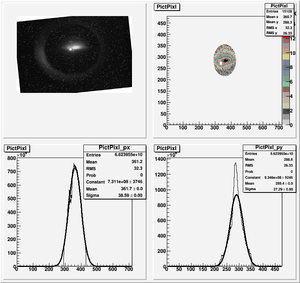
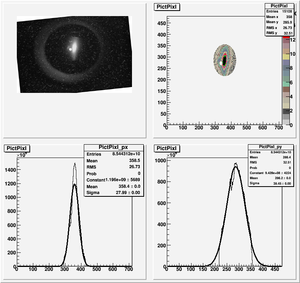
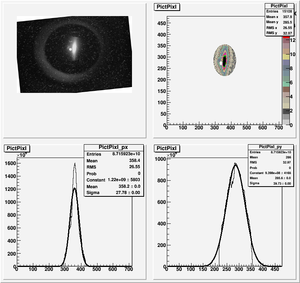
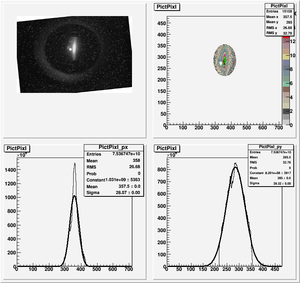
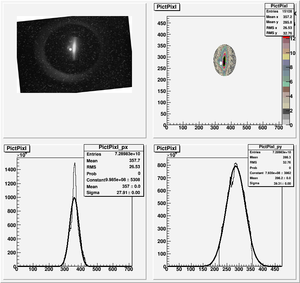
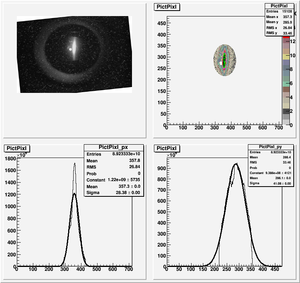
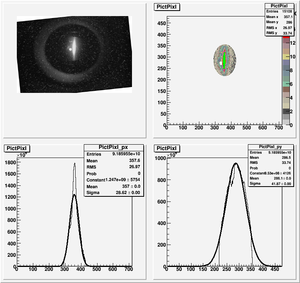
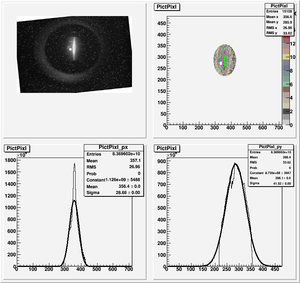
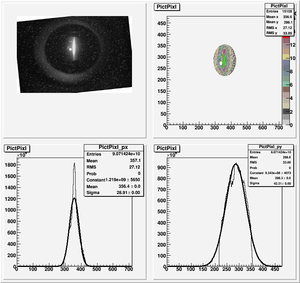
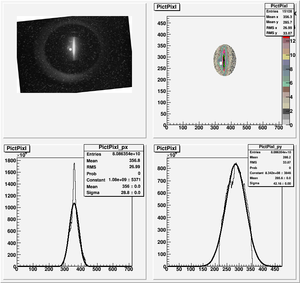
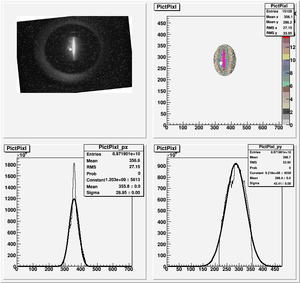
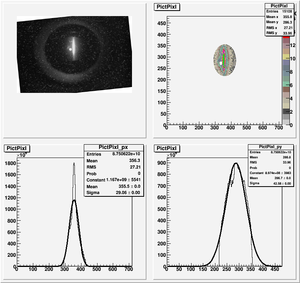
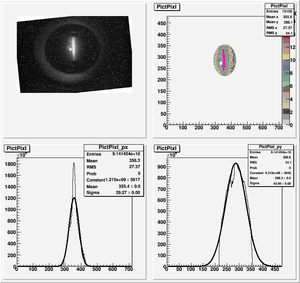
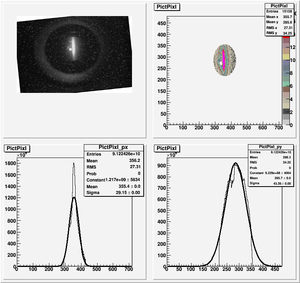
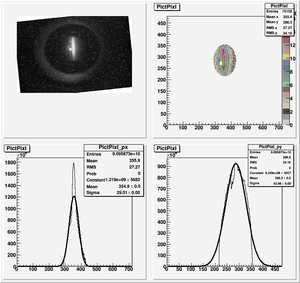
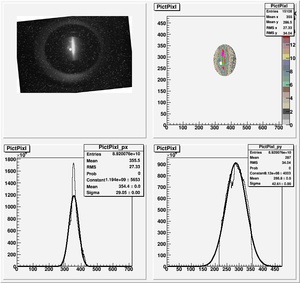
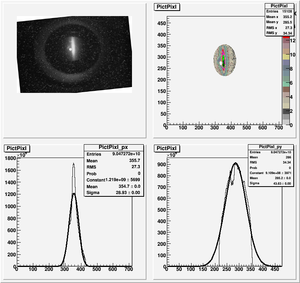
The cut is changed from circular to elliptical on Sep. 23rd, 2010.

Rotating the Image

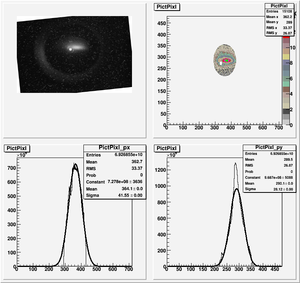
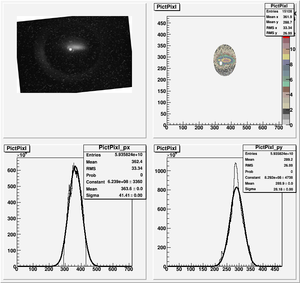
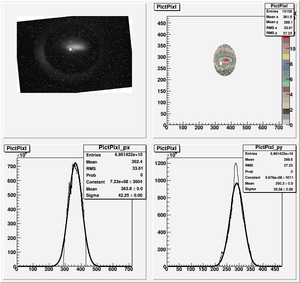
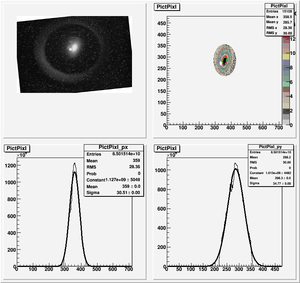
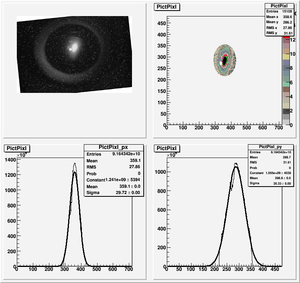
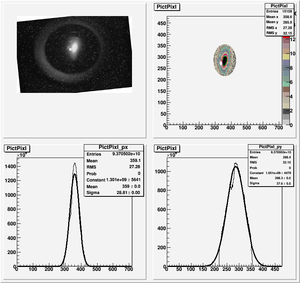
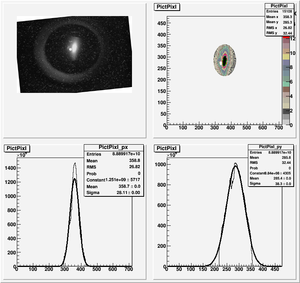
Images need to be rotated -6 degree, so cross at center of the crystal is perpendicular to the image. Here are the rotated images


1st Scan

Rotated HRRL Emit test Quad Scan First 0Amp.jpg Rotated HRRL Emit test Quad Scan First 1Amp.jpg Rotated HRRL Emit test Quad Scan First 1.4Amp.jpg Rotated HRRL Emit test Quad Scan First 2Amp.jpg Rotated HRRL Emit test Quad Scan First 3Amp.jpg Rotated HRRL Emit test Quad Scan First 4Amp.jpg Rotated HRRL Emit test Quad Scan First 5Amp.jpg Rotated HRRL Emit test Quad Scan First 6Amp.jpg Rotated HRRL Emit test Quad Scan First 7Amp.jpg Rotated HRRL Emit test Quad Scan First 8Amp.jpg Rotated HRRL Emit test Quad Scan First 9Amp.jpg Rotated HRRL Emit test Quad Scan First 10Amp.jpg Rotated HRRL Emit test Quad Scan First 11Amp.jpg Rotated HRRL Emit test Quad Scan First 12Amp.jpg Rotated HRRL Emit test Quad Scan First 13Amp.jpg Rotated HRRL Emit test Quad Scan First 14Amp.jpg Rotated HRRL Emit test Quad Scan First 15Amp.jpg Rotated HRRL Emit test Quad Scan First 16Amp.jpg Rotated HRRL Emit test Quad Scan First 17Amp.jpg Rotated HRRL Emit test Quad Scan First 18Amp.jpg Rotated HRRL Emit test Quad Scan First 19Amp.jpg Rotated HRRL Emit test Quad Scan First 20Amp.jpg

Rotated HRRL Emit test Quad Scan First No Rf Background.jpg


2nd Scan

Rotated HRRL Emit test Quad Scan Second 0Amp.jpg Rotated HRRL Emit test Quad Scan Second 1Amp.jpg Rotated HRRL Emit test Quad Scan Second 2Amp.jpg Rotated HRRL Emit test Quad Scan Second 3Amp.jpg Rotated HRRL Emit test Quad Scan Second 4Amp.jpg Rotated HRRL Emit test Quad Scan Second 5Amp.jpg Rotated HRRL Emit test Quad Scan Second 6Amp.jpg Rotated HRRL Emit test Quad Scan Second 7Amp.jpg Rotated HRRL Emit test Quad Scan Second 8Amp.jpg Rotated HRRL Emit test Quad Scan Second 9Amp.jpg Rotated HRRL Emit test Quad Scan Second 10Amp.jpg Rotated HRRL Emit test Quad Scan Second 11Amp.jpg Rotated HRRL Emit test Quad Scan Second 12Amp.jpg Rotated HRRL Emit test Quad Scan Second 13Amp.jpg Rotated HRRL Emit test Quad Scan Second 14Amp.jpg Rotated HRRL Emit test Quad Scan Second 15Amp.jpg Rotated HRRL Emit test Quad Scan Second 16Amp.jpg Rotated HRRL Emit test Quad Scan Second 17Amp.jpg Rotated HRRL Emit test Quad Scan Second 18Amp.jpg Rotated HRRL Emit test Quad Scan Second 19Amp.jpg Rotated HRRL Emit test Quad Scan Second 20Amp.jpg

HRRL Emit test Quad Scan Second 22Amp.jpg

Polarity was switched from 1st scan.

Fits for Beam Spot Projection

1st Scan

Fit Rotated HRRL Emit test Quad Scan First 0Amp.jpg Fit Rotated HRRL Emit test Quad Scan First 1Amp.jpg Fit Rotated HRRL Emit test Quad Scan First 1.4Amp.jpg

Fit Rotated HRRL Emit test Quad Scan First 2Amp.jpg Fit Rotated HRRL Emit test Quad Scan First 3Amp.jpg Fit Rotated HRRL Emit test Quad Scan First 4Amp.jpg

Fit Rotated HRRL Emit test Quad Scan First 5Amp.jpg Fit Rotated HRRL Emit test Quad Scan First 6Amp.jpg Fit Rotated HRRL Emit test Quad Scan First 7Amp.jpg

Fit Rotated HRRL Emit test Quad Scan First 8Amp.jpg Fit Rotated HRRL Emit test Quad Scan First 9Amp.jpg Fit Rotated HRRL Emit test Quad Scan First 10Amp.jpg

Fit Rotated HRRL Emit test Quad Scan First 11Amp.jpg Fit Rotated HRRL Emit test Quad Scan First 12Amp.jpg Fit Rotated HRRL Emit test Quad Scan First 13Amp.jpg

Fit Rotated HRRL Emit test Quad Scan First 14Amp.jpg Fit Rotated HRRL Emit test Quad Scan First 15Amp.jpg Fit Rotated HRRL Emit test Quad Scan First 16Amp.jpg

Fit Rotated HRRL Emit test Quad Scan First 17Amp.jpg Fit Rotated HRRL Emit test Quad Scan First 18Amp.jpg Fit Rotated HRRL Emit test Quad Scan First 19Amp.jpg

Fit Rotated HRRL Emit test Quad Scan First 20Amp.jpg


2nd Scan

Fit Rotated HRRL Emit test Quad Scan Second 0Amp.jpg Fit Rotated HRRL Emit test Quad Scan Second 1Amp.jpg Fit Rotated HRRL Emit test Quad Scan Second 2Amp.jpg

Fit Rotated HRRL Emit test Quad Scan Second 3Amp.jpg Fit Rotated HRRL Emit test Quad Scan Second 4Amp.jpg Fit Rotated HRRL Emit test Quad Scan Second 5Amp.jpg

Fit Rotated HRRL Emit test Quad Scan Second 6Amp.jpg Fit Rotated HRRL Emit test Quad Scan Second 7Amp.jpg Fit Rotated HRRL Emit test Quad Scan Second 8Amp.jpg

Fit Rotated HRRL Emit test Quad Scan Second 9Amp.jpg Fit Rotated HRRL Emit test Quad Scan Second 10Amp.jpg Fit Rotated HRRL Emit test Quad Scan Second 11Amp.jpg

Fit Rotated HRRL Emit test Quad Scan Second 12Amp.jpg Fit Rotated HRRL Emit test Quad Scan Second 13Amp.jpg Fit Rotated HRRL Emit test Quad Scan Second 14Amp.jpg

Fit Rotated HRRL Emit test Quad Scan Second 15Amp.jpg Fit Rotated HRRL Emit test Quad Scan Second 16Amp.jpg Fit Rotated HRRL Emit test Quad Scan Second 17Amp.jpg

Fit Rotated HRRL Emit test Quad Scan Second 18Amp.jpg Fit Rotated HRRL Emit test Quad Scan Second 19Amp.jpg Fit Rotated HRRL Emit test Quad Scan Second 20Amp.jpg

Fit Rotated HRRL Emit test Quad Scan Second 22Amp.jpg


Coil Current vs Beam Spot Projection Gaussian Fit's Sigma

1st Scan

Coil Current Reading on PS (Amps) Coil Current Reading From Shunt Resistance (Amps) X Projection Sigma (pixels) Y Projection Sigma (pixels)
0 0 30.28 30.69
1 1 31.6 29.81
1.4 32.3 29.37
2 2.1 32.93 2864
3 3.2 34.45 27.85
4 4.3 35.51 27.3
5 5.4 36.28 27.06
6 6.4 37.22 26.52
7 7.4 38.14 26.8
8 8.5 38.89 26.97
9 9.6 38.59 28.29
10 10.7 39.97 27.44
11 11.7 39.8 27.72
12 12.8 40.35 27.67
13 13.9 40.06 27.67
14 14.9 40.2 27.76
15 16 40.26 27.96
16 17 40.84 27.81
17 18.1 41.41 27.93
18 19.2 41.55 28.12
19 20.3 41.41 28.18
20 21.3 42.25 28.58


2nd Scan

Coil Current Reading on PS (Amps) Coil Current Reading From Shunt Resistance (Amps) X Projection Sigma (pixels) Y Projection Sigma (pixels)
0 0 31.68 33.79
1 1 30.51 34.77
2 2.1 29.72 36.33
3 3.2 28.81 37.6
4 4.3 28.11 38.3
5 5.4 27.99 38.45
6 6.4 27.78 39.73
7 7.4 28.07 39.32
8 8.5 27.91 39.31
9 9.6 28.38 41.08
10 10.7 28.62 41.87
11 11.7 28.66 41.52
12 12.8 28.91 42.31
13 13.9 28.8 42.16
14 14.9 28.95 42.41
15 16 29.06 42.58
16 17 29.27 42.95
17 18.1 29.15 43.26
18 19.2 29.01 42.98
19 20.3 29.05 42.61
20 21.3 28.93 43.63
22 23.5 29.08 44.39



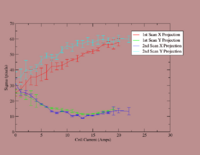
Multi-Fits for Beam Spot Projection

Multi-Fits 1st Scan

Naming the photos: Rotated_HRRL_Emit_Test_Quad_Scan_First_20Amp_Multi_Fit7 -> RHETQSF20AMF7


Coild Current (Amps) 1st Fit 2nd Fit 3rd Fit 4th Fit 5th Fit 6th Fit 7th Fit Mean and Error
0 RHETQSF0AMF1.png [math]{\sigma}_{x,y}= 21.4,22.5 [/math] RHETQSF0AMF2.png [math]{\sigma}_{x,y}= 25.5,23.2 [/math] RHETQSF0AMF3.png [math]{\sigma}_{x,y}= 22.9,24.5 [/math] RHETQSF0AMF4.png [math]{\sigma}_{x,y}= 28.2,25.0 [/math] RHETQSF0AMF5.png [math]{\sigma}_{x,y}= 26.1,25.7 [/math] RHETQSF0AMF6.png [math]{\sigma}_{x,y}= 26.6,28.2 [/math] RHETQSF0AMF7.png [math]{\sigma}_{x,y}= 26.3,27.3 [/math] [math]{\sigma}_{x,y}= 25.3\pm2.2 , 25.2 \pm1.9 [/math]
1 RHETQSF1AMF1.png [math]{\sigma}_{x,y}= 22.3,21.5 [/math] RHETQSF1AMF2.png [math]{\sigma}_{x,y}= 25.1,21.8 [/math] RHETQSF1AMF3.png [math]{\sigma}_{x,y}= 22.9,24.5 [/math] RHETQSF1AMF4.png [math]{\sigma}_{x,y}= 25.5,22.6 [/math] RHETQSF1AMF5.png [math]{\sigma}_{x,y}= 28.7,28.2 [/math] RHETQSF1AMF6.png [math]{\sigma}_{x,y}= 33.3,26.3 [/math] RHETQSF1AMF7.png [math]{\sigma}_{x,y}= 35.0,28.4 [/math] [math]{\sigma}_{x,y}= 27.5\pm4.6 , 24.8 \pm 2.7 [/math]
2 RHETQSF2AMF1.png [math]{\sigma}_{x,y}= 21.2,20.2 [/math] RHETQSF2AMF2.png [math]{\sigma}_{x,y}= 22.8,20.7 [/math] RHETQSF2AMF3.png [math]{\sigma}_{x,y}= 27.9,21.2 [/math] RHETQSF2AMF4.png [math]{\sigma}_{x,y}= 35.0,27.1 [/math] RHETQSF2AMF5.png [math]{\sigma}_{x,y}= 36.6,26.6 [/math] RHETQSF2AMF6.png [math]{\sigma}_{x,y}= 36.6,26.0 [/math] RHETQSF2AMF7.png [math]{\sigma}_{x,y}= 40.0,24.6 [/math] [math]{\sigma}_{x,y}= 31.4 \pm 6.9 , 23.8 \pm 2.8 [/math]
3 RHETQSF3AMF1.png [math]{\sigma}_{x,y}= 28.7,19.6 [/math] RHETQSF3AMF2.png [math]{\sigma}_{x,y}= 30.4,20.1 [/math] RHETQSF3AMF3.png [math]{\sigma}_{x,y}= 29.8,20.0 [/math] RHETQSF3AMF4.png [math]{\sigma}_{x,y}= 38.8,13.3 [/math] RHETQSF3AMF5.png [math]{\sigma}_{x,y}= 39.5,26.8 [/math] RHETQSF3AMF6.png [math]{\sigma}_{x,y}= 38.8,27.4 [/math] RHETQSF3AMF7.png [math]{\sigma}_{x,y}= 41.0,25.6 [/math] [math]{\sigma}_{x,y}= 35.3 \pm 5.0 , 21.8 \pm 4.7 [/math]
4 RHETQSF4AMF1.png [math]{\sigma}_{x,y}= 28.2,17.6 [/math] RHETQSF4AMF2.png [math]{\sigma}_{x,y}= 30.2,17.6 [/math] RHETQSF4AMF3.png [math]{\sigma}_{x,y}= 29.9,18.1 [/math] RHETQSF4AMF4.png [math]{\sigma}_{x,y}= 37.1,29.8 [/math] RHETQSF4AMF5.png [math]{\sigma}_{x,y}= 39.4,18.5 [/math] RHETQSF4AMF6.png [math]{\sigma}_{x,y}= 40.3,19.1 [/math] RHETQSF4AMF7.png [math]{\sigma}_{x,y}= 42.9,19.2 [/math] [math]{\sigma}_{x,y}= 35.4 \pm 5.5 , 20.0 \pm 4.1 [/math]
5 RHETQSF5AMF1.png [math]{\sigma}_{x,y}= 33.0,17.0 [/math] RHETQSF5AMF2.png [math]{\sigma}_{x,y}= 33.5,16.6 [/math] RHETQSF5AMF3.png [math]{\sigma}_{x,y}= 31.1,17.2 [/math] RHETQSF5AMF4.png [math]{\sigma}_{x,y}= 37.0,17.9 [/math] RHETQSF5AMF5.png [math]{\sigma}_{x,y}= 40.0,18.2 [/math] RHETQSF5AMF6.png [math]{\sigma}_{x,y}= 41.8,18.5 [/math] RHETQSF5AMF7.png [math]{\sigma}_{x,y}= 42.5,18.0 [/math] [math]{\sigma}_{x,y}= 37.0 \pm 4.2 , 17.6 \pm 0.6 [/math]
6 RHETQSF6AMF1.png [math]{\sigma}_{x,y}= 31.8,15.4 [/math] RHETQSF6AMF2.png [math]{\sigma}_{x,y}= 34.7,15.6 [/math] RHETQSF6AMF3.png [math]{\sigma}_{x,y}= 33.4,16.3 [/math] RHETQSF6AMF4.png [math]{\sigma}_{x,y}= 41.0,16.4 [/math] RHETQSF6AMF5.png [math]{\sigma}_{x,y}= 41.4,16.2 [/math] RHETQSF6AMF6.png [math]{\sigma}_{x,y}= 43.2,16.8 [/math] RHETQSF6AMF7.png [math]{\sigma}_{x,y}= 44.8,16.2 [/math] [math]{\sigma}_{x,y}= 38.6 \pm 4.8 , 16.1 \pm 0.4 [/math]
7 RHETQSF7AMF1.png [math]{\sigma}_{x,y}= 36.4,14.8 [/math] RHETQSF7AMF2.png [math]{\sigma}_{x,y}= 39.3,15.3 [/math] RHETQSF7AMF3.png [math]{\sigma}_{x,y}= 40.7,14.9 [/math] RHETQSF7AMF4.png [math]{\sigma}_{x,y}= 43.6,15.1 [/math] RHETQSF7AMF5.png [math]{\sigma}_{x,y}= 43.0,15.5 [/math] RHETQSF7AMF6.png [math]{\sigma}_{x,y}= 44.2,15.9 [/math] RHETQSF7AMF7.png [math]{\sigma}_{x,y}= 49.3,16.1 [/math] [math]{\sigma}_{x,y}= 42.4 \pm 3.8 , 15.4 \pm 0.5 [/math]
8 RHETQSF8AMF1.png [math]{\sigma}_{x,y}= 37.9,14.7 [/math] RHETQSF8AMF2.png [math]{\sigma}_{x,y}= 43.0,14.7 [/math] RHETQSF8AMF3.png [math]{\sigma}_{x,y}= 40.0,14.0 [/math] RHETQSF8AMF4.png [math]{\sigma}_{x,y}= 44.0,15.7 [/math] RHETQSF8AMF5.png [math]{\sigma}_{x,y}= 44.0,15.5 [/math] RHETQSF8AMF6.png [math]{\sigma}_{x,y}= 43.9,15.3 [/math] RHETQSF8AMF7.png [math]{\sigma}_{x,y}= 44.1,15.0 [/math] [math]{\sigma}_{x,y}= 42.4 \pm 2.3 , 15.0 \pm 0.5 [/math]
9 RHETQSF9AMF1.png [math]{\sigma}_{x,y}= 41.0,12.5 [/math] RHETQSF9AMF2.png [math]{\sigma}_{x,y}= 39.0,13.0 [/math] RHETQSF9AMF3.png [math]{\sigma}_{x,y}= 41.0,12.9 [/math] RHETQSF9AMF4.png [math]{\sigma}_{x,y}= 43.0,14.4 [/math] RHETQSF9AMF5.png [math]{\sigma}_{x,y}= 45.0,14.7 [/math] RHETQSF9AMF6.png [math]{\sigma}_{x,y}= 44.9,15.0 [/math] RHETQSF9AMF7.png [math]{\sigma}_{x,y}= 46.0,16.0 [/math] [math]{\sigma}_{x,y}= 42.8 \pm 2.4 , 14.1 \pm 1.2 [/math]
10 RHETQSF10AMF1.png [math]{\sigma}_{x,y}= 41.0,14.0 [/math] RHETQSF10AMF2.png [math]{\sigma}_{x,y}= 45.7,13.7 [/math] RHETQSF10AMF3.png [math]{\sigma}_{x,y}= 41.5,14.2 [/math] RHETQSF10AMF4.png [math]{\sigma}_{x,y}= 46.2,13.6 [/math] RHETQSF10AMF5.png [math]{\sigma}_{x,y}= 46.0,14.7 [/math] RHETQSF10AMF6.png [math]{\sigma}_{x,y}= 45.0,14.2 [/math] RHETQSF10AMF7.png [math]{\sigma}_{x,y}= 46.9,14.1 [/math] [math]{\sigma}_{x,y}= 44.6 \pm 2.2 , 14.4 \pm 0.3 [/math]
11 RHETQSF11AMF1.png [math]{\sigma}_{x,y}= 45.4,13.2 [/math] RHETQSF11AMF2.png [math]{\sigma}_{x,y}= 47.2,12.0 [/math] RHETQSF11AMF3.png [math]{\sigma}_{x,y}= 46.4,12.3 [/math] RHETQSF11AMF4.png [math]{\sigma}_{x,y}= 46.4,13.2 [/math] RHETQSF11AMF5.png [math]{\sigma}_{x,y}= 46.7,14.5 [/math] RHETQSF11AMF6.png [math]{\sigma}_{x,y}= 47.0,14.3 [/math] RHETQSF11AMF7.png [math]{\sigma}_{x,y}= 47.2,14.6 [/math] [math]{\sigma}_{x,y}= 46.6 \pm 0.6 , 13.5 \pm 1.0 [/math]
12 RHETQSF12AMF1.png [math]{\sigma}_{x,y}= 44.5,11.6 [/math] RHETQSF12AMF2.png [math]{\sigma}_{x,y}= 44.9,12.0 [/math] RHETQSF12AMF3.png [math]{\sigma}_{x,y}= 46.4,11.9 [/math] RHETQSF12AMF4.png [math]{\sigma}_{x,y}= 48.6,11.8 [/math] RHETQSF12AMF5.png [math]{\sigma}_{x,y}= 49.1,11.6 [/math] RHETQSF12AMF6.png [math]{\sigma}_{x,y}= 47.8,13.0 [/math] RHETQSF12AMF7.png [math]{\sigma}_{x,y}= 50.0,12.7 [/math] [math]{\sigma}_{x,y}= 47.3 \pm 2.0 , 12.1 \pm 0.5 [/math]
13 RHETQSF13AMF1.png [math]{\sigma}_{x,y}= 48.0,11.8 [/math] RHETQSF13AMF2.png [math]{\sigma}_{x,y}= 50.0,11.6 [/math] RHETQSF13AMF3.png [math]{\sigma}_{x,y}= 50.2,12.1 [/math] RHETQSF13AMF4.png [math]{\sigma}_{x,y}= 49.2,11.0 [/math] RHETQSF13AMF5.png [math]{\sigma}_{x,y}= 50.6,11.2 [/math] RHETQSF13AMF6.png [math]{\sigma}_{x,y}= 50.0,12.0 [/math] RHETQSF13AMF7.png [math]{\sigma}_{x,y}= 51.6,11.6 [/math] [math]{\sigma}_{x,y}= 49.9 \pm 1.0 , 11.6 \pm 0.4 [/math]
14 RHETQSF14AMF1.png [math]{\sigma}_{x,y}= 51.0,11.8 [/math] RHETQSF14AMF2.png [math]{\sigma}_{x,y}= 51.0,11.2 [/math] RHETQSF14AMF3.png [math]{\sigma}_{x,y}= 51.3,11.2 [/math] RHETQSF14AMF4.png [math]{\sigma}_{x,y}= 50.7,11.6 [/math] RHETQSF14AMF5.png [math]{\sigma}_{x,y}= 52.2,11.7 [/math] RHETQSF14AMF6.png [math]{\sigma}_{x,y}= 51.8,11.6 [/math] RHETQSF14AMF7.png [math]{\sigma}_{x,y}= 52.7,11.4 [/math] [math]{\sigma}_{x,y}= 51.5 \pm 0.7 , 11.5 \pm 0.2 [/math]
15 RHETQSF15AMF1.png [math]{\sigma}_{x,y}= 52.3,12.0 [/math] RHETQSF15AMF2.png [math]{\sigma}_{x,y}= 50.0,11.6 [/math] RHETQSF15AMF3.png [math]{\sigma}_{x,y}= 51.0,11.3 [/math] RHETQSF15AMF4.png [math]{\sigma}_{x,y}= 50.6,11.6 [/math] RHETQSF15AMF5.png [math]{\sigma}_{x,y}= 53.0,11.5 [/math] RHETQSF15AMF6.png [math]{\sigma}_{x,y}= 53.2,11.9 [/math] RHETQSF15AMF7.png [math]{\sigma}_{x,y}= 52.7,12.0 [/math] [math]{\sigma}_{x,y}= 51.8 \pm 1.2 , 11.7 \pm 0.3 [/math]
16 RHETQSF16AMF1.png [math]{\sigma}_{x,y}= 53.4,12.5 [/math] RHETQSF16AMF2.png [math]{\sigma}_{x,y}= 54.0,12.0 [/math] RHETQSF16AMF3.png [math]{\sigma}_{x,y}= 54.3,11.8 [/math] RHETQSF16AMF4.png [math]{\sigma}_{x,y}= 51.5,11.5 [/math] RHETQSF16AMF5.png [math]{\sigma}_{x,y}= 53.3,12.7 [/math] RHETQSF16AMF6.png [math]{\sigma}_{x,y}= 52.1,12.8 [/math] RHETQSF16AMF7.png [math]{\sigma}_{x,y}= 55.0,12.5 [/math] [math]{\sigma}_{x,y}= 53.4 \pm 1.1 , 12.3 \pm 0.5 [/math]
17 RHETQSF17AMF1.png [math]{\sigma}_{x,y}= 55.0,13.4 [/math] RHETQSF17AMF2.png [math]{\sigma}_{x,y}= 56.5,13.8 [/math] RHETQSF17AMF3.png [math]{\sigma}_{x,y}= 56.8,13.9 [/math] RHETQSF17AMF4.png [math]{\sigma}_{x,y}= 55.9,12.9 [/math] RHETQSF17AMF5.png [math]{\sigma}_{x,y}= 56.0,11.9 [/math] RHETQSF17AMF6.png [math]{\sigma}_{x,y}= 57.4,12.2 [/math] RHETQSF17AMF7.png [math]{\sigma}_{x,y}= 58.0,13.3 [/math] [math]{\sigma}_{x,y}= 56.5 \pm 0.9 , 13.1 \pm 0.7 [/math]
18 RHETQSF18AMF1.png [math]{\sigma}_{x,y}= 59.0,14.0 [/math] RHETQSF18AMF2.png [math]{\sigma}_{x,y}= 56.0,13.2 [/math] RHETQSF18AMF3.png [math]{\sigma}_{x,y}= 56.0,13.4 [/math] RHETQSF18AMF4.png [math]{\sigma}_{x,y}= 55.0,13.9 [/math] RHETQSF18AMF5.png [math]{\sigma}_{x,y}= 56.1,14.1 [/math] RHETQSF18AMF6.png [math]{\sigma}_{x,y}= 53.5,13.4 [/math] RHETQSF18AMF7.png [math]{\sigma}_{x,y}= 59.0,13.0 [/math] [math]{\sigma}_{x,y}= 56.4 \pm 1.9 , 13.6 \pm 0.4 [/math]
19 RHETQSF19AMF1.png [math]{\sigma}_{x,y}= 60.7,16.1 [/math] RHETQSF19AMF2.png [math]{\sigma}_{x,y}= 53.0,15.0 [/math] RHETQSF19AMF3.png [math]{\sigma}_{x,y}= 60.0,15.7 [/math] RHETQSF19AMF4.png [math]{\sigma}_{x,y}= 55.7,14.1 [/math] RHETQSF19AMF5.png [math]{\sigma}_{x,y}= 58.8,15.0 [/math] RHETQSF19AMF6.png [math]{\sigma}_{x,y}= 53.0,14.0 [/math] RHETQSF19AMF7.png [math]{\sigma}_{x,y}= 54.5,15.0 [/math] [math]{\sigma}_{x,y}= 56.5 \pm 3.0 , 15.0 \pm 0.7 [/math]
20 RHETQSF20AMF1.png [math]{\sigma}_{x,y}= 62.0,18.9 [/math] RHETQSF20AMF2.png [math]{\sigma}_{x,y}= 60.0,19.0 [/math] RHETQSF20AMF3.png [math]{\sigma}_{x,y}= 59.0,19.3 [/math] RHETQSF20AMF4.png [math]{\sigma}_{x,y}= 56.0,17.0 [/math] RHETQSF20AMF5.png [math]{\sigma}_{x,y}= 55.6,17.2 [/math] RHETQSF20AMF6.png [math]{\sigma}_{x,y}= 56.0,17.0 [/math] RHETQSF20AMF7.png [math]{\sigma}_{x,y}= 55.7,17.3 [/math] [math]{\sigma}_{x,y}= 57.8 \pm 2.4 , 18.0 \pm 1.0 [/math]

Multi-Fits 2nd Scan

Naming the photos: Rotated_HRRL_Emit_Test_Quad_Scan_Second_22Amp_Multi_Fit7 -> RHETQSS22AMF7

Coild Current (Amps) 1st Fit 2nd Fit 3rd Fit 4th Fit 5th Fit 6th Fit 7th Fit Mean and Error
0 RHETQSS0AMF1.png [math]{\sigma}_{x,y}=27.8,29.2 [/math] RHETQSS0AMF2.png [math]{\sigma}_{x,y}=28.4,30.5 [/math] RHETQSS0AMF3.png [math]{\sigma}_{x,y}=28.5,32.1 [/math] RHETQSS0AMF4.png [math]{\sigma}_{x,y}=29.8,37.4 [/math] RHETQSS0AMF5.png [math]{\sigma}_{x,y}=33.7,38.5 [/math] RHETQSS0AMF6.png [math]{\sigma}_{x,y}=33.4,38.6 [/math] RHETQSS0AMF7.png [math]{\sigma}_{x,y}=36.3,38.0 [/math] [math]{\sigma}_{x,y}=31.1 \pm 3.1,34.9\pm3.8 [/math]
1 RHETQSS1AMF1.png [math]{\sigma}_{x,y}=22.6,28.5 [/math] RHETQSS1AMF2.png [math]{\sigma}_{x,y}=24.5,30.7 [/math] RHETQSS1AMF3.png [math]{\sigma}_{x,y}=23.1,29.9 [/math] RHETQSS1AMF4.png [math]{\sigma}_{x,y}=27.4,41.0 [/math] RHETQSS1AMF5.png [math]{\sigma}_{x,y}=27.1,38.6 [/math] RHETQSS1AMF6.png [math]{\sigma}_{x,y}=26.5,39.8 [/math] RHETQSS1AMF7.png [math]{\sigma}_{x,y}=27.0,39.7 [/math] [math]{\sigma}_{x,y}= 25.5 \pm 1.9 , 35.5 \pm 5.1 [/math]
2 RHETQSS2AMF1.png [math]{\sigma}_{x,y}=23.5,32.9 [/math] RHETQSS2AMF2.png [math]{\sigma}_{x,y}=24.2,33.5 [/math] RHETQSS2AMF3.png [math]{\sigma}_{x,y}=22.7,34.7 [/math] RHETQSS2AMF4.png [math]{\sigma}_{x,y}=26.3,41.0 [/math] RHETQSS2AMF5.png [math]{\sigma}_{x,y}=26.8,45.8 [/math] RHETQSS2AMF6.png [math]{\sigma}_{x,y}=26.1,44.1 [/math] RHETQSS2AMF7.png [math]{\sigma}_{x,y}=26.5,48.9 [/math] [math]{\sigma}_{x,y}= 25.2 \pm 1.5 , 40.1 \pm 6.0 [/math]
3 RHETQSS3AMF1.png [math]{\sigma}_{x,y}=22.6,37.0 [/math] RHETQSS3AMF2.png [math]{\sigma}_{x,y}=22.9,36.4 [/math] RHETQSS3AMF3.png [math]{\sigma}_{x,y}=21.7,37.6 [/math] RHETQSS3AMF4.png [math]{\sigma}_{x,y}=23.8,39.5 [/math] RHETQSS3AMF5.png [math]{\sigma}_{x,y}=23.8,42.3 [/math] RHETQSS3AMF6.png [math]{\sigma}_{x,y}=24.1,42.3 [/math] RHETQSS3AMF7.png [math]{\sigma}_{x,y}=25.4,42.3 [/math] [math]{\sigma}_{x,y}=23.5 \pm 1.1 , 39.6\pm 2.5 [/math]
4 RHETQSS4AMF1.png [math]{\sigma}_{x,y}=19.9,38.8 [/math] RHETQSS4AMF2.png [math]{\sigma}_{x,y}=19.8,38.1 [/math] RHETQSS4AMF3.png [math]{\sigma}_{x,y}=19.1,39.3 [/math] RHETQSS4AMF4.png [math]{\sigma}_{x,y}=20.5,41.3 [/math] RHETQSS4AMF5.png [math]{\sigma}_{x,y}=20.8,42.2 [/math] RHETQSS4AMF6.png [math]{\sigma}_{x,y}=21.1,43.3 [/math] RHETQSS4AMF7.png [math]{\sigma}_{x,y}=21.4,44.4 [/math] [math]{\sigma}_{x,y}= 20.4\pm 0.8 , 41.1\pm 2.2 [/math]
5 RHETQSS5AMF1.png [math]{\sigma}_{x,y}=18.2,43.3 [/math] RHETQSS5AMF2.png [math]{\sigma}_{x,y}=18.0,45.9 [/math] RHETQSS5AMF3.png [math]{\sigma}_{x,y}=17.9,48.1 [/math] RHETQSS5AMF4.png [math]{\sigma}_{x,y}=18.2,47.9 [/math] RHETQSS5AMF5.png [math]{\sigma}_{x,y}=18.2,40.9 [/math] RHETQSS5AMF6.png [math]{\sigma}_{x,y}=17.0,48.5 [/math] RHETQSS5AMF7.png [math]{\sigma}_{x,y}=18.4,48.0 [/math] [math]{\sigma}_{x,y}= 18.0 \pm 0.4 , 46.1 \pm 2.7 [/math]
6 RHETQSS6AMF1.png [math]{\sigma}_{x,y}=16.4,47.0 [/math] RHETQSS6AMF2.png [math]{\sigma}_{x,y}=16.2,48.4 [/math] RHETQSS6AMF3.png [math]{\sigma}_{x,y}=15.7,50.6 [/math] RHETQSS6AMF4.png [math]{\sigma}_{x,y}=16.6,50.5 [/math] RHETQSS6AMF5.png [math]{\sigma}_{x,y}=16.5,46.9 [/math] RHETQSS6AMF6.png [math]{\sigma}_{x,y}=16.0,50.6 [/math] RHETQSS6AMF7.png [math]{\sigma}_{x,y}=16.3,50.6 [/math] [math]{\sigma}_{x,y}= 16.2 \pm 0.3 , 49.2\pm 1.6 [/math]
7 RHETQSS7AMF1.png [math]{\sigma}_{x,y}=13.1,44.5 [/math] RHETQSS7AMF2.png [math]{\sigma}_{x,y}=12.8,46.8 [/math] RHETQSS7AMF3.png [math]{\sigma}_{x,y}=13.2,49.3 [/math] RHETQSS7AMF4.png [math]{\sigma}_{x,y}=13.3,49.6 [/math] RHETQSS7AMF5.png [math]{\sigma}_{x,y}=13.7,45.2 [/math] RHETQSS7AMF6.png [math]{\sigma}_{x,y}=13.9,49.7 [/math] RHETQSS7AMF7.png [math]{\sigma}_{x,y}=12.8,49.6 [/math] [math]{\sigma}_{x,y}= 13.3\pm0.4 , 47.8\pm 2.1 [/math]
8 RHETQSS8AMF1.png [math]{\sigma}_{x,y}=12.3,49.0 [/math] RHETQSS8AMF2.png [math]{\sigma}_{x,y}=12.4,46.7 [/math] RHETQSS8AMF3.png [math]{\sigma}_{x,y}=11.7,49.3 [/math] RHETQSS8AMF4.png [math]{\sigma}_{x,y}=11.6,49.2 [/math] RHETQSS8AMF5.png [math]{\sigma}_{x,y}=13.1,45.0 [/math] RHETQSS8AMF6.png [math]{\sigma}_{x,y}=13.0,50.0 [/math] RHETQSS8AMF7.png [math]{\sigma}_{x,y}=12.3,49.6 [/math] [math]{\sigma}_{x,y}= 12.3\pm 0.5 , 48.4 \pm 1.7 [/math]
9 RHETQSS9AMF1.png [math]{\sigma}_{x,y}=13.3,50.4 [/math] RHETQSS9AMF2.png [math]{\sigma}_{x,y}=13.2,52.4 [/math] RHETQSS9AMF3.png [math]{\sigma}_{x,y}=13.1,55.7 [/math] RHETQSS9AMF4.png [math]{\sigma}_{x,y}=13.5,54.8 [/math] RHETQSS9AMF5.png [math]{\sigma}_{x,y}=13.3,50.0 [/math] RHETQSS9AMF6.png [math]{\sigma}_{x,y}=13.5,53.4 [/math] RHETQSS9AMF7.png [math]{\sigma}_{x,y}=13.2,54.5 [/math] [math]{\sigma}_{x,y}= 13.3 \pm 0.1 ,53.0 \pm 2.0 [/math]
10 RHETQSS10AMF1.png [math]{\sigma}_{x,y}=12.6,53.8 [/math] RHETQSS10AMF2.png [math]{\sigma}_{x,y}=13.0,54.9 [/math] RHETQSS10AMF3.png [math]{\sigma}_{x,y}=12.4,58.5 [/math] RHETQSS10AMF4.png [math]{\sigma}_{x,y}=12.9,57.7 [/math] RHETQSS10AMF5.png [math]{\sigma}_{x,y}=12.7,52.7 [/math] RHETQSS10AMF6.png [math]{\sigma}_{x,y}=12.8,55.0 [/math] RHETQSS10AMF7.png [math]{\sigma}_{x,y}=12.0,56.6 [/math] [math]{\sigma}_{x,y}= 12.6 \pm 0.3 , 55.6 \pm 1.9 [/math]
11 RHETQSS11AMF1.png [math]{\sigma}_{x,y}=10.1,52.2 [/math] RHETQSS11AMF2.png [math]{\sigma}_{x,y}=10.2,52.4 [/math] RHETQSS11AMF3.png [math]{\sigma}_{x,y}=9.8,58.3 [/math] RHETQSS11AMF4.png [math]{\sigma}_{x,y}=9.7,56.9 [/math] RHETQSS11AMF5.png [math]{\sigma}_{x,y}=10.9,51.3 [/math] RHETQSS11AMF6.png [math]{\sigma}_{x,y}=10.0,54.5 [/math] RHETQSS11AMF7.png [math]{\sigma}_{x,y}=9.7,55.4 [/math] [math]{\sigma}_{x,y}= 10.1 \pm 0.4 ,54.4 \pm 2.4 [/math]
12 RHETQSS12AMF1.png [math]{\sigma}_{x,y}=11.2,55.9 [/math] RHETQSS12AMF2.png [math]{\sigma}_{x,y}=10.8,55.0 [/math] RHETQSS12AMF3.png [math]{\sigma}_{x,y}=11.0,60.1 [/math] RHETQSS12AMF4.png [math]{\sigma}_{x,y}=10.5,59.8 [/math] RHETQSS12AMF5.png [math]{\sigma}_{x,y}=11.1,56.2 [/math] RHETQSS12AMF6.png [math]{\sigma}_{x,y}=10.4,56.4 [/math] RHETQSS12AMF7.png [math]{\sigma}_{x,y}=10.4,58.0 [/math] [math]{\sigma}_{x,y}= 10.8\pm 0.9, 57.3\pm1.8 [/math]
13 RHETQSS13AMF1.png [math]{\sigma}_{x,y}=8.9,54.8 [/math] RHETQSS13AMF2.png [math]{\sigma}_{x,y}=9.1,56.2 [/math] RHETQSS13AMF3.png [math]{\sigma}_{x,y}=8.7,60.4 [/math] RHETQSS13AMF4.png [math]{\sigma}_{x,y}=8.7,59.6 [/math] RHETQSS13AMF5.png [math]{\sigma}_{x,y}=9.1,53.5 [/math] RHETQSS13AMF6.png [math]{\sigma}_{x,y}=8.8,56.3 [/math] RHETQSS13AMF7.png [math]{\sigma}_{x,y}=8.7,57.1 [/math] [math]{\sigma}_{x,y}= 8.9 \pm 0.2 , 56.8 \pm 2.3 [/math]
14 RHETQSS14AMF1.png [math]{\sigma}_{x,y}=10.5,57.4 [/math] RHETQSS14AMF2.png [math]{\sigma}_{x,y}=10.9,56.0 [/math] File:RHETQSS14AMF3.png [math]{\sigma}_{x,y}=10.7,61.0 [/math] RHETQSS14AMF4.png [math]{\sigma}_{x,y}=10.7,60.7 [/math] RHETQSS14AMF5.png [math]{\sigma}_{x,y}=10.6,54.9 [/math] RHETQSS14AMF6.png [math]{\sigma}_{x,y}=10.9,60.6 [/math] RHETQSS14AMF7.png [math]{\sigma}_{x,y}=10.3,58.7 [/math] [math]{\sigma}_{x,y}= 10.7 \pm 0.2 , 58.5\pm 2.3 [/math]
15 RHETQSS15AMF1.png [math]{\sigma}_{x,y}=10.0,57.4 [/math] RHETQSS15AMF2.png [math]{\sigma}_{x,y}=10.8,55.2 [/math] RHETQSS15AMF3.png [math]{\sigma}_{x,y}=10.7,60.3 [/math] RHETQSS15AMF4.png [math]{\sigma}_{x,y}=10.5,58.7 [/math] RHETQSS15AMF5.png [math]{\sigma}_{x,y}=10.7,55.0 [/math] RHETQSS15AMF6.png [math]{\sigma}_{x,y}=10.3,57.4 [/math] RHETQSS15AMF7.png [math]{\sigma}_{x,y}=10.2,58.7 [/math] [math]{\sigma}_{x,y}= 10.5 \pm 0.3 , 57.5 \pm 1.8 [/math]
16 RHETQSS16AMF1.png [math]{\sigma}_{x,y}=10.5,60.6 [/math] RHETQSS16AMF2.png [math]{\sigma}_{x,y}=11.2,55.8 [/math] RHETQSS16AMF3.png [math]{\sigma}_{x,y}=11.5,63.4 [/math] RHETQSS16AMF4.png [math]{\sigma}_{x,y}=11.1,62.3 [/math] RHETQSS16AMF5.png [math]{\sigma}_{x,y}=12.0,56.8 [/math] RHETQSS16AMF6.png [math]{\sigma}_{x,y}=11.4,60.6 [/math] RHETQSS16AMF7.png [math]{\sigma}_{x,y}=11.3,56.0 [/math] [math]{\sigma}_{x,y}= 11.3 \pm 0.4 , 59.4 \pm 2.9 [/math]
17 RHETQSS17AMF1.png [math]{\sigma}_{x,y}= 12.2,57.6[/math] RHETQSS17AMF2.png [math]{\sigma}_{x,y}=13.6,58.7 [/math] RHETQSS17AMF3.png [math]{\sigma}_{x,y}=12.1,63.4 [/math] RHETQSS17AMF4.png [math]{\sigma}_{x,y}=11.2,57.4 [/math] RHETQSS17AMF5.png [math]{\sigma}_{x,y}=12.0,57.6 [/math] RHETQSS17AMF6.png [math]{\sigma}_{x,y}=12.0,58.7 [/math] RHETQSS17AMF7.png [math]{\sigma}_{x,y}=12.4,64.0 [/math] [math]{\sigma}_{x,y}= 12.2 \pm 0.7 , 59.6 \pm 2.6 [/math]
18 RHETQSS18AMF1.png [math]{\sigma}_{x,y}=11.4,59.7 [/math] RHETQSS18AMF2.png [math]{\sigma}_{x,y}=12.0,55.7 [/math] RHETQSS18AMF3.png [math]{\sigma}_{x,y}=13.2,61.4 [/math] RHETQSS18AMF4.png [math]{\sigma}_{x,y}=13.3,59.0 [/math] RHETQSS18AMF5.png [math]{\sigma}_{x,y}=12.5,58.5 [/math] RHETQSS18AMF6.png [math]{\sigma}_{x,y}=12.3,60.2 [/math] RHETQSS18AMF7.png [math]{\sigma}_{x,y}=11.9,58.3 [/math] [math]{\sigma}_{x,y}= 12.4 \pm 0.6 , 59.0\pm 1.7 [/math]
19 RHETQSS19AMF1.png [math]{\sigma}_{x,y}=19.99,59.0 [/math] RHETQSS19AMF2.png [math]{\sigma}_{x,y}=13.5,52.6 [/math] RHETQSS19AMF3.png [math]{\sigma}_{x,y}= 11.5,62.0[/math] RHETQSS19AMF4.png [math]{\sigma}_{x,y}=12.2 [/math] RHETQSS19AMF5.png [math]{\sigma}_{x,y}=11.86,59.6 [/math] RHETQSS19AMF6.png [math]{\sigma}_{x,y}=12.2,57.4 [/math] RHETQSS19AMF7.png [math]{\sigma}_{x,y}=13.0,55.0 [/math] [math]{\sigma}_{x,y}= 13.5 \pm 2.7 , 57.8 \pm 2.9 [/math]
20 RHETQSS20AMF1.png [math]{\sigma}_{x,y}= 13.29,60.73[/math] RHETQSS20AMF2.png [math]{\sigma}_{x,y}= 17.2,56.5[/math] RHETQSS20AMF3.png [math]{\sigma}_{x,y}= 13.3,59.8[/math] RHETQSS20AMF4.png [math]{\sigma}_{x,y}= 12.0,60.68[/math] RHETQSS20AMF5.png [math]{\sigma}_{x,y}= 12.84,63.72[/math] RHETQSS20AMF6.png [math]{\sigma}_{x,y}=14.0,59.3 [/math] RHETQSS20AMF7.png [math]{\sigma}_{x,y}= 13.7,61.2[/math] [math]{\sigma}_{x,y}= 13.8 \pm 1.5 , 60.3 \pm 2.0 [/math]
22 RHETQSS22AMF1.png [math]{\sigma}_{x,y}=19,61[/math] RHETQSS22AMF2.png [math]{\sigma}_{x,y}=12,55.7[/math] RHETQSS22AMF3.png [math]{\sigma}_{x,y}=13.2,61.7[/math] RHETQSS22AMF4.png [math]{\sigma}_{x,y}=13.3,59.0[/math] RHETQSS22AMF5.png [math]{\sigma}_{x,y}=11.3,62.4[/math] RHETQSS22AMF6.png [math]{\sigma}_{x,y}=12.3,60.2[/math] RHETQSS22AMF7.png [math]{\sigma}_{x,y}=11.9,58.3[/math] [math]{\sigma}_{x,y}= 13.3 \pm 2.4 , 59.8 \pm 2.1 [/math]


Current -vs- Sigma Data Files

First Scan:

File:HRRL Emitt Current vs Sigma 1stScan x.txt

File:HRRL Emitt Current vs Sigma 1stScan y.txt

HRRL Emitt Current vs Sigma 1stScan x.png HRRL Emitt Current vs Sigma 1stScan y.png

Second Scan:

File:HRRL Emitt Current vs Sigma 2ndScan x.txt

File:HRRL Emitt Current vs Sigma 2ndScan y.txt

HRRL Emitt Current vs Sigma 2ndScan x.png HRRL Emitt Current vs Sigma 2ndScan y.png

Current vs Sigma:

HRRL Emitt Current vs Sigma Fits.png


X projections:

File:HRRL Emitt Current vs Sigma Projections x.txt

HRRL Emitt Current vs Sigma Projections x.png

Fit:

P-value of this fit is less than 0.000001.

HRRL Emitt Current vs Sigma Fit Projections x.png



Y projections:

File:HRRL Emitt Current vs Sigma Projections y.txt

HRRL Emitt Current vs Sigma Projections y.png

Fit:

P-value of this fit is less than 0.000001.

HRRL Emitt Current vs Sigma Fit Projections y.png 



Next step: 
calibrate: mm/pxiel 
Parabola: All the x projections makeup one parabola, and y projections makeup one parabola. Put them in together.

Converting pixels to length

Diameter of circle inside crystal is 10 mm.

Convert the pictures to a histogram and measure pixels that way

Figures Horizontal Diameter (pixels) Vertical Diameter (pixels)
HRRL Emit Test July Run Converting pixels to length 1.png 91 59
HRRL Emit Test July Run Converting pixels to length 2.png 90 59
HRRL Emit Test July Run Converting pixels to length 3.png 90 59
HRRL Emit Test July Run Converting pixels to length 4.png 90 60
HRRL Emit Test July Run Converting pixels to length 5.png 90 59
HRRL Emit Test July Run Converting pixels to length 6.png 91 60
HRRL Emit Test July Run Converting pixels to length 7.png 90 60
Average Horizontal Diameter (pixels) Average Vertical Diameter (pixels)
[math] 90.29 \pm 0.49 [/math] [math] 59.43 \pm 0.53 [/math]
Horizontal mm/pixels Vertical mm/pixels
[math] 0.1108 \pm 0.0006 [/math] [math] 0.1683 \pm 0.0015 [/math]

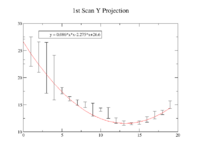
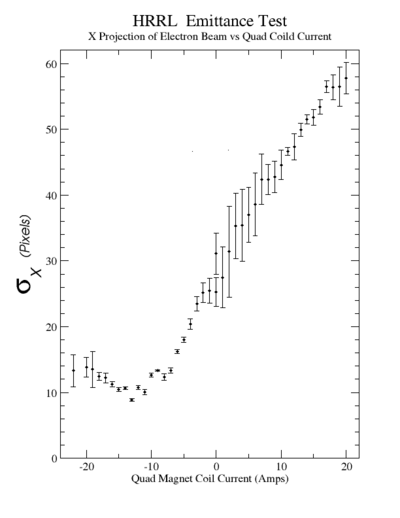
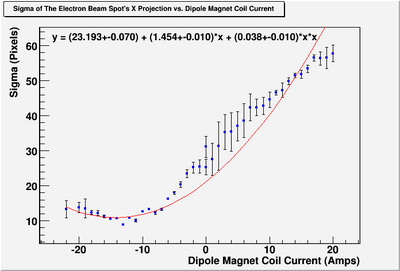
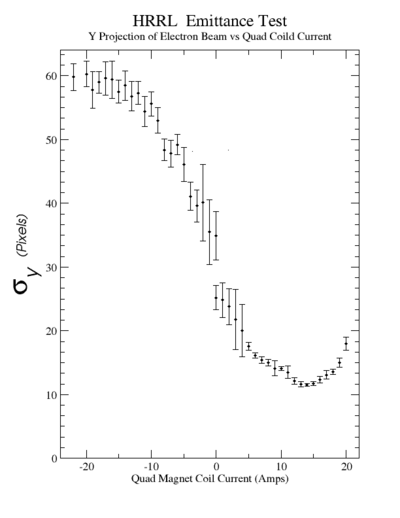
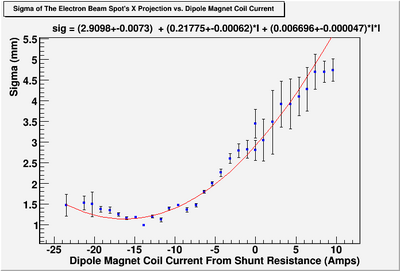
Sigma (in mm) vs Dipole Coil Current (on Shunt Resistance)

X Projection

Sigma inmm vs Dipole Coil Current onShunt with Fit for Projection X.png

The fit is:

[math] \sigma_x = (2.9098 \pm 0.0073) + (0.21775 \pm 0.00062)I + (0.006696 \pm 0.000047)I^{2} [/math]

p-value is less than 0.000001

For a parabola [math] y = a + bx + cx^{2} [/math], the [math] x [/math] corresponding to the minimum [math] y_{min} [/math] is:

[math] x_{min} = - \frac{b}{2c} [/math].

So, [math] I_{min} = -16.259707[/math]

and

[math] \Delta I_{min} = \sqrt{ \frac{(\Delta b)^2}{4c^2} + \frac{ b^2 (\Delta c)^2}{4c^4} } [/math].

[math] \Delta I_{x,min} = \sqrt{ \frac{(0.00062)^2}{4 \times (0.006696)^2} + \frac{ (0.21775)^2 \times (0.000047)^2}{4 \times (0.006696)^4} } = 0.123161 = 0.12[/math].


[math] I_{min} = -16.26 \pm 0.12 [/math].


[math] \sigma_{x,min} = 2.93671995816274 [/math]

[math] \sigma_{x,min, up} = 2.94409703114234 [/math]

[math] \sigma_{x,min, dn} = 2.92934288518313 [/math]


[math] \sigma_{x,min,up} - \sigma_{x,min} = 0.007377072979601 [/math]

[math] \sigma_{x,min} - \sigma_{x,min,dn}= 0.00737707297960144 [/math]


So,

[math] \sigma_{x,min} = 2.9367 \pm 0.0074 [/math]

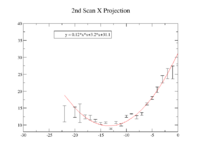
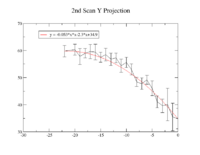
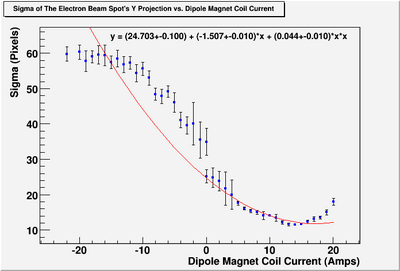
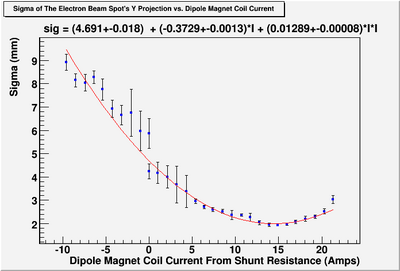
Y Projection

Sigma inmm vs Dipole Coil Current onShunt with Fit for Projection Y.png

The fit is:

[math] \sigma_{y} = (4.691 \pm 0.018) + (-0.3729 \pm 0.0013)I + (0.01289 \pm 0.00008)I^{2} [/math]

p-value is less than 0.000001

[math] x_{min} = - \frac{b}{2c} [/math].

So, [math] I_{min} = 14.464701[/math]

[math] \Delta I_{min} = \sqrt{ \frac{(\Delta b)^2}{4c^2} + \frac{ b^2 (\Delta c)^2}{4c^4} } [/math].

[math] \Delta I_{min} = \sqrt{ \frac{(0.0013)^2}{4 \times (0.01289) ^2} + \frac{ (-0.3729)^2 \times (0.00008)^2}{4 \times (0.01289)^4} } = 0.102966 [/math]


[math] I_{min} = 14.46 \pm 0.10 [/math].

[math] \sigma_{y,min} = 4.65274050365148 [/math]

[math] \sigma_{y,min, up} = 4.67087520809017 [/math]

[math] \sigma_{y,min, dn} = 4.63487351175864 [/math]


[math] \sigma_{y,min, up} - \sigma_{y,min} = 0.0181347044386939 [/math]

[math] \sigma_{y,min} - \sigma_{y,min, dn}= 0.0178669918928378 [/math]


So,

[math] \sigma_{y,min} = 4.653 \pm 0.018 [/math]


Conclusions

For X projection: [math] I_{x,min} = -16.26 \pm 0.12[/math], and [math] \sigma_{x,min} = 2.9367 \pm 0.0074 [/math]


For X projection: [math] I_{y,min} = 14.46 \pm 0.10 [/math], and [math] \sigma_{y,min} = 4.653 \pm 0.018 [/math]

Emittance

Quadrupole Strength: [math] k = 0.2998 \frac{g[T/m]}{p[GeV]} [/math]

g here is the gradient of the qudrupole. p is the momentum of the e- beam.

In our case, energy of the beam is 0.01 GeV and gap between dipole center and pole face is 1 inch.

[math] k = 0.2998 \frac{\frac{B(I)}{(1 inch)\times\frac{1 m}{1 inch}}[T/m]}{0.01 GeV} [/math]

[math]B(I) = (3.6 \pm 1.3) \times 10^{-3} + (1945 \pm 2) \times 10^{-5} I [kG] = (3.6 \pm 1.3) \times 10^{-4} + (1945 \pm 2) \times 10^{-6} I [T] [/math]

So,

[math] k = 0.2998 \frac{ (3.6 \pm 1.3) \times 10^{-4} + (1945 \pm 2) \times 10^{-6} I [T] }{0.01 \times 0.0254 [GeV][m]} [/math]

[math] k = (0.42 \pm 0.16) + (2.2956 \pm 0.0024) \times I[/math]


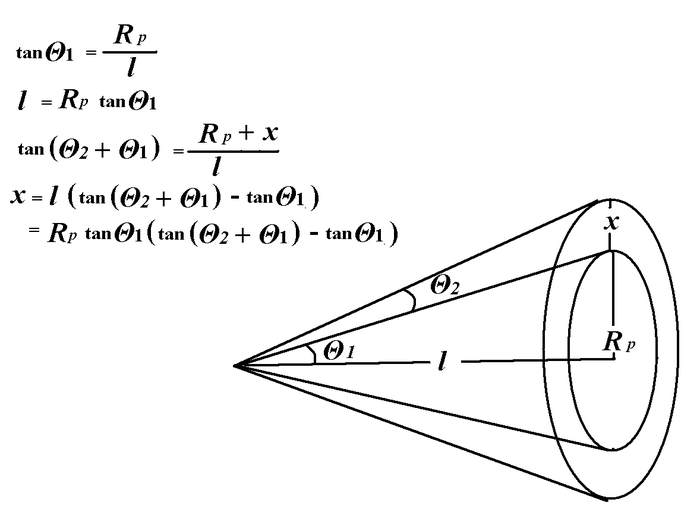
According to File:Emit Meas DAFNE Linac e Beam.pdf, for the case of quadruple scanning one quadrupole and screen, the emittance related to the quadrupole strength.

Transfer Matrix for 1uaruople \tilde{Q} and screen (drift space?) \tilde{S} consist the transfer matrix of the whole system as:

[math] \tilde{M} = \tilde{S}\tilde{Q} [/math]

[math] \tilde{Q} = \begin{bmatrix} 1 & 0 \\ k=\pm\frac{1}{f} & 1 \end{bmatrix}. [/math]

[math] \tilde{S} = \begin{bmatrix} S_{11} & S_{12} \\ S_{21} & S_{22} \end{bmatrix}. [/math]

[math] \sigma_{screen11} = Ak^2 - 2ABk + (C + AB^2) [/math]

[math] \epsilon = \frac{\sqrt{AC}}{S^2_{12}} [/math]

[math] S_{12} [/math] is the distance between quadrupole and screen.

If I have a fit:

[math] \sigma_{screen11} = xk^2 + yk + z [/math]

Then, [math] A=x, B=\frac{y}{-2A}, C=z-AB^2[/math]

Two fits are:

Sigma vs QuadStrength with Fit Projection X.png

Sigma vs QuadStrength with Fit Projection Y.png


Dr. Kim's Suggestion in his email

from	Yujong Kim <yjkim@isu.edu>
to	Sadiq Setiniyaz <sadik82@gmail.com>
cc	Dr Forest <tforest@athena.physics.isu.edu>
date	Fri, Oct 8, 2010 at 6:44 AM
subject	Re: Quad Scan Parameters

Dear Sadiq,

Many thanks,

I re-checked your QM scan fitting plot (final plots on emittance mewasurement).

Your fitting range too wide (-20 < k < 50).

Please fit again with a narrower range (+10 < k < 50).
Then, you can get much beautiful results.
Normally, we fit for only one k sign (positive or negative).
Yujong Kim


Here are results after doing Dr. Kim's suggested fit. 

Note: I also corrected the distance S12 to the distance between quad center and screen (I originally did from the end of the quad to the screen, this is wrong).

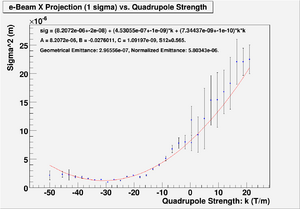
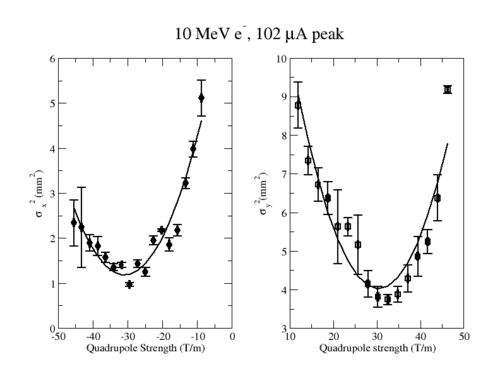
For X projection

HRRL Emit Parbola Fit Xaxis as BfieldStrength DrKimSugFit.png

Minimum ChiSqrd is: 129.749

The fit is:

sig^2 = (7.82463e-06+-2e-08) + (4.23945e-07+-1e-09)*k + (6.82167e-09+-1e-10)*k*k

Probability of obtaining data at least as incompatible with distribution as the data actually observed is 0.000000 A = 7.82463e-06, B = -0.0270904, C = 1.07925e-09, S12=0.64. Geometrical Emittance: 2.24354e-07 (m*rad), Normalized Emittance: 4.39048e-06 (m*rad).


Data file contains: Number-of-points B-Field-Strength Error-on-B-Field-Strength Sigma^2 Error-on-Sigma^2

File:HRRL Emit Parbola Fit Xaxis as BfieldStrength.txt


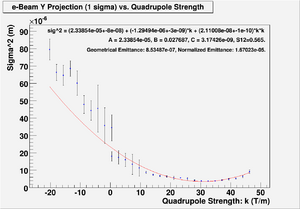
For Y projection

HRRL Emit Parbola Fit Yaxis as BfieldStrength DrKimSugFit.png

Minimum ChiSqrd is: 25.3174

The fit is:

sig^2 = (1.71755e-05+-8e-08) + (-8.38108e-07+-3e-09)*k + (1.3229e-08+-1e-10)*k*k

Probability of obtaining data at least as incompatible with distribution as the data actually observed is 0.000000 A = 1.71755e-05, B = 0.0243983, C = 3.00479e-09, S12=0.64. Geometrical Emittance: 5.54629e-07 (m*rad), Normalized Emittance: 1.08538e-05 (m*rad).

Data file contains: Number-of-points B-Field-Strength Error-on-B-Field-Strength Sigma Error-on-Sigma

File:HRRL Emit Parbola Fit Yaxis as BfieldStrength.txt

Data ROOTSYS Fit Script

File:ROOTSCRIPT for HRRL Emittace.C

Emittance Results for HRRL at 10 MeV and 102 micro Amp peak

Emittance HRRL 1mA.png
Measurements of the beam spot size as a function of the quadrupole magnetic field used to calculate the beam emittance. The fits are

[math]\sigma^2_x = (7.824\pm 0.02) + (0.424 \pm 0.001)k + (6.8 \pm 0.1 \times 10^{-9} )k^2[/math] and [math]\sigma^2_y =17.17 \pm 0.08) - (0.084 \pm 0.003)k + (13.2 \pm 0.1e-10 \times 10^{-9}) k^2[/math] with a[math] \chi^2/\nu[/math] of 8.1 and 1.7 respectively. The respective P-values for this fit are 0.05 and 10^{-20}.

File:Emmitance HRRL 1mA 10-14-10.xmgrace.txt

Automatic Script to plot RMS

ROOT

How does the fit look when using the script below.

Working on it.

You should do background subtraction instead of cutting out the spot.

 2 bugs remain till Spe 24th. 1. entries; 2. Sub->Draw();

Running Parabola_Fit_for_AutoRMS.C will run AutoRMS.C and do the fits.


File:AutoRMS.C


File:Parabola Fit for AutoRMS.C

This 2 programs and pictures for data can be downloaded at: [2]

MATLAB

These MATLAB scripts will do Gaussian fits for beam spots and get rms beam size on x and projections (by Gauss_Fit.m). These rms values will be passed on (to Emit_Parabola_Fit_kl_YProjection.m and Emit_Parabola_Fit_kl_YProjection.m) to fit parabola. Parabola fit will be plotted,and emittances, normalized emittances, beta functions, alpha functions will given at the end.

File:Get Emittance.rar

File:Guass Fit.txt

File:Emit Parabola Fit kl XProjection.txt

File:Emit Parabola Fit kl YProjection.txt

File:Gauss.txt

File:Gausschisq.txt

File:Gaussfit.txt

File:Plot Beam Spot.txt

File:Plot Gauss Fit.txt

File:ReadMe.txt

Alternative Analysis from the East Cost

Image Analysis

Emittance/TWISS parameter extraction


New Fits with K1L

No Fringe Field Effect

We want to do new fits with K1L. K1 is quadrupole strength and L is the thickness of the quadrupole. We will do it for the data we got previously. They are the following two data sets.

At this step, we will ignore fringe field effect, we want to consider it later. 


need uncertainties in plots below

The uncertainties are difficult to believe because they are so small (< 0.1% !)

Redo you plots so they look like the ones below in terms of line boldness and quality.  Identify the fit parameters and their error as well as a measurement of the goodness of fit.

https://wiki.iac.isu.edu/index.php/File:Emittance_HRRL_1mA.png


Data files contains:

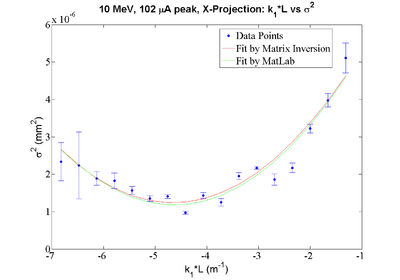
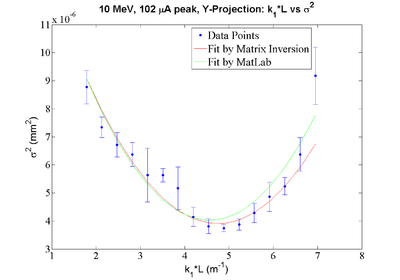
Number-of-points B-Field-Strength Error-on-B-Field-Strength Sigma^2 Error-on-Sigma^2


File:HRRL Emit Parbola Fit Xaxis as BfieldStrength.txt

File:HRRL Emit Parbola Fit Yaxis as BfieldStrength.txt 

X-Projection:
Fit Parameters by MATLAB:
y = 0.00000784 + (0.00000288)*x + 0.00000031*x*x
Fit Parameters by Matrix Inversion:
y = (0.00000781+-0.00000027) + (0.00000282+-0.00000014)*x + (0.00000030+-0.00000002)*x*x
P-value = 7.6238e-21

Y-Projection:
Fit Parameters by MATLAB:
y = 0.00001766 + (-0.00000599)*x + 0.00000066*x*x
Fit Parameters by Matrix Inversion:
y = (0.00001717+-0.00000084) + (-0.00000558+-0.00000041)*x + (0.00000059+-0.00000005)*x*x
P-value =  0.020964

geometrical emittance:    [math]\epsilon_{x}  =   1.5   \pm  1.4  ~ mm*mrad[/math]     [math]\epsilon_{y} =  3.7 \pm 3.9  ~ mm*mrad [/math]
normalized emittance:     [math]\epsilon_{n,x}  =  29    \pm   27 ~ mm*mrad[/math]     [math]\epsilon_{n,y} = 72.0 \pm  77.0 ~ mm*mrad [/math]
                          [math]\beta_{x} = 0.49  \pm 0.23  [/math]                    [math]\beta_{y} = 0.39 \pm 0.16  [/math]
                          [math]\alpha_{x} = -1.53   \pm  0.72 [/math]                 [math]\alpha_{y} = 2.5  \pm 1.0 [/math]




X Projection:

HRRL Emit New Fits with K1L X Projection withErr.png


Y Projection:

HRRL Emit New Fits with K1L Y Projection withErr.png





Corrections for vertical calibration

We made error when we are doing vertical calibration. When we calculate vertical calibration, we need to multiply the diameter of the circle by [math] cos45^{o} [/math].

This is the reason that we got dramatically different results in vertical and horizontal emittances.


Errors in Converting pixels to length for Vertical

Average Horizontal Diameter (pixels) Average Vertical Diameter (pixels)
[math] 90.29 \pm 0.49 [/math] [math] 59.43 \pm 0.53 [/math]
Horizontal mm/pixels Vertical mm/pixels
[math] 0.1108 \pm 0.0006 [/math] [math] 0.1683 \pm 0.0015 [/math]
[math] V_{cal} [/math] need to be multiplied by [math] cos45^{o} [/math]
[math] 0.1190\pm 0.0011 [/math]

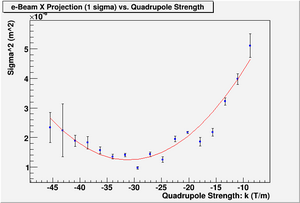
New Fits with K1L

Considering fringe field effect with "Cheap and Dirty" way

X Projection

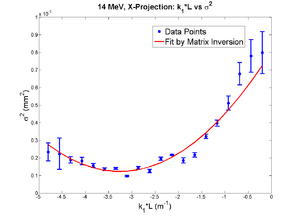
HRRL Emitt 2010 Jul Refit After Correcting Calibration Projection X.png

x-projection:

emit=2.2 +- 1.3 mm*mrad, emit_norm=42.4 +- 25.4 mm*mrad

beta=0.72 +- 0.31, alpha=-1.23 +-0.56 

//K1*L(1/m)   er K1*L    sgima^2(mm)   er sigma^2

Media:2010_Jul_Emit_refit_data_x.txt


parabola fit for x-projection (y in mm unit):

y = (8.05126 +-0.24983) + (4.18341+-0.18968)*x + (0.64143+-0.03472)*x.*x

Data created from parabola fit

Media:2010_Jul_Emit_data_from_fit_x.txt

Y Projection

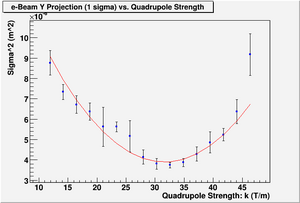
HRRL Emitt 2010 Jul Refit After Correcting Calibration Projection Y.png


y-projection:

emit=2.6 +- 2.0 mm*mrad, emit_norm=50.5 +- 38.3 mm*mrad

beta=0.54 +- 0.22, alpha=2.68 +-1.13 


//K1*L(1/m)   er K1*L    sgima^2(mm)   er sigma^2

Media:2010_Jul_Emit_refit_data_y.txt


parabola fit for y-projection (y in mm unit):

y = (8.51813 +-0.40098) + (-3.88142+-0.28132)*x + (0.57350+-0.04792)*x.*x

Data created from parabola fit

Media:2010_Jul_Emit_data_from_par_fit_y.txt


Go back Positrons

Retrieved from "https://wiki.iac.isu.edu/index.php?title=Emittance_Test&oldid=78587"