Difference between revisions of "Integrated asymmetry"
Jump to navigation
Jump to search
| (87 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | [ | + | [https://wiki.iac.isu.edu/index.php/Roman_calculation Go Back] |
=Integrated asymmetry calculation= | =Integrated asymmetry calculation= | ||
| − | <math>Asymm^{detA} = \frac{\left(\frac{up}{ | + | <math>Asymm^{detA,detC} = \frac |
| − | + | {\left(\frac{N_{up}^{D_2O}}{W_{up}^{D_2O}}-\frac{N_{up}^{H_2O}}{W_{up}^{H_2O}}\right) | |
| − | + | - \left(\frac{N_{side}^{D_2O}}{W_{sided}^{D_2O}}-\frac{N_{side}^{H_2O}}{W_{sd}^{H_2O}}\right)} | |
| − | + | {\left(\frac{N_{up}^{D_2O}}{W_{up}^{D_2O}}-\frac{N_{up}^{H_2O}}{W_{up}^{H_2O}}\right) | |
| − | + | + \left(\frac{N_{side}^{D_2O}}{W_{sd}^{D_2O}}-\frac{N_{sided}^{H_2O}}{W_{sd}^{H_2O}}\right)} | |
| + | </math><br><br> | ||
where<br> | where<br> | ||
| − | <math> | + | <math>N_{k}^{m}=\sum_{ii=min}^{max}{count(ii)};</math> total number of neutrons detected, k = [Up,Side], m = [D2O, H2O]<br> |
| − | + | <math>W_{k}^{m};</math> weighted (NaI, Ref) coefficient, k = [Up,Side], m = [D2O, H2O] <br> | |
| − | |||
| − | |||
| − | <math> | ||
| − | |||
| − | |||
| − | |||
*For detector A summation is over [1000:1600] bin numbers<br> | *For detector A summation is over [1000:1600] bin numbers<br> | ||
| Line 22: | Line 17: | ||
=Error calculation= | =Error calculation= | ||
| − | <math> | + | <math>\delta (Asymm) = |
| − | + | \sqrt{\sum_{k=up}^{side}\ \sum_{m=D_2O}^{H_2O} | |
| + | \left[\left(\frac{\partial A}{\partial N_{k}^{m}}\delta N_{k}^{m}\right)^2 + | ||
| + | \left(\frac{\partial A}{\partial W_{k}^{m}}\delta W_{k}^{m}\right)^2\right]}</math> | ||
| + | |||
| + | What about | ||
| + | |||
| + | <math>\frac{\partial A}{\partial N_{k}^{m}}\frac{\partial A}{\partial W_{k}^{m}}</math> | ||
| + | |||
| + | <pre> | ||
| + | what is <math>\sqrt{up}</math> ? | ||
| + | Does <math>\sqrt{up}</math> = number of counts in in the detector | ||
| + | up spectrum as suggested above? Why not use <math>N_{up}</math> as variable. | ||
| + | If distribution is Binomial (detector yes/no) then width of distribution is | ||
| + | <math>1.265\sqrt{N}</math> = 2 times e error. | ||
| + | Relative error = <math>\frac{error}{Ave} = \frac{0.6325 \sqrt{N}}{N/2}</math> | ||
| + | |||
| + | If you are measuring total number of neutrons detected then you will have binomial if you | ||
| + | break up the time spectrum into bins and don't integrate then probability distribution | ||
| + | is combination of detection probability and time measurement probability. | ||
| + | </pre> | ||
| + | |||
| + | If we take:<br> | ||
| + | <math>\delta N_{k}^{m} = \sqrt{N_{k}^{m}}</math><br> | ||
| + | <math>\delta W_{k}^{m} = \sqrt{N_{k}^{m}}</math><br><br> | ||
| + | |||
| + | then<br> | ||
| + | <math>\delta (Asymm) = | ||
| + | \sqrt{ | ||
| + | \left(\frac{(+)-(-)}{(+)^2}\right)^2\left( | ||
| + | \frac{N_{up}^{D_2O}}{(W_{up}^{D_2O})^2}+\frac{(N_{up}^{D_2O})^2}{W_{up}^{D_2O}} | ||
| + | +\frac{N_{up}^{H_2O}}{(W_{up}^{H_2O})^2}+\frac{(N_{up}^{H_2O})^2}{W_{up}^{H_2O}}\right)+ | ||
| + | \left(\frac{(+)+(-)}{(+)^2}\right)^2\left( | ||
| + | \frac{N_{sd}^{D_2O}}{(W_{sd}^{D_2O})^2}+\frac{(N_{sd}^{D_2O})^2}{W_{sd}^{D_2O}} | ||
| + | +\frac{N_{sd}^{H_2O}}{(W_{sd}^{H_2O})^2}+\frac{(N_{sd}^{H_2O})^2}{W_{sd}^{H_2O}}\right)}</math><br><br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
where<br> | where<br> | ||
| − | <math>(-)=\left[\left(\frac{up}{ | + | <math>(-)=\left[ |
| − | <br> | + | \left(\frac{N_{up}^{D_2O}}{W_{up}^{D_2O}}-\frac{N_{up}^{H_2O}}{W_{up}^{H_2O}}\right) |
| − | <math>( | + | -\left(\frac{N_{sd}^{D_2O}}{W_{sd}^{D_2O}}-\frac{N_{sd}^{H_2O}}{W_{sd}^{H_2O}}\right)\right]</math> |
| − | <br> | + | <br><br> |
| − | + | <math>(-)=\left[ | |
| + | \left(\frac{N_{up}^{D_2O}}{W_{up}^{D_2O}}-\frac{N_{up}^{H_2O}}{W_{up}^{H_2O}}\right) | ||
| + | +\left(\frac{N_{sd}^{D_2O}}{W_{sd}^{D_2O}}-\frac{N_{sd}^{H_2O}}{W_{sd}^{H_2O}}\right)\right]</math><br><br> | ||
| + | |||
=Cases was analysed= | =Cases was analysed= | ||
Det A (was analized all possible combination): | Det A (was analized all possible combination): | ||
| − | D2O Up, files# [40,56,102,108 | + | D2O Up, files# [40,56,102,108,205,210,230];<br> |
H2O Up, files# [44];<br> | H2O Up, files# [44];<br> | ||
| − | D2O Side, files# [48,74,78,82,86,90,94,146 | + | D2O Side, files# [48,74,78,82,86,90,94,146,190,225,235];<br> |
H2O Side, files# [52];<br> | H2O Side, files# [52];<br> | ||
Det C (was analized all possible combination): | Det C (was analized all possible combination): | ||
| − | D2O Up, files# [49,75,79,83,87,91,95,147 | + | D2O Up, files# [49,75,79,83,87,91,95,147,191,226,236];<br> |
H2O Up, files# [53];<br> | H2O Up, files# [53];<br> | ||
| − | D2O Side, files# [41,57,103,107 | + | D2O Side, files# [41,57,103,107,206,211,231];<br> |
H2O Side, files# [45];<br><br> | H2O Side, files# [45];<br><br> | ||
| + | |||
| + | =Weighted coefficients was used= | ||
| + | ([[Image:Weight_coeff.pdf ]])<br><br> | ||
=Results= | =Results= | ||
| Line 53: | Line 82: | ||
Table 3: Det A, weighted with <math>{\color{Red}Ref \ detector}</math><br> | Table 3: Det A, weighted with <math>{\color{Red}Ref \ detector}</math><br> | ||
Table 4: Det C, weighted with <math>{\color{Red}Ref \ detector}</math><br><br><br> | Table 4: Det C, weighted with <math>{\color{Red}Ref \ detector}</math><br><br><br> | ||
| − | ([[Image: | + | ([[Image:Asymm_table.pdf]])<br><br> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
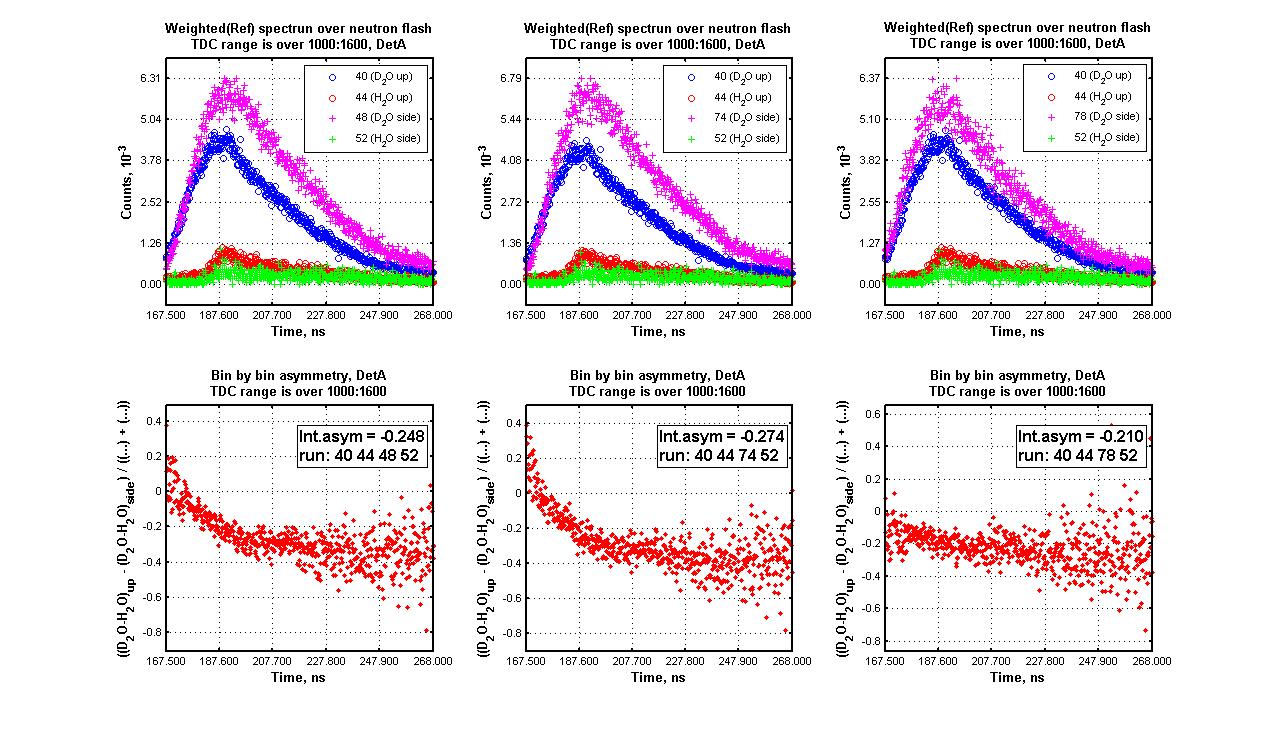
=Example of bin by bin asymmetry= | =Example of bin by bin asymmetry= | ||
| − | [[Image:Asymm_RefDet_DetA_40,44,48(74,78),52.jpg]] | + | Change the X-axis to nanosecond or neutron energy (TF). A:Have done. |
| + | [[Image:Asymm_RefDet_DetA_40,44,48(74,78),52.jpg]]<br><br> | ||
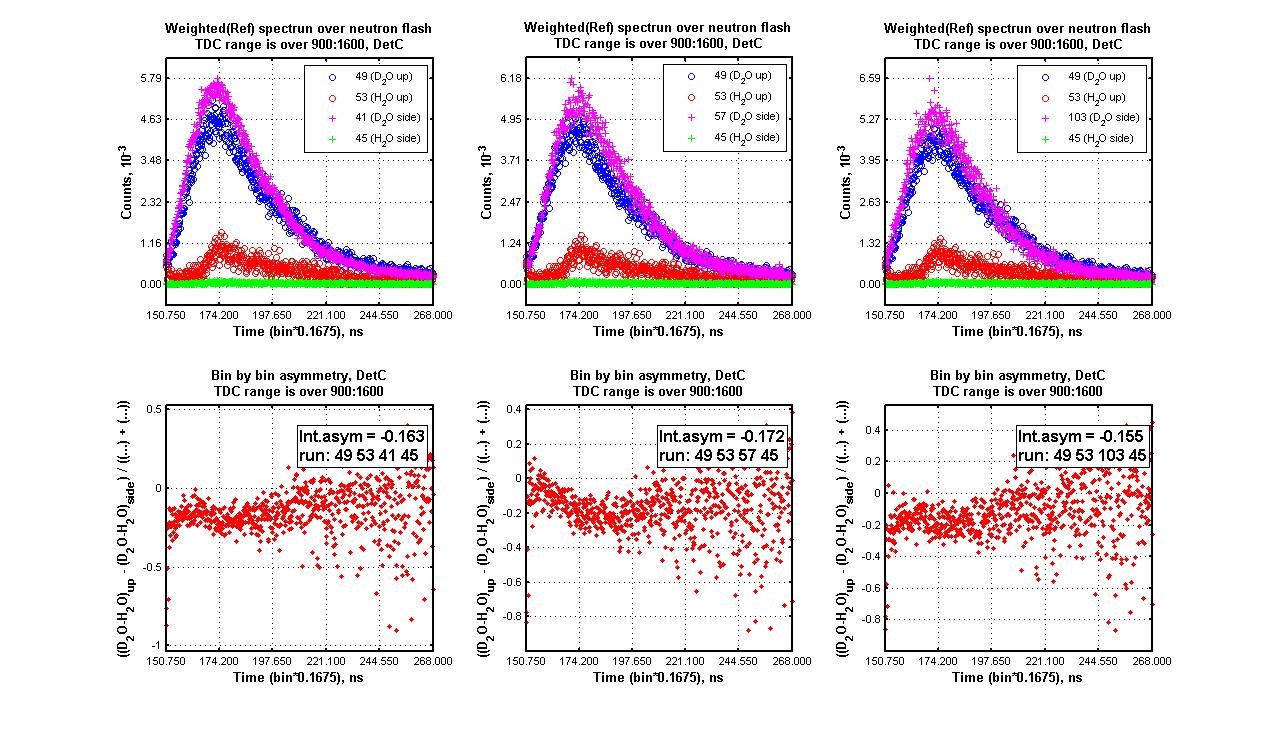
| + | [[Image:Asymm_RefDet_DetC_49,53,41(57,103),45.jpg]] | ||
[http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | [http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | ||
Latest revision as of 19:02, 24 May 2012
Integrated asymmetry calculation
where
total number of neutrons detected, k = [Up,Side], m = [D2O, H2O]
weighted (NaI, Ref) coefficient, k = [Up,Side], m = [D2O, H2O]
- For detector A summation is over [1000:1600] bin numbers
- For detector C summation is over [900:1600] bin numbers
Error calculation
What about
what is <math>\sqrt{up}</math> ?
Does <math>\sqrt{up}</math> = number of counts in in the detector
up spectrum as suggested above? Why not use <math>N_{up}</math> as variable.
If distribution is Binomial (detector yes/no) then width of distribution is
<math>1.265\sqrt{N}</math> = 2 times e error.
Relative error = <math>\frac{error}{Ave} = \frac{0.6325 \sqrt{N}}{N/2}</math>
If you are measuring total number of neutrons detected then you will have binomial if you
break up the time spectrum into bins and don't integrate then probability distribution
is combination of detection probability and time measurement probability.
If we take:
then
where
Cases was analysed
Det A (was analized all possible combination):
D2O Up, files# [40,56,102,108,205,210,230];
H2O Up, files# [44];
D2O Side, files# [48,74,78,82,86,90,94,146,190,225,235];
H2O Side, files# [52];
Det C (was analized all possible combination):
D2O Up, files# [49,75,79,83,87,91,95,147,191,226,236];
H2O Up, files# [53];
D2O Side, files# [41,57,103,107,206,211,231];
H2O Side, files# [45];
Weighted coefficients was used
Results
Table 1: Det A, weighted with
Table 2: Det C, weighted with
Table 3: Det A, weighted with
Table 4: Det C, weighted with
Example of bin by bin asymmetry
Change the X-axis to nanosecond or neutron energy (TF). A:Have done.