|
|
| (12 intermediate revisions by the same user not shown) |
| Line 308: |
Line 308: |
| | | | |
| | ====== Phi rate ====== | | ====== Phi rate ====== |
| − | =======1.6 < Q^2 < 1.9 =======
| |
| − | {|border="2" colspan = "20"
| |
| − | !Run Number||S1||S2 || S3||S4 ||S5 || S6 || all sectors
| |
| − | |-
| |
| − | | || || || || || || ||
| |
| − | |-
| |
| − | |}
| |
| − |
| |
| − |
| |
| − | It is not weighted.<br>
| |
| − | [[Image:good_phi_angle_in_cm_frame_i_think.gif|600px]]<br>
| |
| − | <math>\phi</math> angle in cm frame should be between -90 and +90, because tanget is periodic function.<br>
| |
| − |
| |
| − | [[Image:phi_angle_in_cm_frame_without_cuts_for_the_following_files_27070_27072_27073_27074_27095_05.gif|600px]]<br>
| |
| − | [[Image:phi_angle_in_cm_frame_with_cut_Q_for_the_following_files_27070_27072_27073_27074_27095_05.gif|600px]]<br>
| |
| − |
| |
| − |
| |
| − | [[Image:phi_angle_in_cm_frame_without_cuts_for_the_following_files_27070_27072_27073_27074_27095_05_1.gif|600px]]<br>
| |
| − | [[Image:phi_angle_in_cm_frame_with_cut_Q_for_the_following_files_27070_27072_27073_27074_27095_05_1.gif|600px]]<br>
| |
| | | | |
| | {|border="2" colspan = "4" | | {|border="2" colspan = "4" |
| Line 336: |
Line 317: |
| | | | |
| | [http://iac.isu.edu/mediawiki/index.php/Phi_angle_in_CM_frame_for_different_runs phi angle in cm frame for different runs]<br> | | [http://iac.isu.edu/mediawiki/index.php/Phi_angle_in_CM_frame_for_different_runs phi angle in cm frame for different runs]<br> |
| | + | |
| | + | |
| | | | |
| | start calculating cross -section | | start calculating cross -section |
| | | | |
| − | ;Luminosity Calculation for NH3(Ammonia) target
| + | ======Luminosity Calculation for NH3(Ammonia) target ====== |
| | | | |
| | The target materials are located in the target cells. They are made out of polychlorotrifluoroethylene with a thickness of 0.2 mm. The cells itself are in diameter 15 (15.7) mm and in length 10 (12.7) mm, with 0.025 mm aluminum entrance windows and 0.05 mm kapton exit windows. [http://books.google.com/books?id=LEqA4cMrkfIC&pg=PA329&lpg=PA329&dq=target+NH3,+CLAS,+luminosity&source=web&ots=yWZHoDjDDI&sig=yW0oVF1zIQgJZ5yqAMElflnhxsY&hl=en#PPA329,M1] | | The target materials are located in the target cells. They are made out of polychlorotrifluoroethylene with a thickness of 0.2 mm. The cells itself are in diameter 15 (15.7) mm and in length 10 (12.7) mm, with 0.025 mm aluminum entrance windows and 0.05 mm kapton exit windows. [http://books.google.com/books?id=LEqA4cMrkfIC&pg=PA329&lpg=PA329&dq=target+NH3,+CLAS,+luminosity&source=web&ots=yWZHoDjDDI&sig=yW0oVF1zIQgJZ5yqAMElflnhxsY&hl=en#PPA329,M1] |
| | + | |
| | + | [[Media:fill.factor.ps]] NH3 Filling Factor Evaluation, R. De Vita, July 1999<br> |
| | | | |
| | :<math>L = \frac{i_{scattered}}{\sigma} \sim i_{beam} \rho_{target} l_{target}</math> | | :<math>L = \frac{i_{scattered}}{\sigma} \sim i_{beam} \rho_{target} l_{target}</math> |
| Line 367: |
Line 352: |
| | ::<math> L = 1.288 \times 10^{33} \frac{1572}{309 \times 6} \frac{[ \# of electrons]}{second \times cm^2} =</math> | | ::<math> L = 1.288 \times 10^{33} \frac{1572}{309 \times 6} \frac{[ \# of electrons]}{second \times cm^2} =</math> |
| | ::<math>= 1.09209 \times 10^{33} \frac{[ \# of electrons]}{second \times cm^2}</math><br> | | ::<math>= 1.09209 \times 10^{33} \frac{[ \# of electrons]}{second \times cm^2}</math><br> |
| | + | |
| | + | ::<math>= 1.09209 \times 30 \times 10^{33} \frac{[ \# of electrons]}{cm^2} = 3.3 \times 10^{34} \frac{[ \# of electrons]}{cm^2}</math><br> |
| | | | |
| | The luminosity of the continuous electron beam was <math>10^{34}</math> <math>cm^{-2} sec^{-1}</math> [http://arxiv.org/abs/0709.1946v2] [http://books.google.com/books?id=LEqA4cMrkfIC&pg=PA329&lpg=PA329&dq=target+NH3,+CLAS,+luminosity&source=web&ots=yWZHoDjDDI&sig=yW0oVF1zIQgJZ5yqAMElflnhxsY&hl=en#PPA329,M1]<br> | | The luminosity of the continuous electron beam was <math>10^{34}</math> <math>cm^{-2} sec^{-1}</math> [http://arxiv.org/abs/0709.1946v2] [http://books.google.com/books?id=LEqA4cMrkfIC&pg=PA329&lpg=PA329&dq=target+NH3,+CLAS,+luminosity&source=web&ots=yWZHoDjDDI&sig=yW0oVF1zIQgJZ5yqAMElflnhxsY&hl=en#PPA329,M1]<br> |
| − |
| |
| − | why are we a factor of 2 different from reference 8 above? Ref 8 says at 4 nA L = 15 x 10^{33}. The above says 1 x 10 ^{33} when I=6 nA.<br>
| |
| − |
| |
| | | | |
| | ;Cross Section Calculation | | ;Cross Section Calculation |
| | | | |
| | + | [[Media:cross_sections_1.pdf]]<br> |
| | + | |
| | : <math>\frac{d\sigma}{d\Omega} = \frac{1}{L} \frac{d^{2}N}{d\Omega dt}</math><br> | | : <math>\frac{d\sigma}{d\Omega} = \frac{1}{L} \frac{d^{2}N}{d\Omega dt}</math><br> |
| | where<br> | | where<br> |
Quality Checks
Run Summary Table
The table below uses a characteristic DST file to try and estimate the sample size for a semi-inclusive analysis of pion electroproduction. The column marked "cuts" below indicates the number of events kept when the standard EC based electron identification cuts, described above, are used: [math]EC_{tot}\gt 0.2*p [/math] and
[math] EC_{inner}\gt 0.08*p[/math]. The next step will be to compare unpolarized pion production rates in order to evaluate the CLAS detectors efficiencies for measuring charged pions with different torus polarities. The question is whether you get the same rates for negatively charged pions in one torus polarity to positively charged pions using the opposite torus polarity.
| Beam Energy |
Torus Current |
Target |
Begin Run |
End Run |
file used |
# trig([math]10^6[/math]) |
events remaining after [math]e^-[/math] cuts(%) |
expected # evts([math]10^6[/math]) |
events remaining after [math]e^-[/math] and [math]\pi^+[/math] cuts(%) |
expected # evts([math]10^6[/math]) |
events remaining after [math]e^-[/math] and [math]\pi^-[/math] cuts(%) |
expected # evts([math]10^6[/math])
|
| 4239 |
2250 |
NH3 |
28205 |
28277 |
/cache/mss/home/nguler/dst/dst28205_05.B00 |
1108.72 |
60.8 |
674.1 |
8.3 |
92.02 |
3.24 |
35.92
|
|
|
ND3 |
28074 |
28190 |
/cache/mss/home/nguler/dst/dst28187_05.B00 |
1117.87 |
59.6 |
666.25 |
7.99 |
89.32 |
3.3 |
36.9
|
|
-2250 |
NH3 |
28407 |
28479 |
/cache/mss/home/nguler/dst/dst28409_05.B00 |
1013.57 |
24.2 |
245.28 |
0.12 |
1.22 |
0 |
0
|
|
|
ND3 |
28278 |
28403 |
/cache/mss/home/nguler/dst/dst28400_05.B00 |
1556.04 |
23.9 |
371.89 |
0.02 |
0.31 |
0.05 |
0.51
|
| 5735 |
2250 |
NH3 |
27074 |
27195 |
/cache/mss/home/nguler/dst/dst27095_05.B00 |
1442.25 |
57.7 |
832.18 |
9.3 |
134.13 |
3.8 |
59.13
|
|
|
ND3 |
27116 |
27170 |
/cache/mss/home/nguler/dst/dst27141_05.B00 |
624.55 |
59.1 |
369.10 |
9.53 |
59.52 |
3.9 |
24.36
|
|
-2250 |
NH3 |
26911 |
27015 |
/cache/mss/home/nguler/dst/dst26988_05.B00 |
900.93 |
80.7 |
727.05 |
7.14 |
64.33 |
9.9 |
89.19
|
|
|
ND3 |
27022 |
27068 |
/cache/mss/home/nguler/dst/dst27055_05.B00 |
711.53 |
80 |
569.22 |
6.97 |
49.59 |
10.1 |
71.86
|
Rates
Unpolarized Pion electroproduction
Rates from other experiments in our Kinematic range
Center of Mass Frame Transformation
We have proton and electron. In the Lab frame electron is moving along the x-axis with momentum ;[math]\vec{p_e}[/math] and proton is at rest. The 4-vectors are:
- Lab Frame
- [math]P_e=[/math]([math]E_e[/math],[math]p_e[/math],0,0) and for proton :[math]P_p=[/math]([math]m_p[/math],0,0,0)
- CM Frame
- :[math]{P_e}^{\prime}=[/math]([math]{E_e}^{\prime}[/math],[math]{p_e}^{\prime}[/math],[math]0[/math],[math]0[/math]) and for proton :[math]{P_p}^{\prime}=[/math]([math]{E_p}^{\prime}[/math],[math]{p_p}^{\prime}[/math],[math]0[/math],[math]0[/math])
- Find [math] \beta_{CM} [/math] such that [math]P_{tot}^{CM}=0 =p_e^{\prime} + {p_p}^{\prime}[/math]
- [math]\left ( \begin{matrix} {E_e}^{\prime} \\ p_e^{\prime} \\ 0 \\ 0 \end{matrix} \right )= \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 & 1 \end{matrix} \right ] \left ( \begin{matrix} E_e \\ p_e \\ 0 \\ 0 \end{matrix} \right )[/math]
- [math]\left ( \begin{matrix} {E_p}^{\prime} \\ p_p^{\prime} \\ 0 \\ 0 \end{matrix} \right )= \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} m_p \\ 0 \\ 0 \\ 0 \end{matrix} \right )[/math]
Using the last two equations we will get the following for x component:
- [math]{p_e}^{\prime}=-\gamma_{cm}(\beta_{cm} E_e-p_e)[/math]
- [math]p_p^{\prime} = - \gamma_{cm} \beta_{cm} m_p[/math]
- [math] \gamma_{cm}(p_e - \beta_{cm} E_e)= \gamma_{cm} \beta_{cm} m_p [/math]
- [math]\beta_{cm} = \frac {p_e}{m_p + E_e}[/math]
Example of the Missing Mass Calculation for the following reaction [math]e^- p^+ \rightarrow (e^-)^{\prime} \pi^{-} X [/math]
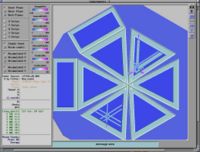
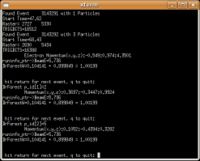
- [math]p_e = 5.736 Gev \sim E_e[/math] : electron mass is neglibible
- [math]m_p = 0.938 GeV[/math] : Mass of a proton
- [math]\beta_{cm} = \frac{5.736}{6.674} = 0.859 \lt 1[/math]
- [math]\gamma_{cm} = \frac{1}{\sqrt{1 - \beta_{cm}^2}} = \frac{1}{\sqrt{1 - 0.859^2}} = 1.9532[/math]
- [math]\left ( \begin{matrix} {E_e}^{\prime} \\ p_{ex}^{\prime} \\ p_{ey}^{\prime} \\ p_{ez}^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma_{cm} & 0 & 0 & -\gamma_{cm} \beta_{cm} \\ 0 & 1 &0 &0 \\ 0 &0 &1 &0 \\ -\gamma_{cm} \beta_{cm} &0 &0 &\gamma_{cm}\end{matrix} \right ] \left ( \begin{matrix} E_e=4.4915 \\ -0.549 \\ 0.974 \\ 4.3501 \end{matrix} \right )[/math]
- [math]\left ( \begin{matrix} {E_p}^{\prime} \\ p_{px}^{\prime} \\ p_{py}^{\prime} \\ p_{pz}^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma_{cm} & 0 & 0 & -\gamma_{cm} \beta_{cm} \\ 0 & 1 &0 &0 \\ 0 &0 &1 &0 \\ -\gamma_{cm} \beta_{cm} &0 &0 & \gamma_{cm} \end{matrix} \right ] \left ( \begin{matrix} E_p = 1.4563 \\ 0.3697 \\ -0.3447 \\ 0.9924 \end{matrix} \right )[/math]
- [math]\left ( \begin{matrix} {E_{\pi^-}}^{\prime} \\ p_{\pi^- x}^{\prime} \\ p_{{\pi^-} y}^{\prime} \\ p_{{\pi^-} z}^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma_{cm} & 0 & 0 & -\gamma_{cm} \beta_{cm} \\ 0 & 1 &0 &0 \\ 0 &0 &1 &0 \\ -\gamma_{cm} \beta_{cm} &0 &0 & \gamma_{cm} \end{matrix} \right ] \left ( \begin{matrix} E_{\pi^-} = 0.5757 \\ 0.1052 \\ -0.4394 \\ 0.3282 \end{matrix} \right )[/math]
- Electron
- [math]\left ( \begin{matrix} {E_e}^{\prime} \\ p_{ex}^{\prime} \\ p_{ey}^{\prime} \\ p_{ez}^{\prime} \end{matrix} \right )= \left ( \begin{matrix} 4.4915 \gamma_{cm} - 4.3501 \gamma_{cm} \beta_{cm} \\ -0.549 \\ 0.974 \\ -4.4915 \gamma_{cm} \beta_{cm} + 4.3501 \gamma_{cm} \end{matrix} \right ) = \left ( \begin{matrix} 1.4742 \\ -0.549 \\ 0.974 \\ 0.96078 \end{matrix} \right )[/math]
- Proton
- [math]\left ( \begin{matrix} {E_p}^{\prime} \\ p_{px}^{\prime} \\ p_{py}^{\prime} \\ p_{pz}^{\prime} \end{matrix} \right )= \left ( \begin{matrix} 1.4563\gamma_{cm} - 0.9924 \gamma_{cm} \beta_{cm} \\ 0.3697 \\ -0.3447 \\-1.4563 \gamma_{cm} \beta_{cm} + 0.9924\gamma_{cm} \end{matrix} \right ) = \left ( \begin{matrix} 1.17939 \\ 0.3697 \\ -0.3447 \\ -0.505023 \end{matrix} \right )[/math]
- [math]\pi^-[/math]
- [math]\left ( \begin{matrix} {E_{\pi^-}}^{\prime} \\ p_{\pi^- x}^{\prime} \\ p_{{\pi^-} y}^{\prime} \\ p_{{\pi^-} z}^{\prime} \end{matrix} \right )= \left ( \begin{matrix} 0.5757\gamma_{cm} - 0.3282 \gamma_{cm} \beta_{cm} \\ 0.1052 \\ -0.4394 \\ -0.5757 \gamma_{cm} \beta_{cm} + 0.3282\gamma_{cm} \end{matrix} \right ) = \left ( \begin{matrix} 0.5738 \\ 0.1052 \\ -0.4394 \\ -0.324868 \end{matrix} \right )[/math]
[math]\vec {P_{tot}}^{\prime} = (p_{ex}^{\prime} + p_{px}^{\prime} + p_{\pi^-x}^{\prime})\hat{x} + (p_{ey}^{\prime} + p_{py}^{\prime} + p_{\pi^-y}^{\prime})\hat{y} + (p_{ez}^{\prime} + p_{pz}^{\prime} + p_{\pi^-z}^{\prime})\hat{z} = - 0.0741 \hat{x} + 0.1899 \hat{y} + 0.13 \hat{z} [/math]
- Missing Mass
- Conservation of the 4-momentum gives us following
[math](P_e)^\mu + (P_p)^\mu = ({P_e}^{\prime})^\mu + ({P_X}^{\prime})^\mu + ({P_{\pi^-}}^{\prime})^\mu[/math]
[math](P_e)_\mu + (P_p)_\mu = ({P_e}^{\prime})_\mu + ({P_X}^{\prime})_\mu + ({P_{\pi^-}}^{\prime})_\mu[/math]
- Solving it for the final proton state
[math]{M_x}^2 = ({P_X}^{\prime})_\mu({P_X}^{\prime})^\mu = [(P_e)_\mu + (P_p)_\mu - ({P_e}^{\prime})_\mu - ({P_{\pi^-}}^{\prime})_\mu][(P_e)^\mu + (P_p)^\mu - ({P_e}^{\prime})^\mu - ({P_{\pi^-}}^{\prime})^\mu][/math]
- In our case 4-vectors for particles are
[math](P_e)_\mu = ( 5.736, 0, 0, 5.736 GeV)[/math]
[math](P_p)_\mu = (m_p, 0, 0, 0)[/math]
[math]({P_e}^{\prime})_\mu = (4.4914861, -0.549, 0.974, 4.3501 )[/math]
[math]({P_{\pi^-}}^{\prime})_\mu = (0.575721, 0.1052, -0.4394, 0.3282)[/math]
- Plug and chug
[math]{M_x}^2 = [( 5.736, 0, 0, 5.736 GeV) + ( m_p, 0, 0, 0 ) - (4.4914861, -0.549, 0.974, 4.3501 ) - (0.575721, 0.1052, -0.4394, 0.3282)[/math]] [[math]\left (\begin{matrix} 5.736 \\ 0 \\ 0 \\ 5.736 \end{matrix} \right )[/math] + [math]\left (\begin{matrix} m_p \\ 0 \\ 0 \\ 0 \end{matrix} \right) [/math] - [math]\left (\begin{matrix} 4.4914861 \\ -0.549 \\ 0.974 \\ 4.3501 \end{matrix} \right) [/math] - [math]\left ( \begin{matrix}0.575721 \\ 0.1052 \\ -0.4394 \\ 0.3282 \end{matrix} \right) ] = 0.981198614 GeV^2[/math]
[math]M_x = 0.9905547 GeV[/math]
Example of the Missing Mass Calculation for the following reaction [math]\vec{e}p \rightarrow (e^-)^{\prime} n \pi^+[/math]
Used file dst27095_05.B00. Target [math]NH_3[/math], Beam Energy 5.735 GeV and Torus Current +2250. Event_number=3106861
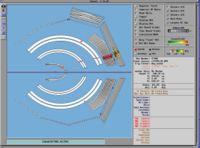
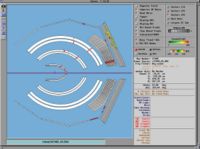
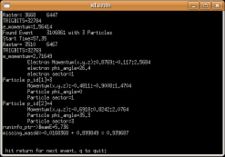
- [math]p_e = 5.736 Gev \sim E_e[/math] : electron mass is negligible
- [math]m_p = 0.938 GeV[/math] : Mass of a proton
- [math]m_n = 0.939566 GeV[/math] : Mass of a neutron
- [math]\beta_{cm} = \frac{5.736}{6.674} = 0.859 \lt 1[/math]
- [math]\gamma_{cm} = \frac{1}{\sqrt{1 - \beta_{cm}^2}} = \frac{1}{\sqrt{1 - 0.859^2}} = 1.9559[/math]
- [math]\left ( \begin{matrix} {E_e}^{\prime} \\ p_{ex}^{\prime} \\ p_{ey}^{\prime} \\ p_{ez}^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma_{cm} & 0 & 0 & -\gamma_{cm} \beta_{cm} \\ 0 & 1 &0 &0 \\ 0 &0 &1 &0 \\ -\gamma_{cm} \beta_{cm} &0 &0 &\gamma_{cm}\end{matrix} \right ] \left ( \begin{matrix} E_e=2.7165 \\ 0.8769 \\ -0.117 \\ 2.5684 \end{matrix} \right )[/math]
- [math]\left ( \begin{matrix} {E_n}^{\prime} \\ p_{nx}^{\prime} \\ p_{ny}^{\prime} \\ p_{nz}^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma_{cm} & 0 & 0 & -\gamma_{cm} \beta_{cm} \\ 0 & 1 &0 &0 \\ 0 &0 &1 &0 \\ -\gamma_{cm} \beta_{cm} &0 &0 & \gamma_{cm} \end{matrix} \right ] \left ( \begin{matrix} E_n =2.0218 \\ -0.4811 \\ -0.9008 \\ 1.4704 \end{matrix} \right )[/math]
- [math]\left ( \begin{matrix} {E_{\pi^+}}^{\prime} \\ p_{\pi^+ x}^{\prime} \\ p_{{\pi^+} y}^{\prime} \\ p_{{\pi^+} z}^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma_{cm} & 0 & 0 & -\gamma_{cm} \beta_{cm} \\ 0 & 1 &0 &0 \\ 0 &0 &1 &0 \\ -\gamma_{cm} \beta_{cm} &0 &0 & \gamma_{cm} \end{matrix} \right ] \left ( \begin{matrix} E_{\pi^+} =2.3431 \\ -0.6918 \\ 0.8242 \\ 2.0764 \end{matrix} \right )[/math]
- Electron
- [math]\left ( \begin{matrix} {E_e}^{\prime} \\ p_{ex}^{\prime} \\ p_{ey}^{\prime} \\ p_{ez}^{\prime} \end{matrix} \right )= \left ( \begin{matrix} 2.7165 \gamma_{cm} - 2.5684 \gamma_{cm} \beta_{cm} \\ 0.8769 \\ -0.117 \\ -2.7165\gamma_{cm} \beta_{cm} + 2.5684 \gamma_{cm} \end{matrix} \right ) = \left ( \begin{matrix} 0.99569 \\ 0.8769 \\ -0.117 \\ 0.45728 \end{matrix} \right )[/math]
- Neutron
- [math]\left ( \begin{matrix} {E_n}^{\prime} \\ p_{nx}^{\prime} \\ p_{ny}^{\prime} \\ p_{nz}^{\prime} \end{matrix} \right )= \left ( \begin{matrix} 2.0218\gamma_{cm} - 1.4704 \gamma_{cm} \beta_{cm} \\ -0.4811 \\ -0.9008 \\-2.0218 \gamma_{cm} \beta_{cm} + 1.4704\gamma_{cm} \end{matrix} \right ) = \left ( \begin{matrix} 1.4828 \\ -0.4811 \\ -0.9008 \\ -0.52256 \end{matrix} \right )[/math]
- [math]\pi^+[/math]
- [math]\left ( \begin{matrix} {E_{\pi^+}}^{\prime} \\ p_{\pi^+ x}^{\prime} \\ p_{{\pi^+} y}^{\prime} \\ p_{{\pi^+} z}^{\prime} \end{matrix} \right )= \left ( \begin{matrix} 2.3431\gamma_{cm} - 2.0764 \gamma_{cm} \beta_{cm} \\ -0.6918 \\ 0.8242 \\ -2.3431 \gamma_{cm} \beta_{cm} + 2.0764\gamma_{cm} \end{matrix} \right ) = \left ( \begin{matrix} 1.09257 \\ -0.6918 \\ 0.8242 \\ 0.1226 \end{matrix} \right )[/math]
[math]\vec {P_{tot}}^{\prime} = (p_{ex}^{\prime} + p_{nx}^{\prime} + p_{\pi^+x}^{\prime})\hat{x} + (p_{ey}^{\prime} + p_{ny}^{\prime} + p_{\pi^+y}^{\prime})\hat{y} + (p_{ez}^{\prime} + p_{nz}^{\prime} + p_{\pi^+z}^{\prime})\hat{z} = -0.296 \hat{x} + -0.1936 \hat{y} + 0.0573 \hat{z} [/math]
- Missing Mass Calculation
- Below is the conservation of the 4-momentum
[math](P_e)^\mu + (P_p)^\mu = ({P_e}^{\prime})^\mu + ({P_X}^{\prime})^\mu + ({P_{\pi^+}}^{\prime})^\mu[/math]
[math](P_e)_\mu + (P_p)_\mu = ({P_e}^{\prime})_\mu + ({P_X}^{\prime})_\mu + ({P_{\pi^+}}^{\prime})_\mu[/math]
- Solving it for the final neutron state
[math]{M_x}^2 = ({P_X}^{\prime})_\mu({P_X}^{\prime})^\mu = [(P_e)_\mu + (P_p)_\mu - ({P_e}^{\prime})_\mu - ({P_{\pi^+}}^{\prime})_\mu][(P_e)^\mu + (P_p)^\mu - ({P_e}^{\prime})^\mu - ({P_{\pi^+}}^{\prime})^\mu][/math]
- The 4-vectors for the particles in this event
[math](P_e)_\mu = ( 5.736, 0, 0, 5.736 GeV)[/math]
[math](P_p)_\mu = (m_p, 0, 0, 0)[/math]
[math]({P_e}^{\prime})_\mu = (2.7164, 0.8769, -0.117, 2.5684 )[/math]
[math]({P_{\pi^+}}^{\prime})_\mu = (2.3431, -0.6918, 0.8242, 2.0764)[/math]
[math]{M_x}^2 = [( 5.736, 0, 0, 5.736 GeV) + ( m_p, 0, 0, 0 ) - ( 2.7164, 0.8769, -0.117, 2.5684 ) - ( 2.3431, -0.6918, 0.8242, 2.0764 )[/math]] [[math]\left (\begin{matrix} 5.736 \\ 0 \\ 0 \\ 5.736 \end{matrix} \right )[/math] + [math]\left (\begin{matrix} m_p \\ 0 \\ 0 \\ 0 \end{matrix} \right) [/math] - [math]\left (\begin{matrix} 2.7164 \\ 0.8769 \\ -0.117 \\ 2.5684 \end{matrix} \right) [/math] - [math]\left ( \begin{matrix} 2.3431 \\ -0.6918 \\ 0.8242 \\ 2.0764\end{matrix} \right) ] = 0.882724889 GeV^2[/math]
[math]M_x = 0.9395344 GeV[/math]
[math]\phi_{diff}^{LAB} = \phi_e^{LAB} - \phi_{\pi^+}^{LAB} = (120 + 35.3) -26.4 = 128.9[/math]
Missing_Mass(experimental data)
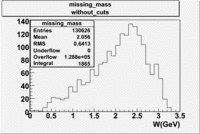
The mean value of the missing mass is around 2.056 GeV.
[math]\phi[/math] angle
[math]\phi[/math] angle for electrons and pions ([math]\pi^+[/math]) in lab frame [math]\phi_{e^-}^{LAB}[/math], [math]\phi_{\pi^+}^{LAB}[/math]
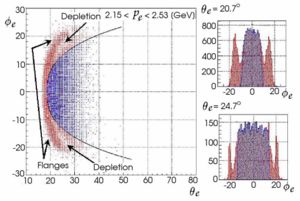 Electron fiducial cut at electron momentum range : 2.15 < [math]p_e[/math] < 2.53 GeV for sector 1. The histograms on the right show the < [math]\phi_e[/math] distributions at two values of [math]\theta_e[/math]. The highlighted area in the center indicates the selected fiducial range. [1] |
[2]
Phi angles
Below is shown histograms before changing angles by sectors for pions and electrons.
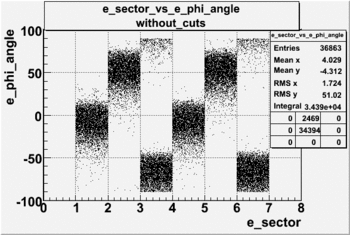
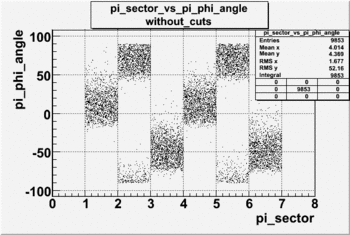
| [math]\phi[/math] ANGLE DISTRIBUTION FOR ELECTRONS AND PIONS(in each event we have just two particles eelctron and positive pion), FILE dst27095_05
|
| ELECTRONS |
PIONS(prt_id=4)
|
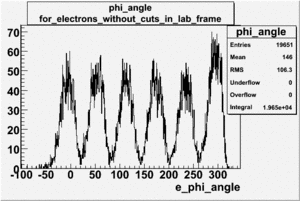
|
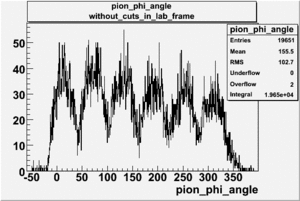
|
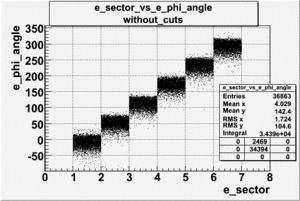
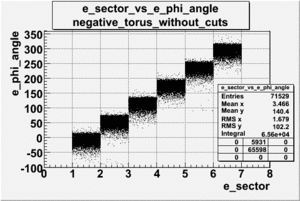
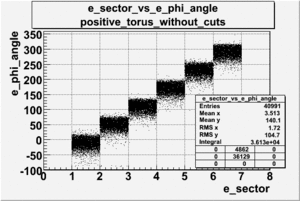
| SECTOR_VS_[math]\phi[/math] FOR ELECTRONS AND PIONS, FILE dst27095_05
|
| ELECTRONS |
PIONS(prt_id=4)
|
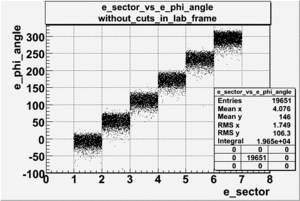
|
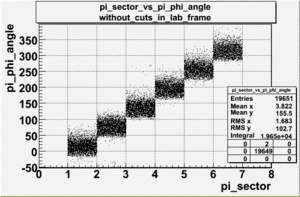
|
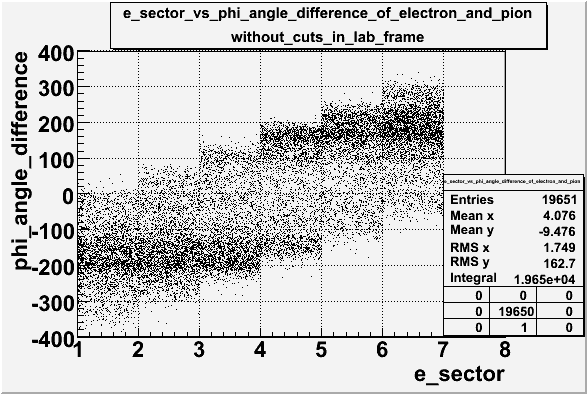
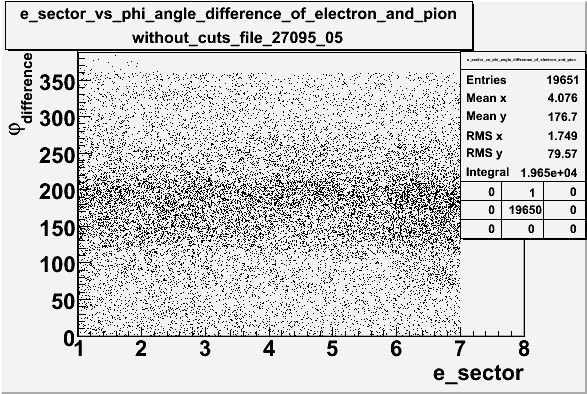
Graph [math]\phi_{\pi}^{CM}[/math] for Pions hitting paddle #7. The y-axis should be pion counting rate in units of pions per nanCoulomb.
[math]\phi[/math] angle in the Center of Mass Frame
The variables below are in Lab Frame:
From [math]\vec{e}p \rightarrow n \pi^+[/math] from CLAS
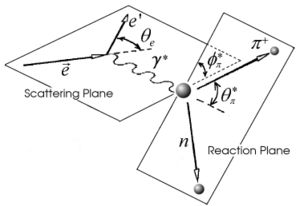 Kinematics of single [math]\pi^+[/math] electroproduction |
From the above picture we can write down the momentum x,y and z components for pion in terms of angle and total momentum.
[math]{p_{\pi x}}^{LAB} = p_{\pi}^{LAB} {sin {\theta}}_{\pi}^{LAB} cos {\phi}_{\pi}^{LAB}[/math]
[math]{p_{\pi y}}^{LAB} = p_{pi}^{LAB} {sin {\theta}}_{\pi}^{LAB} sin {\phi}_{\pi}^{LAB}[/math]
[math]{\phi}_{\pi}^{LAB} = arctg(\frac{{p_{\pi y}}^{LAB}}{{p_{\pi x}}^{LAB}})[/math]
where [math]{p_{\pi x}}^{LAB}[/math] and [math]{p_{\pi y}}^{LAB}[/math] are the x and y components of the pion momentum.
[math](P_e)^{\mu}[/math] - Initial electron 4-momentum
[math](P_N)^{\mu}[/math] - Target Nucleon 4-momentum
[math](P_e^{\prime})^{ \mu}[/math] - Scattered electron 4-momentum
[math](P_h)^{\mu}[/math] - Hadron final state 4-momentum
[math](P_m)^{\mu}[/math] - Meson final state 4-momentum
[math]h=n[/math], [math]m=\pi^+[/math] for [math]\vec{e} (\vec{p},\vec{e}^{\prime}) \pi^+ n[/math]
In Inclusive [math]\vec{e} (\vec{p},\vec{e}^{\prime}) X [/math]
Then The Missing Mass [math]W = (E_x ^2 - p_x ^2)[/math]
In Exclusive [math]\vec{e} (\vec{p},\vec{e}^{\prime}) \pi^+ X[/math]
Then Missing Mass [math] M = (E_h ^2 - p_h ^2)[/math]
Conservation of 4-momentum gives
[math](P_e)^\mu + (P_N)^\mu = ({P_e}^{\prime})^\mu + {P_h}^\mu + ({P_m})^\mu[/math]
[math]{P_h}^\mu = (P_e)^\mu - ({P_e}^{\prime})^\mu + (P_N)^\mu -({P_m})^\mu[/math]
[math]q^\mu[/math] - 4-momentum of the exchanged virtual photon([math]\gamma[/math])
[math]q^\mu = (P_e^{\prime})^\mu - P_e ^{\mu} = (E_e ^{\prime}, {\vec{p}_e} ^{\prime}) - (E_e, {\vec{p}_e}) = [/math]
[math] = (E_e ^{\prime} - E_e,{\vec{p}_e} ^{\prime} - {\vec{p}_e} ) = (0,{\vec{p}_e} ^{\prime} - {\vec{p}_e}) = (0, p_{e,x}^{\prime}\hat{x} + p_{e,y}^{\prime}\hat{y} + (p_{e,z}^{\prime} - p_{e,z})\hat{z})[/math]
[math]\phi_{\gamma} = tan^{-1}(\frac{p_{e y}^{\prime}}{p_{e x}^{\prime}})[/math]
[math]\theta_x = cos^{-1}(\frac{p_{e z}^{\prime} - p_{e z}}{\sqrt{{p_{e x}^{\prime}}^2 + {p_{e y}^{\prime}}^2 + ({p_{e z}^{\prime} - p_{e z}})^2}})[/math]
[math]p_{e x}^{\prime} = p_{e x}^{\prime CM}[/math]
[math]p_{e y}^{\prime} = p_{e y}^{\prime CM}[/math]
[math]p_{e z}^{\prime CM} = -E_e \gamma_{CM} \beta_{CM} + p_{e z }^{\prime LAB} \gamma_{CM}[/math]
[math]p_{e z}^{CM} = -p_{e z}^{LAB} \gamma_{CM} \beta_{CM} + p_{e z}^{LAB} \gamma_{CM}[/math]
[math]p_{e z}^{LAB} = Beam Energy [/math]
axis rotation
First the coordinate system is rotated around z-axis by [math]\phi_{\gamma}[/math] angle and then around y-axis by [math]\theta_x[/math] angle. Below is presented the transformation matrix.
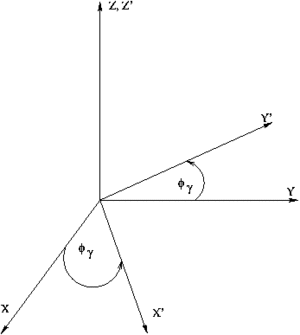
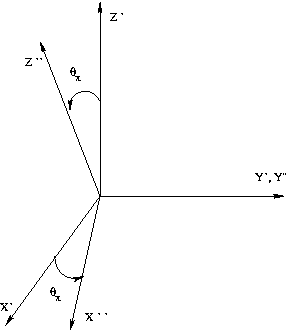
[math]\left ( \begin{matrix} p_{\pi x}^{LAB{\prime}} \\ p_{\pi y}^{LAB{\prime}} \\p_{\pi z}^{LAB{\prime}} \end{matrix} \right )= \left [ \begin{matrix} cos {\theta}_x & 0 & -sin {\theta_x} \\ 0 & 1 &0 \\ sin {\theta_x} &0 & cos {\theta_x} \end{matrix} \right ] \left [ \begin{matrix} cos {\phi_{\gamma}} & sin {\phi_{\gamma}} & 0 \\ -sin {\phi_{\gamma}} & cos {\phi_{\gamma}} &0 \\ 0 &0 & 1 \end{matrix} \right ] \left ( \begin{matrix} p_{\pi x}^{LAB} \\p_{\pi y}^{LAB} \\ p_{\pi z}^{LAB} \end{matrix} \right ) = [/math]
[math]= \left ( \begin{matrix} cos {\theta}_x (cos {\phi_{\gamma}} p_{\pi x}^{LAB} + sin {\phi_{\gamma}} p_{\pi y}^{LAB}) - sin {\theta}_x p_{\pi z}^{LAB} \\ -sin {\phi_{\gamma}} p_{\pi x}^{LAB} + cos {\phi_{\gamma}} p_{\pi y}^{LAB} \\ sin {\theta}_x (cos {\phi_{\gamma}} p_{\pi x}^{LAB} + sin {\phi_{\gamma}} p_{\pi y}^{LAB}) + cos {\theta}_x p_{\pi z}^{LAB} \end{matrix} \right ) [/math]
[math]{\phi}_{\pi}^{LAB{\prime}} = tan^{-1}(\frac{{p_{\pi y}}^{LAB{\prime}}}{{p_{\pi x}}^{LAB{\prime}}}) = tan^{-1}(\frac{-sin{\phi_{\gamma}} \times p_{\pi x}^{LAB} + cos{\phi_{\gamma}} \times p_{\pi y}^{LAB}}{cos {\theta}_x (cos {\phi_{\gamma}} p_{\pi x}^{LAB} + sin {\phi_{\gamma}} p_{\pi y}^{LAB}) - sin {\theta}_x p_{\pi z}^{LAB}})[/math]
[math]{\phi}_{\pi}^{CM} = tan^{-1}(\frac{{p_{\pi y}}^{CM}}{{p_{\pi x}}^{CM}}) = tan^{-1}(\frac{-sin{\phi_{\gamma}} \times p_{\pi x}^{CM} + cos{\phi_{\gamma}} \times p_{\pi y}^{CM}}{cos {\theta}_x (cos {\phi_{\gamma}} p_{\pi x}^{CM} + sin {\phi_{\gamma}} p_{\pi y}^{CM}) - sin {\theta}_x p_{\pi z}^{CM}})[/math]
[math]p_{\pi x}^{CM} = p_{\pi x}^{LAB}[/math]
[math]p_{\pi y}^{CM} = p_{\pi y}^{LAB}[/math]
[math]p_{\pi z}^{CM} = -E_{\pi} \gamma_{CM} \beta_{CM} + p_{\pi z}^{LAB} \gamma_{CM}[/math]
Phi rate
|
|
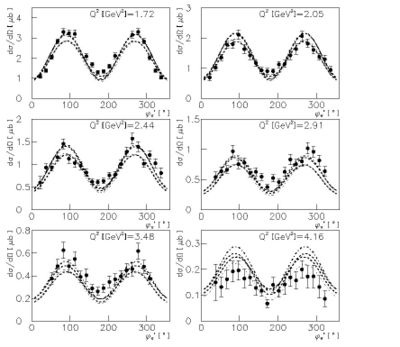 |[3]Differential cross section vs [math]{\phi_{\pi}}^*[/math] in the [math]\Delta(1232)[/math] region at fixed [math]cos \theta_{\pi}^* = -0.1[/math] for different bins in [math]Q^2[/math] |[3]Differential cross section vs [math]{\phi_{\pi}}^*[/math] in the [math]\Delta(1232)[/math] region at fixed [math]cos \theta_{\pi}^* = -0.1[/math] for different bins in [math]Q^2[/math]
|
phi angle in cm frame for different runs
start calculating cross -section
Luminosity Calculation for NH3(Ammonia) target
The target materials are located in the target cells. They are made out of polychlorotrifluoroethylene with a thickness of 0.2 mm. The cells itself are in diameter 15 (15.7) mm and in length 10 (12.7) mm, with 0.025 mm aluminum entrance windows and 0.05 mm kapton exit windows. [4]
Media:fill.factor.ps NH3 Filling Factor Evaluation, R. De Vita, July 1999
- [math]L = \frac{i_{scattered}}{\sigma} \sim i_{beam} \rho_{target} l_{target}[/math]
- [math]{\rho}_{ammonia} = 0.971 \frac{g}{cm^3}[/math][5]
- Avogadro Number: [math]N_A = 6.02214 \times\ 10^{23} {mol}^{-1} [/math]
- For file dst27095_05.B00 beam current is
- [math]i_{beam} = 6 nAmp [/math]
- [math]1 Amp = 6.242x10^{18}[/math] electrons per second
- [math]L = 6 nAmp \times 0.971 \frac{g}{cm^3} \times l_{target} \times cm =[/math]
- [math]= 6 \times 10^{-9} \times 6.242 \times 10^{18} \times 0.971 \times l_{target} \times \frac{ [\# of electrons]}{[second]} \times \frac{g}{cm^3} \times cm =[/math]
- [math]= 3.6366 \times 10^{10} \times l_{target} \times \frac{[ \# of electrons]}{[second]} \times \frac{g}{cm^2} =[/math]
- [math]= 3.6366 \times 10^{10} \times \frac{1 mol}{17} \times l_{target} \times \frac{[ \# of electrons]}{[second]} \times \frac{1}{cm^2} =[/math]
- [math]= 3.6366 \times 10^{10} \times \frac{6.02214 \times 10^{23}}{17} \times l_{target} \times \frac{[ \# of electrons]}{[second]} \times \frac{1}{cm^2} =[/math]
- [math]= 1.288 \times 10^{33} \times l_{target} \times \frac{[ \# of electrons]}{second \times cm^2}[/math]
- [math]= 1.288 \times 10^{33} \times 1 \times \frac{[ \# of electrons]}{second \times cm^2}[/math]
- [math]= 1.288 \times 10^{33} \frac{[ \# of electrons]}{second \times cm^2}[/math]
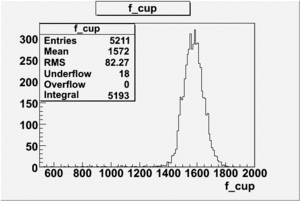
- [math]1 nAmp = 309[/math] counts on Faraday cup.[6]
- [math] L = 1.288 \times 10^{33} \frac{1572}{309 \times 6} \frac{[ \# of electrons]}{second \times cm^2} =[/math]
- [math]= 1.09209 \times 10^{33} \frac{[ \# of electrons]}{second \times cm^2}[/math]
- [math]= 1.09209 \times 30 \times 10^{33} \frac{[ \# of electrons]}{cm^2} = 3.3 \times 10^{34} \frac{[ \# of electrons]}{cm^2}[/math]
The luminosity of the continuous electron beam was [math]10^{34}[/math] [math]cm^{-2} sec^{-1}[/math] [7] [8]
- Cross Section Calculation
Media:cross_sections_1.pdf
- [math]\frac{d\sigma}{d\Omega} = \frac{1}{L} \frac{d^{2}N}{d\Omega dt}[/math]
where
- [math]L[/math] is the Luminosity.
- [math]N[/math] is the number of interactions.
- [math]\sigma[/math] is the total cross section.
- [math]d\Omega[/math] is the differential solid angle.
- [math] \frac{d\sigma}{d\Omega}[/math] is the differential cross section.
Pion Rates -vs- Paddle for opposite sign Torus fields
- using all events in which the first particle (the one which caused the trigger) is defined as an electrons and passes the
above electron cuts.
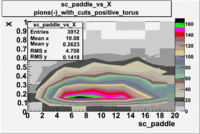
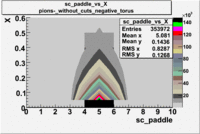
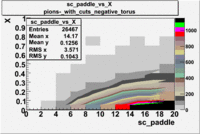
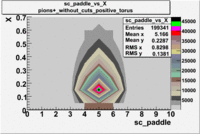
sc_paddle vs X_bjorken 5.7 GeV Beam Energy
| no cuts |
cuts |
no cuts |
cuts
|
| Electrons |
B > 0 |
|
B<0
|
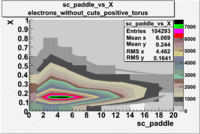
|
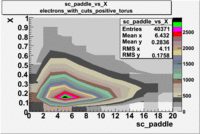
|
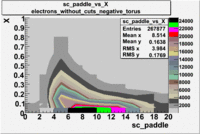
|
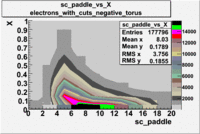
|
| [math]\pi^-[/math] |
B > 0 |
|
B<0
|
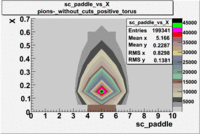
|
|
|
|
| [math]\pi^+[/math] |
B > 0 |
|
B<0
|
|
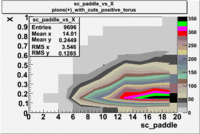
|
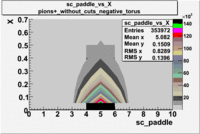
|
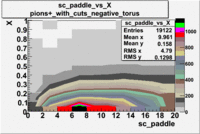
|
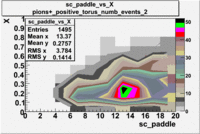
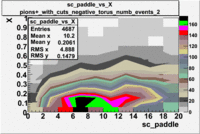
sc_paddle vs X_bjorken with cuts 5.7 GeV Beam Energy(number of events=2)
| [math]\pi^-[/math] |
[math]\pi^-[/math]
|
| B>0 |
B<0
|

|
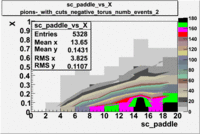
|
| [math]\pi^+[/math] |
[math]\pi^+[/math]
|
| B>0 |
B<0
|
|
|
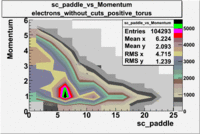
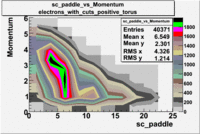
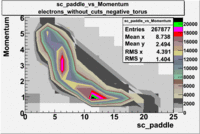
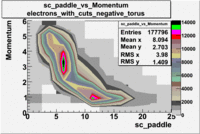
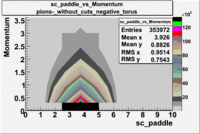
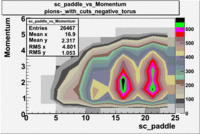
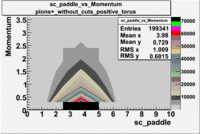
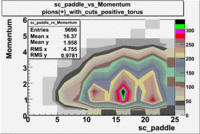
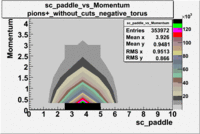
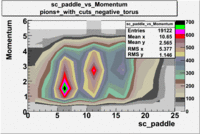
sc_paddle vs Momentum 5.7 GeV Beam Energy
There is a curvature problem. When B > 0 then I expect the high momentum electrons to hit the lower
paddle numbers (inbending). I can see this when I look at the B>0 plot for electrons with cuts.
When B < 0 then the electrons are bending outwards which makes me expect the the higher momentum
electrons will high the higher numbered paddles. I do not see this for B>0 with electron cuts.
| no cuts |
cuts |
no cuts |
cuts
|
| Electons |
B > 0 |
|
B<0
|
|
|
|
|
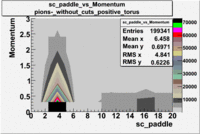
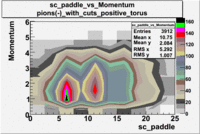
| [math]\pi^-[/math] |
B > 0 |
|
B<0
|
|
|
|
|
| [math]\pi^+[/math] |
B > 0 |
|
B<0
|
|
|
|
|
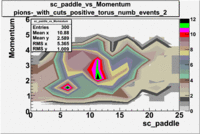
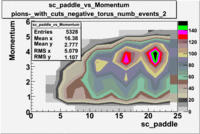
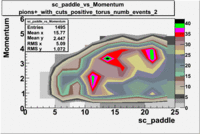
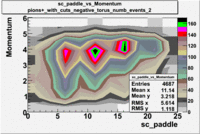
sc_paddle vs Momentum with cuts 5.7 GeV Beam Energy(number of events=2)
| [math]\pi^-[/math] |
[math]\pi^-[/math]
|
| B>0 |
B<0
|
|
|
| [math]\pi^+[/math] |
[math]\pi^+[/math]
|
| B>0 |
B<0
|
|
|
Used file dst26988_05.B00(Energy=5.7GeV and Torus=-2250)
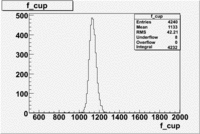
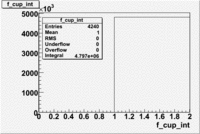
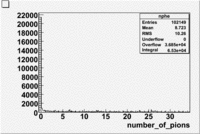
Paddle 7 Rates and statistics
The number of events per trigger is measured for the respective DST file above and then the Total number events in the data set is estimated from that.
| [math]X_{bj}[/math] |
[math]\pi^-[/math](B>0) |
|
[math]\pi^+[/math](B<0) |
|
|
Total Number Events [math](10^{3})[/math] |
Number events per [math]10^6[/math] triggers |
Total Number Events [math](10^{3})[/math] |
Number events per [math]10^6[/math] trigger
|
| 0.1 |
5.1 |
71 |
24.6 |
547
|
| 0.2 |
6.9 |
96 |
13.7 |
305
|
| 0.3 |
3.7 |
51 |
6.2 |
137
|
| 0.4 |
3.3 |
45 |
2.7 |
60
|
| 0.5 |
0.9 |
13 |
0.99 |
22
|
Paddle 17 Rates and statistics
| [math]X_{bj}[/math] |
[math]\pi^-[/math](B<0) |
|
[math]\pi^+[/math](B>0) |
|
|
Total Number Events [math](10^{3})[/math] |
Number events per [math]10^{6}[/math] trigger |
Total Number Events [math](10^{3})[/math] |
Number events per [math]10^{6}[/math] trigger
|
| 0.1 |
6.2 |
137 |
4.6 |
64
|
| 0.2 |
3.5 |
79 |
4.9 |
67
|
| 0.3 |
1.7 |
39 |
2.6 |
36
|
| 0.4 |
0.3 |
7 |
2.1 |
29
|
| 0.5 |
0.1 |
2 |
0.6 |
8
|
Paddle 5 and 8 Rates and statistics for electrons
| [math]X_{bj}[/math] |
[math]e^-[/math] sc_paddle=5 (B>0) |
|
[math]e^-[/math] sc_paddle=8 (B<0) |
|
|
Total Number Events [math](10^{3})[/math] |
Number events per [math]10^{6}[/math] trigger [math](10^{3})[/math] |
Total Number Events [math](10^{3})[/math] |
Number events per [math]10^{6}[/math] trigger [math](10^{4})[/math]
|
| 0.1 |
384.9 |
5.314 |
1665.2 |
3.706
|
| 0.2 |
382.5 |
5.282 |
977.8 |
2.176
|
| 0.3 |
264.9 |
3.657 |
567.1 |
1.262
|
| 0.4 |
159.5 |
2.202 |
328.6 |
0.7313
|
| 0.5 |
99 |
1.367 |
218.2 |
0.4856
|
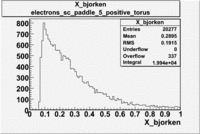
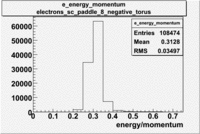
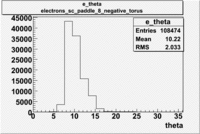
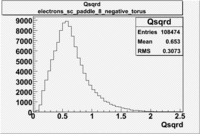
Histograms for 5.7 GeV Beam Energy
| Electron energy/momentum |
Electron Theta ([math]\theta[/math]) |
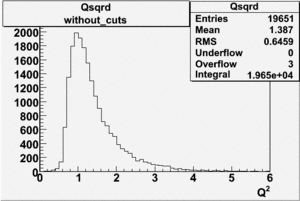
Electron Qsqrd |
Electron X_bjorken
|
| B>0 and sc_paddle=5 |
|
|
|
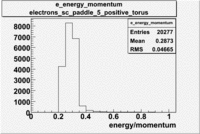
|
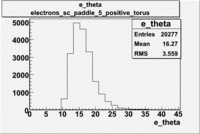
|
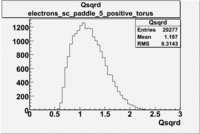
|
|
| B<0 and sc_paddle=8 |
|
|
|
|
|
|
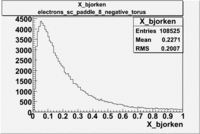
|
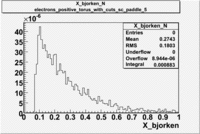
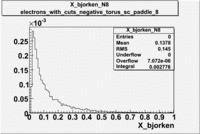
Normalized X_bjorken for electrons
| B>0 and sc_paddle=5 |
B<0 and sc_paddle=8
|
|
|
Asymmetries
Systematic Errors
Media:SebastianSysErrIncl.pdf Sebastian's Writeup
[Back to Analysis]







 |[3]Differential cross section vs in the region at fixed for different bins in
|[3]Differential cross section vs in the region at fixed for different bins in