Difference between revisions of "Comparing With Whitney Rates"
Jump to navigation
Jump to search



| (7 intermediate revisions by the same user not shown) | |||
| Line 13: | Line 13: | ||
For a 5cm target of LH2: | For a 5cm target of LH2: | ||
| − | <center><math>\rho_{target}\times l_{target}=\frac{70.85 kg}{1 m^3}\times \frac{1 mole}{2.02 g} \times \frac{1000g}{1 kg} \times \frac{6.022\times10^{23} molecules\ LH_2}{1 mole} \frac{2 atoms}{1\ molecule\ LH_2} \times \frac{1m^3}{(100 cm)^3} \times \frac{5 cm}{ }=\frac{2.11\times 10^{23}}{cm^2} \times \frac{ | + | <center><math>\rho_{target}\times l_{target}=\frac{70.85 kg}{1 m^3}\times \frac{1 mole}{2.02 g} \times \frac{1000g}{1 kg} \times \frac{6.022\times10^{23} molecules\ LH_2}{1 mole} \frac{2 atoms}{1\ molecule\ LH_2} \times \frac{1m^3}{(100 cm)^3} \times \frac{5 cm}{ }=\frac{2.11\times 10^{23}}{cm^2} \times \frac{1^{-24} cm^{2}}{barn}=0.211 barns^{-1}</math></center> |
| Line 112: | Line 112: | ||
<center><math>N_{Moller} =R_{Moller}\cdot t_{simulated}=\frac{9.97\times 10^{9}Moller}{s} \cdot 9.54\times 10^{-5} s=951138\ Moller</math></center> | <center><math>N_{Moller} =R_{Moller}\cdot t_{simulated}=\frac{9.97\times 10^{9}Moller}{s} \cdot 9.54\times 10^{-5} s=951138\ Moller</math></center> | ||
| + | Using just the scattered particles, for the total time run, | ||
| + | <center><math>\sigma=\frac{ N_{scattered}}{ N_{incident}}\frac{1}{\rho \ell}\Rightarrow N_{incident}=\frac{ N_{scattered}}{\sigma \rho \ell}=\frac{ 1000000}{ .078\cdot 2.11\times 10^{-1}}\approx 6\times 10^7\ incident</math></center> | ||
| − | <center><math>\sigma=\frac{N_{ | + | |
| + | If we view the window for each region as how many events can be detected per second | ||
| + | |||
| + | <center><math>\sigma=\frac{ t\ N_{scattered}}{\Delta t N_{incident}}\frac{1}{\rho \ell}\Rightarrow N_{incident}=\frac{t\ N_{scattered}}{\Delta t\sigma \rho \ell}=\frac{0.0954\times 10^{-3}\ s\ \times 1000000}{250 \times 10^{-9}\ s \times .078\cdot 2.11\times 10^{-1}}\approx 6\times 10^7\ incident \times 380 \approx 2\times 10^{10}</math></center> | ||
<center><math>\left ( \frac{Number\ of\ hits}{Moller\ electron}\right ) \left (\frac{Moller\ electrons}{incidents\ electron} \right) \left (\frac{incident\ electrons}{sec} \right )</math></center> | <center><math>\left ( \frac{Number\ of\ hits}{Moller\ electron}\right ) \left (\frac{Moller\ electrons}{incidents\ electron} \right) \left (\frac{incident\ electrons}{sec} \right )</math></center> | ||
Latest revision as of 20:32, 28 March 2018
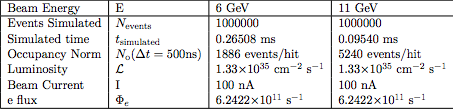
Using the values from Whitney:

For a 5cm target of LH2:
Using the beam current of 100nA,
Given the beam Luminosity of:
We can check to make sure the density makes sense
Using the values from Whitney :
https://wiki.iac.isu.edu/index.php/CLAS12_RateEst_byWA
| Energy | 6 GeV | 11 GeV |
| Process | (nb) | (nb) |
| Moller | 22773001 | 75008636 |
| DIS + radiative tail | 128 | 83 |
| Elastic e-p | 5511220 | 3670740 |
| Elastic radiative tail | 24705 | 12944 |
| π0 electro-production | 14802 | 17908 |
| π0 photo-production | 569 | 852 |
| π+ electro-production | 4032 | 5536 |
| π+ photo-production | 282 | 487 |
| π− electro-production | 2806 | 3843 |
| π− photo-production | 199 | 342 |
| Total | 2.83317E7 | 7.87214E7 |



Similarly,
Using just the scattered particles, for the total time run,
If we view the window for each region as how many events can be detected per second