Difference between revisions of "T-Channel"
Jump to navigation
Jump to search
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <center><math>\ | + | <center><math>\underline{\textbf{Navigation}}</math> |
[[S-Channel|<math>\vartriangleleft </math>]] | [[S-Channel|<math>\vartriangleleft </math>]] | ||
| Line 11: | Line 11: | ||
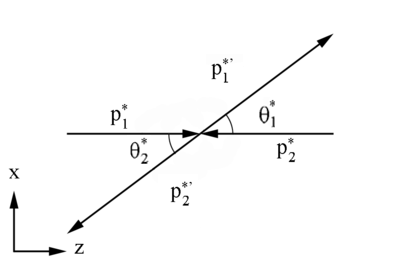
The t quantity is known as the square of the 4-momentum transfer | The t quantity is known as the square of the 4-momentum transfer | ||
| − | <center><math>t \equiv \left({\mathbf P_1^*}- {\mathbf P_1^{'*}}\right)^2=\left({\mathbf P_2^{*}} | + | <center><math>t \equiv \left({\mathbf P_1^*}- {\mathbf P_1^{'*}}\right)^2=\left({\mathbf P_2^{*}}- {\mathbf P_2^{'*}}\right)^2</math></center> |
<center>[[File:400px-CMcopy.png]]</center> | <center>[[File:400px-CMcopy.png]]</center> | ||
| Line 20: | Line 20: | ||
| − | <center><math>t \equiv P_1^{*2}- | + | <center><math>t \equiv \mathbf P_1^{*2}-2 \mathbf P_1^* \mathbf P_1^{'*}+ \mathbf P_1^{'*2}</math></center> |
| − | <center><math>t \equiv 2m_1^2-2E_1^*E_1^{'*}+ | + | <center><math>t \equiv 2m_1^2-2E_1^*E_1^{'*}+2 \vec p \ _1^* \vec p \ _1^{'*}</math></center> |
| − | |||
| + | In the center of mass frame of reference, | ||
| − | <center><math>t \equiv - | + | <center><math> E^* \equiv E_1^*=E_1^{'*} = E_2^*=E_2^{'*} = E_1^*=E_2^*</math></center> |
| + | |||
| + | |||
| + | and | ||
| + | |||
| + | |||
| + | <center><math>|p^*| \equiv | \vec p \ _1^*|=| \vec p \ _1^{'*}| =| \vec p \ _2^*|=| \vec p \ _2^{'*}|</math></center> | ||
| + | |||
| + | |||
| + | and <math>\theta_1</math> is the angle between <math>\vec p \ _1^* </math> and <math> \vec p \ _1^{'*}</math> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>t \equiv 2m_1^*-2E_1^{*2}+2 |p |^{*2}cos\ \theta</math></center> | ||
| + | |||
| + | |||
| + | Using the relativistic term for Energy | ||
| + | |||
| + | |||
| + | <center><math>E^2=\vec p \ ^2+m^2</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>t \equiv -2 p \ ^{*2}(1-cos\ \theta)</math></center> | ||
| Line 35: | Line 58: | ||
| − | <center><math>\ | + | <center><math>\underline{\textbf{Navigation}}</math> |
[[S-Channel|<math>\vartriangleleft </math>]] | [[S-Channel|<math>\vartriangleleft </math>]] | ||