Difference between revisions of "Theta Dependent Components"
Jump to navigation
Jump to search
(Created page with "<center> 400 px</center> <center>'''Figure 3: Definition of Moller electron variables in the CM Frame in the x-z plane.'''</center> <center>Using <math>\the…") |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <center><math>\textbf{\underline{Navigation}}</math> | ||
| + | |||
| + | [[Determining_Momentum_Components_After_Collision_in_CM_Frame|<math>\vartriangleleft </math>]] | ||
| + | [[VanWasshenova_Thesis#Weighted_Isotropic_Distribution_in_Lab_Frame|<math>\triangle </math>]] | ||
| + | [[Phi_Dependent_Components|<math>\vartriangleright </math>]] | ||
| + | |||
| + | </center> | ||
| + | |||
| + | |||
| + | |||
| + | =4.1.3.1 Theta Dependent Components= | ||
| + | |||
<center>[[File:xz_lab.png | 400 px]]</center> | <center>[[File:xz_lab.png | 400 px]]</center> | ||
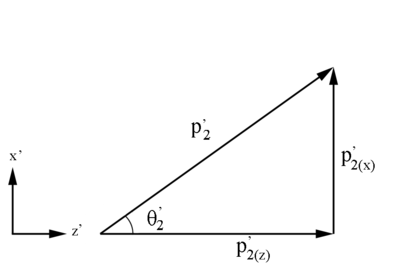
<center>'''Figure 3: Definition of Moller electron variables in the CM Frame in the x-z plane.'''</center> | <center>'''Figure 3: Definition of Moller electron variables in the CM Frame in the x-z plane.'''</center> | ||
| Line 23: | Line 35: | ||
<center><math>\Longrightarrow p^'_{2(z)}\ should\ always\ be\ negative</math></center> | <center><math>\Longrightarrow p^'_{2(z)}\ should\ always\ be\ negative</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\textbf{\underline{Navigation}}</math> | ||
| + | |||
| + | [[Determining_Momentum_Components_After_Collision_in_CM_Frame|<math>\vartriangleleft </math>]] | ||
| + | [[VanWasshenova_Thesis#Weighted_Isotropic_Distribution_in_Lab_Frame|<math>\triangle </math>]] | ||
| + | [[Phi_Dependent_Components|<math>\vartriangleright </math>]] | ||
| + | |||
| + | </center> | ||