Difference between revisions of "DC Super Layer 1:Layer 1"
| (17 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <center><math>\ | + | <center><math>\underline{\textbf{Navigation}}</math> |
[[CED_Verification_of_DC_Angle_Theta_and_Wire_Correspondance|<math>\vartriangleleft </math>]] | [[CED_Verification_of_DC_Angle_Theta_and_Wire_Correspondance|<math>\vartriangleleft </math>]] | ||
| − | [[ | + | [[VanWasshenova_Thesis#Determining_wire-theta_correspondence|<math>\triangle </math>]] |
[[DC_Binning_Based_On_Wire_Numbers|<math>\vartriangleright </math>]] | [[DC_Binning_Based_On_Wire_Numbers|<math>\vartriangleright </math>]] | ||
| Line 56: | Line 56: | ||
| − | <center><math>\arctan{\frac{22.2092+1.212}{242.5779-0.5652}}=\arctan{\frac{23.4212}{242.0127}}=\arctan{0.0967}=5.53^{\circ}</math></center> | + | <center><math>\arctan{\frac{22.2092+1.212}{242.5779-0.5652}}=\arctan{\frac{23.4212}{242.0127}}=\arctan{0.0967}=5.53^{\circ}=\tan{\theta_2}</math></center> |
| Line 62: | Line 62: | ||
| − | <center><math>\tan{\ | + | <center><math>\tan{\theta_n}=\frac{x-\Delta x+n\Delta x}{z-\Delta z+n\Delta z}\Rightarrow \theta_n=\arctan{\frac{x+n\Delta x}{z+n\Delta z}}</math></center> |
where | where | ||
<center><math>x_0=22.2092-1.212\approx 20.9972cm</math></center> | <center><math>x_0=22.2092-1.212\approx 20.9972cm</math></center> | ||
| + | |||
<center><math>z_0=242.5779+0.5652\approx 243.1431cm</math></center> | <center><math>z_0=242.5779+0.5652\approx 243.1431cm</math></center> | ||
| − | <center><math>\ | + | <center><math>\theta_n=\arctan{\frac{20.9972+n1.212}{243.1431-n0.5652}}</math></center> |
| − | <center><math>\tan{\ | + | <center><math>\tan{\theta_n}=\frac{20.9972+n1.212}{243.1431-n0.5652}\Rightarrow \tan{ \theta_n}=-2.14437 + \frac{959.637}{430.189 - n}\Rightarrow 430.189 - n = \frac{959.637}{\tan{ \theta_n}+2.14437}</math></center> |
| − | <center><math>\Rightarrow n = \frac{-959.637}{\tan{ \ | + | <center><math>\Rightarrow n = \frac{-959.637}{\tan{ \theta_n}+2.14437}+430.189</math></center> |
Using Mathematica, a series expansion about n=0 can be found: | Using Mathematica, a series expansion about n=0 can be found: | ||
<pre> | <pre> | ||
| − | In[ | + | In[2]:= Series[ArcTan[(20.9972+1.212 n)/(243.1431-0.5652 n)],{n,0,4}] |
| − | Out[ | + | Out[2]= 0.0861437+0.00514708 n+9.67686*10^-6 n^2-2.72596*10^-8 n^3-2.22159*10^-10 n^4+O[n]^5 |
</pre> | </pre> | ||
| − | <center><math>\theta\approx 0. | + | <center><math>\theta\approx 0.0861437+0.00514708 n+9.67686 \times10^{-6} n^2-2.72596 \times 10^{-8} n^3</math></center> |
| Line 93: | Line 94: | ||
<pre> | <pre> | ||
| − | In[ | + | In[3]:= 180(0.08614365821719583`+0.005147076698801422` n+9.676859262994711`*^-6 n^2-2.7259639443492433`*^-8 n^3-2.2215881081233252`*^-10 n^4+O[n]^5)/3.14159265359 |
| − | Out[ | + | Out[3]= 4.93567+0.294906 n+0.000554443 n^2-1.56186*10^-6 n^3-1.27288*10^-8 n^4+O[n]^5 |
</pre> | </pre> | ||
| − | <center><math>\theta\approx 4. | + | <center><math>\theta\approx 4.93567+0.294906 n+0.000554443 n^2-1.56186*10^{-6} n^3</math></center> |
| + | |||
| + | |||
| + | This tells us that the expression for theta will follow a function that comes from a series expansion. Using Mathematica, a line can be fitted to the data collected on the wire number to angle theta correspondence. | ||
| − | |||
| + | {| border=1 align=center | ||
| + | |+ Table 4: Calculated Superlayer 1 Wire-Angle Theta Correspondence in Degrees | ||
| + | |- style="font-weight:bold; text-align:center;" | ||
| + | ! style=" border:1px solid gray;"|Wire Number | ||
| + | ! style=" border:1px solid gray;"|Layer 1 | ||
| − | + | |- | |
| + | | style="border:1px solid gray;"|'''1''' | ||
| + | | style="border:1px solid gray;"|5.23 | ||
| + | |- | ||
| + | | style="border:1px solid gray;"|''' 2''' | ||
| + | | style="border:1px solid gray;"|5.53 | ||
| + | |- | ||
| + | | style="border:1px solid gray;"|'''77''' | ||
| + | | style="border:1px solid gray;"|29.80 | ||
| + | |- | ||
| + | | style="border:1px solid gray;"|'''78''' | ||
| + | | style="border:1px solid gray;"|30.13 | ||
| + | |- | ||
| + | | style="border:1px solid gray;"|'''79''' | ||
| + | | style="border:1px solid gray;"|30.46 | ||
| + | |- | ||
| + | | style="border:1px solid gray;"|'''110''' | ||
| + | | style="border:1px solid gray;"|40.45 | ||
| + | |- | ||
| + | | style="border:1px solid gray;"|'''111''' | ||
| + | | style="border:1px solid gray;"|40.76 | ||
| + | |- | ||
| + | | style="border:1px solid gray;"|''' 112''' | ||
| + | | style="border:1px solid gray;"|41.07 | ||
| + | |} | ||
Declaring the data set: | Declaring the data set: | ||
<pre> | <pre> | ||
| − | In[ | + | In[4]:= data1={{1,5.23},{2,5.53},{77,29.80},{78,30.13},{79,30.46},{110,40.45},{111,40.76},{112,41.07}} |
| − | Out[ | + | Out[4]= {{1,5.23},{2,5.53},{77,29.8},{78,30.13},{79,30.46},{110,40.45},{111,40.76},{112,41.07}} |
</pre> | </pre> | ||
| Line 119: | Line 151: | ||
Testing for a linear fit: | Testing for a linear fit: | ||
<pre> | <pre> | ||
| − | In[ | + | In[5]:= line1=Fit[data1,{1,n},n] |
| − | Out[ | + | Out[5]= 4.90443 +0.323148 n |
</pre> | </pre> | ||
| − | + | Examining the range limits for the angle theta for layer 1: | |
| Line 130: | Line 162: | ||
Taking the difference of the upper and lower limits in theta, | Taking the difference of the upper and lower limits in theta, | ||
| − | <center><math>\Delta degrees= | + | |
| + | <center><math>\theta=\arctan{\frac{20.9972+n1.212}{243.1431-n0.5652}}</math></center> | ||
| + | |||
| + | |||
| + | <center><math>\theta_{n=1}=\arctan{\frac{20.9972+(1)1.212}{243.1431-(1)0.5652}}=5.23\ \ \ \ \ \ \theta_{n=112}=\arctan{\frac{20.9972+(112)1.212}{243.1431-(112)0.5652}}=41.07</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <center><math>\Delta degrees=41.07^{\circ}-5.23^{\circ}=35.84^{\circ}</math></center> | ||
Dividing by the change in wire numbers (112-1=111), we find | Dividing by the change in wire numbers (112-1=111), we find | ||
| − | <center><math>\frac{\Delta degrees}{\Delta wire\ number}=\frac{ | + | <center><math>\frac{\Delta degrees}{\Delta wire\ number}=\frac{35.84^{\circ}}{111\ wires}\approx\ \frac{0.323^{\circ}}{wire\ number}</math></center> |
| − | This would imply that if the wires were evenly placed, their change in angle theta would increase by the factor of . | + | This would imply that if the wires were evenly placed, their change in angle theta would increase by the factor of .323 degrees for each increase in wire number, starting obviously with wire 1 at 5.23 degrees. In addition, this implies that the bin spacing for each wire would be around .323 degrees in width. |
| − | + | Checking this, we can find the difference between wires 1 and 2, | |
| − | <center><math>\frac{\Delta degree}{\Delta wire\ number}=\frac{5. | + | <center><math>\frac{\Delta degree}{\Delta wire\ number}=\frac{5.5277^{\circ}-5.2311^{\circ} }{wire\ number}=\frac{.2965^{\circ}}{wire\ number} </math></center> |
Similarly, finding the difference between wires 111 and 112, | Similarly, finding the difference between wires 111 and 112, | ||
| − | <center><math>\frac{\Delta degree}{\Delta wire\ number}=\frac{ | + | <center><math>\frac{\Delta degree}{\Delta wire\ number}=\frac{41.0740^{\circ}-40.7649^{\circ}}{wire\ number}=\frac{.0.3091^{\circ}}{wire\ number}</math></center> |
| + | |||
| + | |||
| + | These differing values show that the bin width is not uniform in length, therefore a first order, linear fit, will not suffice. The change in bin size, with respect to the angle theta covered, is due to the tilt of the wire plane. | ||
| + | |||
| + | |||
| + | |||
| + | |||
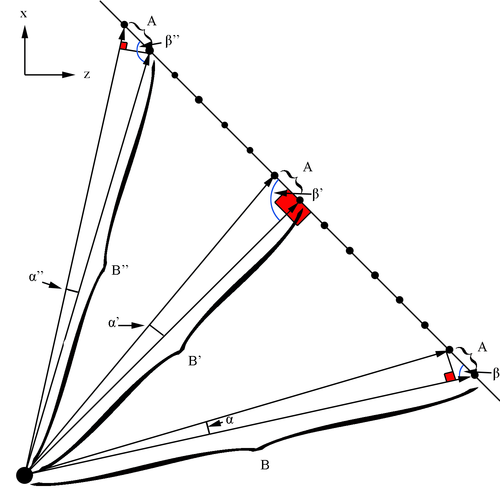
| + | [[File:Bin_angle_size.png|thumb|center|500px|alt=Geometry of Wire Bins Angular Size in DC|'''Figure 5.1.1:''' For a tilted plane, that is offset from the origin, the change in angle between uniformly spaced points depends on the tilt with respect to the beam line. The uniform distance between points, A, can be used to show the angle, <math>\alpha</math> each wire bin covers can be found using the law of sines. The interior angle <math>\beta</math>]] | ||
| + | |||
| + | Using the law of sines, | ||
| + | <center><math>\frac{\sin{\alpha}}{A}=\frac{\sin{\beta}}{B}</math></center> | ||
| − | |||
| + | <center><math>\Rightarrow \alpha=\arcsin{\frac{A \sin{\beta}}{B}}</math></center> | ||
| + | The range of <math>\beta</math> runs from near to 65 to almost 180 degrees. At <math>\theta=25^{\circ}</math> with respect to the positive z direction, a right triangle is created. Since the sine function is periodic and reaches its maximum at 90 degrees, this implies that the opposite side to this angle reaches its minimum. On either side of the right angle, as the angle <math>\beta</math> either increases or decreases, the function <math>\sin{\beta} will be smaller. This implies for movement in angle <math>\alpha</math> in a counter-clockwise direction, the angle <math>\beta</math> will continue to increase, while the length of B will decrease, then increase, reaching it's minimum at <math>\theta=25^{\circ}</math>. This also implies that <math>\alpha</math> will increase in size, then decrease, hitting its maximum at the same spot where <math>\beta</math> is at a minimum. | ||
Testing for a quadratic fit: | Testing for a quadratic fit: | ||
<pre> | <pre> | ||
| − | In[ | + | In[6]:= quad1=Fit[data1,{1,n,n^2},n] |
| − | Out[ | + | Out[6]= 4.89326 +0.324556 n-0.0000129154 n^2 |
</pre> | </pre> | ||
The quadratic fit does not work since it's first derivative | The quadratic fit does not work since it's first derivative | ||
| − | <center><math>\theta'\approx \Delta \theta=. | + | <center><math>\theta'\approx \Delta \theta=0.324556 -0.0000258\ n</math></center> |
| − | does not give the same spacing between low and high values of n as seen in the | + | does not give the same spacing between low and high values of n as seen in the calculated data. The coefficient near the zeroth order for the derivative will have to be smaller than .31 to find a correlation that would agree with calculated values. |
Testing for a polynomial of degree 3 fit: | Testing for a polynomial of degree 3 fit: | ||
<pre> | <pre> | ||
| − | In[ | + | In[7]:= polynomial1=Fit[data1,{1,n,n^2,n^3},n] |
| − | Out[ | + | Out[7]= 4.93253 +0.297371 n+0.000566298 n^2-3.04016*10^-6 n^3 |
</pre> | </pre> | ||
| − | This fit best matches the data found in | + | This fit best matches the data found in the calculated data |
| − | <center><math>\theta\equiv 4. | + | <center><math>\theta\equiv 4.93253 +0.297371 n+0.000566298 n^2-3.04016 \times 10^{-6} n^3</math></center> |
As discussed earlier, taking the 1st derivative of this function will give us the spacing of the bins as a function of wire number. | As discussed earlier, taking the 1st derivative of this function will give us the spacing of the bins as a function of wire number. | ||
| − | <center><math>\theta '\equiv 0. | + | <center><math>\theta '\equiv 0.297371 + 0.0011326 n - 9.12048 \times 10^{-6} n^2</math></center> |
The derivative of this function then will tell us where the bin spacing is at a minimum and a maximum. | The derivative of this function then will tell us where the bin spacing is at a minimum and a maximum. | ||
| − | <center><math>\theta ''\equiv . | + | <center><math>\theta ''\equiv 0.0011326 - 0.000018241 n</math></center> |
| + | |||
| + | <center><math>0.0011326 - 0.000018241 n=0\Rightarrow Bin\ Spacing\ Maximum\ at\ n=62.0909</math></center> | ||
| − | |||
| − | + | This is near the point of the plane where <math>\theta=25^{\circ}</math> as seen in the figure above. | |
| Line 201: | Line 255: | ||
| − | <center><math>\ | + | <center><math>\underline{\textbf{Navigation}}</math> |
[[CED_Verification_of_DC_Angle_Theta_and_Wire_Correspondance|<math>\vartriangleleft </math>]] | [[CED_Verification_of_DC_Angle_Theta_and_Wire_Correspondance|<math>\vartriangleleft </math>]] | ||
Latest revision as of 20:14, 15 May 2018
DC Super Layer 1:Layer 1
From the ced simulations
| Coordinates(cm) | Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 5 | Layer 6 |
|---|---|---|---|---|---|---|
| 1.22 | 1.22 | 1.22 | 1.22 | 1.21 | 1.22 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| .55 | .56 | .57 | .57 | .57 | .57 |
While the wire placement is off, the difference in x and z position is matched by the calculated values. Using the geometric construction for determining angle theta to wire 2:
This equation can be solved for a hypothetical wire 0, which will allow the wire number to be the multiplicative factor for the change from the starting position.
where
Using Mathematica, a series expansion about n=0 can be found:
In[2]:= Series[ArcTan[(20.9972+1.212 n)/(243.1431-0.5652 n)],{n,0,4}]
Out[2]= 0.0861437+0.00514708 n+9.67686*10^-6 n^2-2.72596*10^-8 n^3-2.22159*10^-10 n^4+O[n]^5
This expression will find the angle theta in radians given the wire number. To convert from radians to degrees, we can multiply by 180 and divide by Pi.
In[3]:= 180(0.08614365821719583`+0.005147076698801422` n+9.676859262994711`*^-6 n^2-2.7259639443492433`*^-8 n^3-2.2215881081233252`*^-10 n^4+O[n]^5)/3.14159265359 Out[3]= 4.93567+0.294906 n+0.000554443 n^2-1.56186*10^-6 n^3-1.27288*10^-8 n^4+O[n]^5
This tells us that the expression for theta will follow a function that comes from a series expansion. Using Mathematica, a line can be fitted to the data collected on the wire number to angle theta correspondence.
| Wire Number | Layer 1 |
|---|---|
| 1 | 5.23 |
| 2 | 5.53 |
| 77 | 29.80 |
| 78 | 30.13 |
| 79 | 30.46 |
| 110 | 40.45 |
| 111 | 40.76 |
| 112 | 41.07 |
Declaring the data set:
In[4]:= data1={{1,5.23},{2,5.53},{77,29.80},{78,30.13},{79,30.46},{110,40.45},{111,40.76},{112,41.07}}
Out[4]= {{1,5.23},{2,5.53},{77,29.8},{78,30.13},{79,30.46},{110,40.45},{111,40.76},{112,41.07}}
Testing for a linear fit:
In[5]:= line1=Fit[data1,{1,n},n]
Out[5]= 4.90443 +0.323148 n
Examining the range limits for the angle theta for layer 1:
Taking the difference of the upper and lower limits in theta,
Dividing by the change in wire numbers (112-1=111), we find
This would imply that if the wires were evenly placed, their change in angle theta would increase by the factor of .323 degrees for each increase in wire number, starting obviously with wire 1 at 5.23 degrees. In addition, this implies that the bin spacing for each wire would be around .323 degrees in width.
Checking this, we can find the difference between wires 1 and 2,
Similarly, finding the difference between wires 111 and 112,
These differing values show that the bin width is not uniform in length, therefore a first order, linear fit, will not suffice. The change in bin size, with respect to the angle theta covered, is due to the tilt of the wire plane.
Using the law of sines,
The range of runs from near to 65 to almost 180 degrees. At with respect to the positive z direction, a right triangle is created. Since the sine function is periodic and reaches its maximum at 90 degrees, this implies that the opposite side to this angle reaches its minimum. On either side of the right angle, as the angle either increases or decreases, the function in a counter-clockwise direction, the angle will continue to increase, while the length of B will decrease, then increase, reaching it's minimum at . This also implies that will increase in size, then decrease, hitting its maximum at the same spot where is at a minimum.
Testing for a quadratic fit:
In[6]:= quad1=Fit[data1,{1,n,n^2},n]
Out[6]= 4.89326 +0.324556 n-0.0000129154 n^2
The quadratic fit does not work since it's first derivative
does not give the same spacing between low and high values of n as seen in the calculated data. The coefficient near the zeroth order for the derivative will have to be smaller than .31 to find a correlation that would agree with calculated values.
Testing for a polynomial of degree 3 fit:
In[7]:= polynomial1=Fit[data1,{1,n,n^2,n^3},n]
Out[7]= 4.93253 +0.297371 n+0.000566298 n^2-3.04016*10^-6 n^3
This fit best matches the data found in the calculated data
As discussed earlier, taking the 1st derivative of this function will give us the spacing of the bins as a function of wire number.
The derivative of this function then will tell us where the bin spacing is at a minimum and a maximum.
This is near the point of the plane where as seen in the figure above.