Difference between revisions of "ISU Coloq 11-3-2014"
(→CPAA) |
|||
| (9 intermediate revisions by the same user not shown) | |||
| Line 130: | Line 130: | ||
[[File:CLAS_InelasticSpectrum_2012.png | 200 px]] | [[File:CLAS_InelasticSpectrum_2012.png | 200 px]] | ||
| + | |||
| + | Get picture from Figure 1.3 on pg 13 to show how cross section changes with Q^2 | ||
| + | |||
| + | http://arxiv.org/pdf/0812.2144.pdf | ||
| + | |||
| + | |||
| + | F1 for several Q^2 to show how it smooths out | ||
| + | |||
| + | http://www.jlab.org/Hall-B/secure/eg1/Models/InclusiveModels.html | ||
| + | |||
| + | DIS scattering theory | ||
| + | |||
| + | |||
| + | http://www.physics.umd.edu/courses/Phys741/xji/chapter4.pdf | ||
===The Delta Resonance=== | ===The Delta Resonance=== | ||
| Line 272: | Line 286: | ||
[[File:TDC7023_1.png | 400 px]] | [[File:TDC7023_1.png | 400 px]] | ||
| + | |||
| + | ====Ba-133==== | ||
| + | |||
| + | [[File:Ba-133_ecapture.png | 600 px]] | ||
| + | |||
| + | Ba-133 undergoes electron capture to Cs-133. 86% of the time it ends up in the 1/2+ , 437 keV excited state of Cs-133. The 437 state emmits a 356 keV photon as it transitions to the 81 keV state on its way to the ground state. We see photons of energy 81 keV and 356 keV in coincidence as the lifetime in the 81 keV state is so short. | ||
| + | |||
| + | {| border="1" |cellpadding="20" cellspacing="0 | ||
| + | |- | ||
| + | | Energy(keV) || Intensity(rel) | ||
| + | |- | ||
| + | | 53.1625( 6) ||2.199(22) | ||
| + | |- | ||
| + | | 79.6139(13) || 2.62( 6) | ||
| + | |- | ||
| + | | '''80.9971(12)''' || 34.06(27) | ||
| + | |- | ||
| + | | 160.6109(17) || 0.645( 8) | ||
| + | |- | ||
| + | | 223.2373(14) || 0.450( 4) | ||
| + | |- | ||
| + | | 276.3997(13) || 7.164(22) | ||
| + | |- | ||
| + | | 302.8510( 6) || 18.33( 6) | ||
| + | |- | ||
| + | | ''' 356.0134( 6)''' || 62.05(19) | ||
| + | |- | ||
| + | | 383.8480(12) || 8.94( 3) | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | The 81 keV and 356 keV lines are the strongest and, when they occur in coincidence, they represent the transition from the 436 keV excited state of Cs-133 to the 81 keV excited state and then the ground state. | ||
| + | |||
| + | If I put a cut on the strongest line (356 keV) observed by Det B and ask what photon energies are observed in coincidence (timing window of 53 ns) with the other HpGe detector (Detector 180-2) I see the spectrum | ||
| + | |||
| + | |||
| + | [[File:R5716_356CoinOverlay.png | 400 px]] | ||
| + | |||
| + | ==== Y-88==== | ||
| + | |||
| + | |||
| + | {| border="1" |cellpadding="20" cellspacing="0 | ||
| + | |- | ||
| + | | Energy (keV) || Relative Intensity | ||
| + | |- | ||
| + | | 850.6 || 0.065 | ||
| + | |- | ||
| + | |'''898.042''' || 93.7 | ||
| + | |- | ||
| + | | 1382.2 || 0.021 | ||
| + | |- | ||
| + | | '''1836.063 ''' || 99.2 | ||
| + | |- | ||
| + | | 2734.0 || 0.71 | ||
| + | |- | ||
| + | | 3219.7 || 0.0070 | ||
| + | |} | ||
Latest revision as of 01:52, 3 November 2014
Abstract
ISU's intermediate energy nuclear physics group is presently involved in several fundamental physics measurements. This talk will describe a program to measure the fractional polarization of down quarks in a nucleon using polarized electrons to probe polarized nucleon targets. Quantum chromodynamcs (QCD) is a theory of the strong interaction; one of the four fundamental forces in nature. QCD predicts that the down quark will carry all of the nucleon's spin and result in a fractional polarization of unity when the probe interacts with down quarks that carry all of the nucleon's momentum. This theory contradicts the leading constituent quark model of the nucleon. The world's current data set is unable to discriminate between QCD's prediction and the constituent quark model. A description of this experimental program and the roles of ISU graduate students will be described.
electron scattering (collisions)
Elastic Collisions: Conserve P and E
Inelastic : Only Conserve P
Four Momentum
Using Ryder 4-momentum tensor convention:
If I take the inner product of a particles four momentum with itself I get
The Energy-Momentum relation
The and are the reciprocal quantities to and
For a plane wave
Similarly
The de Broglie relation
if its a massless particle (photon) then
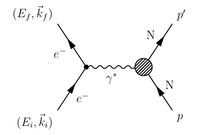
Definition of Momentum Transfer
- Conservation of Momentum
- Momentum Transfer
- Momentum Transfer Squared
- A space-like scattering event
Space-like interval: Two events are separated by a space like interval then there isn't enough time passing between them to allow a cause-effect relationship because a photon can't traverse the distance. This means that there is no reference frame that may be used to describe the event as happening at the same spatial location but there is a frame that describes them happening at the same time. If the spacetime interval between the two events is defined as s then for a space-like interval
Time-like interval: Two events are separated by a time like interval if enough time passes between them to allow a cause-effect relationship. This means that there is no reference frame that may be used to describe the event as happening at the same time but there is one that describes them happening at the same spatial location. If the spacetime interval between the two events is defined as s then for a time-like interval
4-Momentum vector definition using Ryder convention
- if you define the speed of light as unity
- Note
- Other conventions used by Perkins
or Kollen
Momentum transfer is defined as
- : conservation of momentum
Definition of Missing Mass
Inelastic scattering (Energy is not conserved but absorbed from the momentum transfer)
- 4-momentum conservation
- Invariant Missing Mass = mass of the intermediate state that was created.
Get picture from Figure 1.3 on pg 13 to show how cross section changes with Q^2
http://arxiv.org/pdf/0812.2144.pdf
F1 for several Q^2 to show how it smooths out
http://www.jlab.org/Hall-B/secure/eg1/Models/InclusiveModels.html
DIS scattering theory
http://www.physics.umd.edu/courses/Phys741/xji/chapter4.pdf
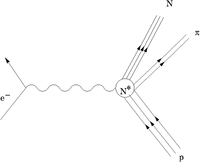
The Delta Resonance
Decay Modes:
- Vector current of the virtual photon exchange
Spin 1/2 and 3/2 final states
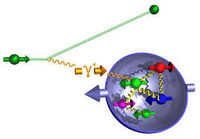
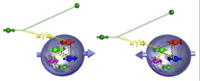
Double Spin Asymmetry
If both the target and the incident virtual photon are polarized then one can measure the cross-section for two separate conditions; when the spins are parallel and anti-parallel.
Let
- photon helicity is anti-parallel to the target spin
- photon helicity is parallel to the target spin.
 |
|
|---|---|
| (Struck quark spin is to Nucleon spin) | (Struck quark spin is to Nucleon spin) |
Clebsch Gordan recoupling
The recoupling of two subsystems with angular momenta and to a new system with total angular momentum is written as
= expansion of the systems total angular momentum in terms of the uncoupled original basis states of each individual constituent
: all other possible m_1 and m_2 values don't add to M
: all other possible m_1 and m_2 values don't add to M
If I constrain the helicity of my virtual photon to be +1 by preparing electrons with spins along their direction of motion, then the state doesn't exist so only only one state enters the sum
: all other possible m_1 and m_2 values don't add to M
: Clebsch-Gordon Coefficient
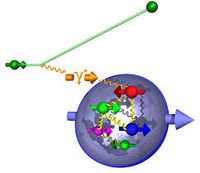
Quark Distributions
The polarized distributions may be expressed in a similar fashion:
 |

|
|---|---|
| (Struck quark spin is to Nucleon spin) | (Struck quark spin is to Nucleon spin) |
Duality
where
is the maximum (minimum) value of x for the interval of W being considered
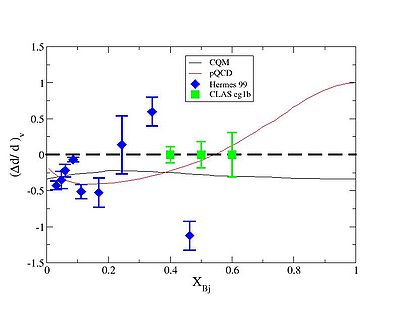
Polarized QUark distributions
Delta d-over d
Past student pojects
GEM fission chamber
U-233 source inside GEM detector with cathode voltage = 3585 and GEM voltage = 2870
CPAA
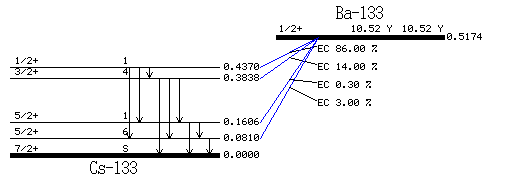
Ba-133
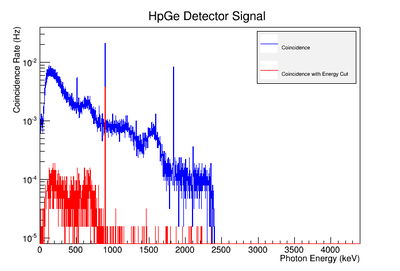
Ba-133 undergoes electron capture to Cs-133. 86% of the time it ends up in the 1/2+ , 437 keV excited state of Cs-133. The 437 state emmits a 356 keV photon as it transitions to the 81 keV state on its way to the ground state. We see photons of energy 81 keV and 356 keV in coincidence as the lifetime in the 81 keV state is so short.
| Energy(keV) | Intensity(rel) |
| 53.1625( 6) | 2.199(22) |
| 79.6139(13) | 2.62( 6) |
| 80.9971(12) | 34.06(27) |
| 160.6109(17) | 0.645( 8) |
| 223.2373(14) | 0.450( 4) |
| 276.3997(13) | 7.164(22) |
| 302.8510( 6) | 18.33( 6) |
| 356.0134( 6) | 62.05(19) |
| 383.8480(12) | 8.94( 3) |
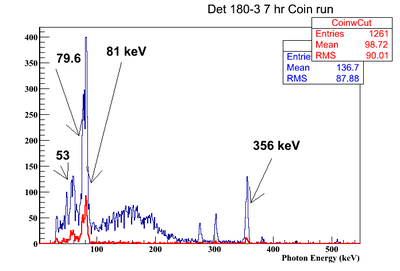
The 81 keV and 356 keV lines are the strongest and, when they occur in coincidence, they represent the transition from the 436 keV excited state of Cs-133 to the 81 keV excited state and then the ground state.
If I put a cut on the strongest line (356 keV) observed by Det B and ask what photon energies are observed in coincidence (timing window of 53 ns) with the other HpGe detector (Detector 180-2) I see the spectrum
Y-88
| Energy (keV) | Relative Intensity |
| 850.6 | 0.065 |
| 898.042 | 93.7 |
| 1382.2 | 0.021 |
| 1836.063 | 99.2 |
| 2734.0 | 0.71 |
| 3219.7 | 0.0070 |
References
Past colloquia
Theory
Phenomenological
NP, B291(1987)793; NP, B346(1990)1;
Z. Phys. C56(1992)493;
Eur. Phys. J. C44 (2005)219;
hep-ph/0205123
arXiV:1310.5285
QCD inspired
NP, B483(1997)291; NP, B484(1997)265;
PRL 85(2000)3591; PRL 89(2002)162301;
JHEP 0211(2002)44; NP, A720(2003)131;
Eur. Phys. J. C30(2003)213; arXiV:09073534;
NP, A761(2005)67; PR, C81(2010)024902
Hybrids
PYTHIA + BUU simulation
PR, C70(2004)054609; NP, A801(2008)68
Experiment
keith's 2012 talk in Italy on EG1-DVCS
Unpolarized
http://link.springer.com/article/10.1007%2FJHEP04%282014%29005
File:AndyMiller 200TalkAtDESY.pdf 2002 talk by CA Miller at DESY
File:Dueren.98.055.pdf 1998 Duren talk
July 30,2014 talk by XingLong Li at Heremes File:XingLongLi TalkOnPACIAEmdoelForSIDIS.pdf from
Xiangs proposal for CLAS12 measurement of SIDIS Xsections see Fig. 1
Semi-inclusive deep inelastic scattering at small transverse momentum
Naomi's SIDIS Hermes talk from 2011 at NNPSS11