Difference between revisions of "Forest UCM Ch3 Rockets"
| (15 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | =Rocket problem 1= | |
| − | [[File:Forest_UCM_Ch3_Rockets_Fig.png]][[File:Forest_UCM_Ch3_Rockets_Fig.xfig.txt]] | + | Remember the hobo problem? This is how rockets are propelled by expending fuel (mass). |
| + | |||
| + | Lets first think about the inverse rocket where mass is added instead of expelled. | ||
| + | |||
| + | Consider a railroad car with frictionless wheels moving at speed <math>v</math> on level ground. | ||
| + | |||
| + | A hobo handing from a tree drops down onto the railroad car as it is moving under the tree. | ||
| + | |||
| + | What is the final velocity of a railroad car after the hobo jumps on. | ||
| + | |||
| + | ;Conservation of momentum | ||
| + | |||
| + | :<math>Mv = (M+m) v_f</math> | ||
| + | |||
| + | :<math>v_f = \frac{M}{M+m} v</math> | ||
| + | |||
| + | The railroad car slows down after the hobo jumps on. | ||
| + | |||
| + | Rockets work in a similar fashion. They speed up after the fuel "jumps" off. | ||
| + | |||
| + | =Rocket Problem 2= | ||
| + | Consider a rocket of mass <math>m</math> moving at a speed <math>v</math> ejecting rocket fuel for propulsion. | ||
| + | |||
| + | |||
| + | [[File:Forest_UCM_Ch3_Rockets_Fig.png | 400 px]][[File:Forest_UCM_Ch3_Rockets_Fig.xfig.txt]] | ||
<math>m =</math> mass of Fuel + Rocket | <math>m =</math> mass of Fuel + Rocket | ||
| − | <math> | + | <math>-dm =</math> mass of Fuel ejected over time interval <math>dt</math> ( <math>dm</math> = mass lost by rocket < 0) |
| + | |||
| + | <math>u =v_{FR}</math> velocity of Fuel relative to the Rocket | ||
| + | |||
| + | <math>v =</math> velocity of rocket relative to the ground before ejecting fuel of mass <math>(-dm)</math> | ||
| + | |||
| + | <math>v+dv =v_{RG}</math> velocity of the rocket relative to the ground after ejecting fuel | ||
| + | |||
| + | <math>V_FG =</math> Velocity of the fuel with respect to the ground | ||
| + | |||
| + | = Apply Conservation of Momentum= | ||
| + | :<math>mv = (-dm)V_{FG} + (m-(-dm))(v+dv)</math> | ||
| + | :<math>dmV_{FG} = mdv + dm (v+dv)</math> | ||
| + | |||
| + | The velocity of the fuel with respect to the ground<math> (V_{FG})</math> may be written as the vector sum of the rocket's velocity with respect to the ground <math>(V_{RG})</math> and the velocity of the fuel with respect to the rocket <math>(V_{FR})</math> :Galilean transormation | ||
| + | |||
| + | :<math>\vec{V}_{FG} - \vec{V}_{FR} + \vec{V}_{RG}</math> | ||
| + | |||
| + | assuming 1-D motion and using the velocity variables defined above | ||
| + | |||
| + | :<math>V_{FG} = -u + (v+dv)</math> | ||
| + | |||
| + | substituting | ||
| + | |||
| + | :<math>dm \left (-u + (v+dv) \right ) = mdv + dm (v+dv)</math> | ||
| + | :<math>-udm = mdv </math> | ||
| + | |||
| + | ==solving for the velocity== | ||
| + | |||
| + | : <math>\int_{v_0}^v = \int_{m_0}^m -u \frac{dm}{m}</math> | ||
| + | : <math>v - v_0 = u \ln \left (\frac{m_0}{m} \right )</math> | ||
| + | : <math>v = v_0 + u \ln \left (\frac{m_0}{m} \right )</math> | ||
| + | |||
| + | where <math>m_0</math> is the initial Rocket mass | ||
| + | |||
| + | ==In terms of Thrust== | ||
| + | |||
| + | Defining | ||
| + | :<math>\mbox{THRUST} = - \dot{m} u</math> | ||
| + | Then | ||
| + | :<math>m \dot{v} =</math> THRUST = Force on rocket as a result of expelling fuel | ||
[[Forest_UCM_MnAM#Rockets]] | [[Forest_UCM_MnAM#Rockets]] | ||
Latest revision as of 13:59, 13 September 2014
Rocket problem 1
Remember the hobo problem? This is how rockets are propelled by expending fuel (mass).
Lets first think about the inverse rocket where mass is added instead of expelled.
Consider a railroad car with frictionless wheels moving at speed on level ground.
A hobo handing from a tree drops down onto the railroad car as it is moving under the tree.
What is the final velocity of a railroad car after the hobo jumps on.
- Conservation of momentum
The railroad car slows down after the hobo jumps on.
Rockets work in a similar fashion. They speed up after the fuel "jumps" off.
Rocket Problem 2
Consider a rocket of mass moving at a speed ejecting rocket fuel for propulsion.
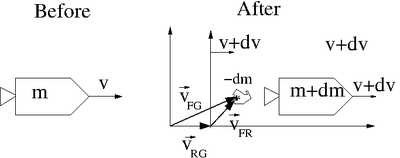 File:Forest UCM Ch3 Rockets Fig.xfig.txt
File:Forest UCM Ch3 Rockets Fig.xfig.txt
mass of Fuel + Rocket
mass of Fuel ejected over time interval ( = mass lost by rocket < 0)
velocity of Fuel relative to the Rocket
velocity of rocket relative to the ground before ejecting fuel of mass
velocity of the rocket relative to the ground after ejecting fuel
Velocity of the fuel with respect to the ground
Apply Conservation of Momentum
The velocity of the fuel with respect to the ground may be written as the vector sum of the rocket's velocity with respect to the ground and the velocity of the fuel with respect to the rocket :Galilean transormation
assuming 1-D motion and using the velocity variables defined above
substituting
solving for the velocity
where is the initial Rocket mass
In terms of Thrust
Defining
Then
- THRUST = Force on rocket as a result of expelling fuel