Forest Bhabha Scattering

Bhabha (electron -positron) Scattering

Bhabha scattering identifies the scatterng of an electron and positron (particle and anti-particle). There are two processes that can occur

1.) scattering via the "instantaneous" exchange of a virtual photon

2.) annihilation in which the e+ and e- spend some time as a photon which then reconverts back to an e+e- pair

Step 1 Draw the Feynman Diagram

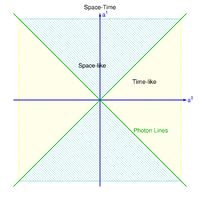
The Feynman diagram is a space-time description of the interaction where the horizontal axis (abscissa) is used to denote time and the vertical axis (ordinate) is 3-D space.

A particle which travels only along the horizontal time axis is not moving in space while a particle traveling only along the vertical axis is not moving in time (within the uncertainty principle).

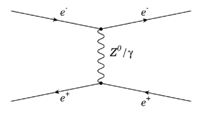
e+e- scattering (t-channel) (space-like)

If the electron and positron simply scatter off of one another via a coulomb interaction, then they exchange a photon along the space axis. You start with an external line from the left to represent the electron. This is a "t-channel" process in which one of the particles emits a virtual photon that is absorbed by the other particle. You can tell the exchanged particle is virtual if it is drawn parallel to the time axis in the Feynman diagram.

The time axis is from left to right so the Virtual particle is along the space axis (in some books the diagram has the space axis horizontal). Also note that a virtual, neutral Z-boson may also be exchanged via the electro-weak interaction.

Momentum conservation at the electron vertex

[math]p^{\mu}_{in}(e^-) = p^{\mu}_{out}(\gamma^*) + p^{\mu}_{out}(e^-) [/math]

[math]\Rightarrow p^{\mu}_{out}(\gamma^*) = p^{\mu}_{in}(e^-) - p^{\mu}_{out}(e^-) [/math]

[math] q^{\mu} = (E_{\gamma},\vec{p_{\gamma}})= (E_1,\vec{p1}) - (E_2,\vec{p_2}) = (E_1-E_2,\vec{p1} - \vec{p_2})[/math]

[math]q^2 = q_{\mu}q^{\mu}= (E_1-E_2,-(\vec{p1} - \vec{p_2})) (E_1-E_2,\vec{p1} - \vec{p_2})= (E_1-E_2)^2-(\vec{p1} - \vec{p_2}) \cdot (\vec{p1} - \vec{p_2})[/math]

[math] = (E_1-E_2)^2-p_1^2 -p_2^2 + 2p_1p_2 \cos(\theta)[/math]

[math] = (E_1^2 - p_1^2 +E_2^2 - p_2^2 - 2E_1E_2+ 2p_1p_2 \cos(\theta)[/math]

[math]E_{\gamma}^2 - p_{\gamma}^2= m_1^2 + m_2^2 -4p_1p_2\sin^2(\theta/2)[/math]

for the case that the electron and positron have equal and opposite momentum (CM frame) the exchanged particle is clearly a virtual photon

[math] p^{\mu}_{out}(\gamma^*) = (2m_e,\vec{0})[/math]

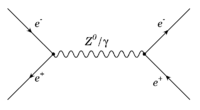
e+e- Annihilation (s-channel) (time-like)

If the electron and positron form an intermediate state which then decays back to an electron and positron. This is a "s-channel" process in which

Momentum conservation at the first vertex

[math]p^{\mu}_{in}(e^-)= p^{\mu}_{in}(e^+) + p^{\mu}_{out}(\gamma^*) [/math] In reality the

Step 2 identify 4-Momentum conservation

Let:

[math]p_1 \equiv[/math] initial electron 4-momentum

[math]u_1 \equiv[/math] initial electron spinor

[math]p_2 \equiv[/math] final electron 4-momentum

[math]u_2 \equiv[/math] final electron spinor

[math]p_3 \equiv[/math] initial positron 4-momentum

[math]\bar{u}_3 \equiv[/math] initial positron spinor

[math]p_4 \equiv[/math] finial positron 4-momentum

[math]\bar{u}_4 \equiv[/math] finial positron spinor

Matrix element for scattering

According to the Feynman RUles for QED:

the term

[math]ig_e \gamma^{\mu}[/math]

is used at the vertex to describe the Quantum electrodynamic (electromagneticc) interaction between the two fermion spinor states entering the vertex and forming a photon which will "connect" this vertex with the next one.

The QED interaction Lagrangian is

[math]-eA_{\mu} \bar{\Psi} \gamma^{\mu} \Psi[/math]

[math]\mathcal{M}_s = \,[/math] [math]e^2 \left( \bar{u}_{3} \gamma^\nu u_4 \right) \frac{1}{(p_1+p_2)^2} \left( \bar{u}_{2} \gamma_\nu u_{1} \right) [/math]

Matrix element for annihilation

[math]\mathcal{M}_a = \,[/math] [math]-e^2 \left( \bar{u}_{3} \gamma^\mu u_{1} \right) \frac{1}{(p_1-p_3)^2} \left( \bar{u}_{2} \gamma_\mu u_4 \right) [/math]

Radiative Bhabha Scattering to measure running of alpha

http://arxiv.org/pdf/hep-ex/0105065.pdf

Forest_QMII