Forest Bhabha Scattering

Bhabha (electron -positron) Scattering

Bhabha scattering identifies the scatterng of an electron and positron (particle and anti-particle). There are two processes that can occur

1.) scattering via the exchange of a virtual photon

2.) annihilation in which the e+ and e- spend some time as a photon which then reconverts back to an e+e- pair

Step 1 Draw the Feynman Diagram

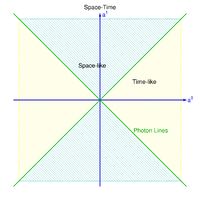
The Feynman diagram is a space-time description of the interaction where the horizontal axis (abscissa) is used to denote time and the vertical axis (ordinate) is 3-D space.

A particle which travels only along the horizontal time axis is not moving in space while a particle traveling only along the vertical axis is not moving in time (within the uncertainty principle).

e+e- scattering

If the electron and positron simply scatter off of one another via a coulomb interaction, then they exchange a virtual photon along the space axis. You start with an external line from the left to represent the electron

Step 2 identify 4-Momentum conservation

Let:

[math]p_1 \equiv[/math] initial electron 4-momentum

[math]u_1 \equiv[/math] initial electron spinor

[math]p_2 \equiv[/math] final electron 4-momentum

[math]u_2 \equiv[/math] final electron spinor

[math]:p_3 \equiv[/math] initial positron 4-momentum

[math]\bar{u}_3 \equiv[/math] initial positron spinor

[math]p_4 \equiv[/math] finial positron 4-momentum

[math]\bar{u}_4 \equiv[/math] finial positron spinor

Matrix element for scattering

According to the Feynman RUles for QED:

the term

[math]ig_e \gamma^{\mu}[/math]

is used at the vertex to describe the Quantum electrodynamic (electromagneticc) interaction between the two fermion spinor states entering the vertex and forming a photon which will "connect" this vertex with the next one.

The QED interaction Lagrangian is

[math]-eA_{\mu} \bar{\Psi} \gamma^{\mu} \Psi[/math]

[math]\mathcal{M}_s = \,[/math] [math]e^2 \left( \bar{u}_{3} \gamma^\nu u_4 \right) \frac{1}{(p_1+p_2)^2} \left( \bar{u}_{2} \gamma_\nu u_{1} \right) [/math]

Matrix element for annihilation

[math]\mathcal{M}_a = \,[/math] [math]-e^2 \left( \bar{u}_{3} \gamma^\mu u_{1} \right) \frac{1}{(p_1-p_3)^2} \left( \bar{u}_{2} \gamma_\mu u_4 \right) [/math]

Forest_QMII