Difference between revisions of "Forest Error Analysis for the Physical Sciences"
| Line 340: | Line 340: | ||
==A ROOT Primer== | ==A ROOT Primer== | ||
| + | ===Download=== | ||
| + | |||
| + | You can usually download the ROOT software for multiple platforms for free at the URL below | ||
| + | |||
| + | [http://root.cern.ch] | ||
| + | |||
| + | ===Setup the environment=== | ||
==plotting Probability Distributions in ROOT== | ==plotting Probability Distributions in ROOT== | ||
Revision as of 16:37, 13 January 2012
Class Admin
Forest_ErrorAnalysis_Syllabus
Homework
Homework is due at the beginning of class on the assigned day. If you have a documented excuse for your absence, then you will have 24 hours to hand in the homework after being released by your doctor.
Class Policies
http://wiki.iac.isu.edu/index.php/Forest_Class_Policies
Instructional Objectives
- Course Catalog Description
- Error Analysis for the Physics Sciences 3 credits. Lecture course with computation requirements. Topics include: Error propagation, Probability Distributions, Least Squares fit, multiple regression, goodness of fit, covariance and correlations.
Prequisites:Math 360.
- Course Description
- The application of statistical inference and hypothesis testing will be the main focus of this course for students who are senior level undergraduates or beginning graduate students. The course begins by introducing the basic skills of error analysis and then proceeds to describe fundamental methods comparing measurements and models. A freely available data analysis package known as ROOT will be used. Some programming skills will be needed using C/C++ but a limited amount of experience is assumed.
Objectives and Outcomes
Forest_ErrorAnalysis_ObjectivesnOutcomes
Suggested Text
Data Reduction and Error Analysis for the Physical Sciences by Philip Bevington ISBN: 0079112439
Systematic and Random Uncertainties
Although the name of the class is "Error Analysis" for historical purposes, a more accurate description would be "Uncertainty Analysis". "Error" usually means a mistake is made while "Uncertainty" is a measure of how confident you are in a measurement.
Accuracy -vs- Precision
- Accuracy
- How close does an experiment come to the correct result
- Precision
- a measure of how exactly the result is determine. No reference is made to what the result means.
Systematic Error
What is a systematic error?
A class of errors which result in reproducible mistakes due to equipment bias or a bias related to its use by the observer.
Example:
1.) A ruler
a.) A ruler could be shorter or longer because of temperature fluctuations
b.) An observer could be viewing the markings at a glancing angle.
In this case a systematic error is more of a mistake than an uncertainty.
In some cases you can correct for the systematic error. In the above Ruler example you can measure how the ruler's length changes with temperature. You can then correct this systematic error by measuring the temperature of the ruler during the distance measurement.
Correction Example:
A ruler is calibrated at 25 C an has an expansion coefficient of (0.0005 0.0001 m/C.
You measure the length of a wire at 20 C and find that on average it is m long.
This means that the 1 m ruler is really (1-(20-25 C)(0.0005 m/C)) = 0.99775
So the correction becomes
1.982 *( 0.99775) =1.977 m
- Note
- The numbers above without decimal points are integers. Integers have infinite precision. We will discuss the propagation of the errors above in a different chapter.
Error from bad technique:
After repeating the experiment several times the observer discovers that he had a tendency to read the meter stick at an angle and not from directly above. After investigating this misread with repeated measurements the observer estimates that on average he will misread the meter stick by 2 mm. This is now a systematic error that is estimated using random statistics.
Reporting Uncertainties
Notation
X Y = X(Y)
Significant Figures and Round off
Significant figures
- Most Significant digit
- The leftmost non-zero digit is the most significant digit of a reported value
- Least Significant digit
- The least significant digit is identified using the following criteria
- 1.) If there is no decimal point, then the rightmost digit is the least significant digit.
- 2.)If there is a decimal point, then the rightmost digit is the least significant digit, even if it is a zero.
In other words, zero counts as a least significant digit only if it is after the decimal point. So when you report a measurement with a zero in such a position you had better mean it.
- The number of significant digits in a measurement are the number of digits which appear between the least and most significant digits.
examples:
| Measurement | most Sig. digit | least Sig. | Num. Sig. Dig. | Scientific Notation |
| 5 | 5 | 5 | 1* | |
| 5.0 | 5 | 0 | 2 | |
| 50 | 5 | 0 | 2* | |
| 50.1 | 5 | 1 | 3 | |
| 0.005001 | 5 | 1 | 4 |
- Note
- The values of "5" and "50" above are ambiguous unless we use scientific notation in which case we know if the zero is significant or not.
Round Off
Measurements that are reported which are based on the calculation of more than one measured quantity must have the same number of significant digits as the quantity with the smallest number of significant digits.
To accomplish this you will need to round of the final measured value that is reported.
To round off a number you:
1.) Increment the least significant digit by one if the digit below it (in significance) is greater than 5.
2.) Do nothing if the digit below it (in significance) is less than 5.
Then truncate the remaining digits below the least significant digit.
- What happens if the next significant digit below the least significant digit is exactly 5?
To avoid a systematic error involving round off you would ideally randomly decide to just truncate or increment. If your calculation is not on a computer with a random number generator, or you don't have one handy, then the typical technique is to increment the least significant digit if it is odd (or even) and truncate it if it is even (or odd).
- Examples
The table below has three entries; the final value calculated from several measured quantities, the number of significant digits for the measurement with the smallest number of significant digits, and the rounded off value properly reported using scientific notation.
| Value | Sig. digits | Rounded off value |
| 12.34 | 3 | |
| 12.36 | 3 | |
| 12.35 | 3 | |
| 12.35 | 2 |
Statistics abuse
http://www.worldcat.org/oclc/28507867
http://www.worldcat.org/oclc/53814054
Statistical Distributions
Propagation of Uncertainties
Statistical inference
Final Exam
The Final exam will be to write a report describing the analysis of the data in TF_ErrAna_InClassLab#Lab_16
Grading Scheme:
Grid Search method results
10% Parameter values
20% Parameter errors
30% Probability fit is correct
40% Grammatically correct written explanation of the data analysis with publication quality plots
Report and source code due in my office by Thursday May 6, 2:30 pm (MST)
Report length is between 3 and 15 pages all inclusive.
Hypothesis testing distributions
Chi-squared
t-Distribution
The Student's t-distribution is defined as
t-distribution is a "one tailed" test typically used for small sample sizes (N > 24) where the parent population mean is known.
F-distribution
For this class we shall define a hypothesis test as a test used to
There are two schools of thought on this
Chi-Square
comparing experiment with theory/function
Comparing 2 experiments
P-value
Root fundtion to evaluate meaning of Chi-square
PDG => Rather, the p-value is
the probability, under the assumption of a hypothesis H , of obtaining data at least as
incompatible with H as the data actually observed.
From http://en.wikipedia.org/wiki/P-value and http://en.wikipedia.org/wiki/Statistical_significance
the p-value is the frequency or probability with which the observed event would occur, if the null hypothesis were true. If the obtained p-value is smaller than the significance level, then the null hypothesis is rejected.
In some fields, for example nuclear and particle physics, it is common to express statistical significance in units of "σ" (sigma), the standard deviation of a Gaussian distribution. A statistical significance of "" can be converted into a value of α via use of the error function:
The use of σ is motivated by the ubiquitous emergence of the Gaussian distribution in measurement uncertainties. For example, if a theory predicts a parameter to have a value of, say, 100, and one measures the parameter to be 109 ± 3, then one might report the measurement as a "3σ deviation" from the theoretical prediction. In terms of α, this statement is equivalent to saying that "assuming the theory is true, the likelihood of obtaining the experimental result by coincidence is 0.27%" (since 1 − erf(3/√2) = 0.0027).
What is a p-value?
A p-value is a measure of how much evidence we have against the null hypothesis. The null hypothesis, traditionally represented by the symbol H0, represents the hypothesis of no change or no effect.
The smaller the p-value, the more evidence we have against H0. It is also a measure of how likely we are to get a certain sample result or a result “more extreme,” assuming H0 is true. The type of hypothesis (right tailed, left tailed or two tailed) will determine what “more extreme” means.
Much research involves making a hypothesis and then collecting data to test that hypothesis. In particular, researchers will set up a null hypothesis, a hypothesis that presumes no change or no effect of a treatment. Then these researchers will collect data and measure the consistency of this data with the null hypothesis.
The p-value measures consistency by calculating the probability of observing the results from your sample of data or a sample with results more extreme, assuming the null hypothesis is true. The smaller the p-value, the greater the inconsistency.
Traditionally, researchers will reject a hypothesis if the p-value is less than 0.05. Sometimes, though, researchers will use a stricter cut-off (e.g., 0.01) or a more liberal cut-off (e.g., 0.10). The general rule is that a small p-value is evidence against the null hypothesis while a large p-value means little or no evidence against the null hypothesis. Please note that little or no evidence against the null hypothesis is not the same as a lot of evidence for the null hypothesis.
It is easiest to understand the p-value in a data set that is already at an extreme. Suppose that a drug company alleges that only 50% of all patients who take a certain drug will have an adverse event of some kind. You believe that the adverse event rate is much higher. In a sample of 12 patients, all twelve have an adverse event.
The data supports your belief because it is inconsistent with the assumption of a 50% adverse event rate. It would be like flipping a coin 12 times and getting heads each time.
The p-value, the probability of getting a sample result of 12 adverse events in 12 patients assuming that the adverse event rate is 50%, is a measure of this inconsistency. The p-value, 0.000244, is small enough that we would reject the hypothesis that the adverse event rate was only 50%.
A large p-value should not automatically be construed as evidence in support of the null hypothesis. Perhaps the failure to reject the null hypothesis was caused by an inadequate sample size. When you see a large p-value in a research study, you should also look for one of two things:
a power calculation that confirms that the sample size in that study was adequate for detecting a clinically relevant difference; and/or a confidence interval that lies entirely within the range of clinical indifference. You should also be cautious about a small p-value, but for different reasons. In some situations, the sample size is so large that even differences that are trivial from a medical perspective can still achieve statistical significance.
As a statistician, I am not in a good position to advise you on whether a difference is trivial or not. As a medical expert, you need to balance the cost and side effects of a treatment against the benefits that the therapy provides.
The authors of the research paper should inform you what size difference is clinically relevant and what sized difference is trivial. But if they don't, you should. Ask yourself how much of a difference would be large enough to cause you to change your practice. Then compare this to the confidence interval in the research paper. If both limits of the confidence interval are smaller than a clinically relevant difference, then you should not change your practice, no matter what the p-value tells you.
You should not interpret the p-value as the probability that the null hypothesis is true. Such an interpretation is problematic because a hypothesis is not a random event that can have a probability.
Bayesian statistics provides an alternative framework that allows you to assign probabilities to hypotheses and to modify these probabilities on the basis of the data that you collect.
Example
A large number of p-values appear in a publication
Consultation Patterns and Provision of Contraception in General Practice Before Teenage Pregnancy: Case-Control Study. Churchill D, Allen J, Pringle M, Hippisley-Cox J, Ebdon D, Macpherson M, Bradley S. British Medical Journal 2000: 321(7259); 486-9. [Abstract] [Full text] [PDF]
by Churchill et al 2000. This was a study of consultation practices among teenagers who become pregnant. The researchers selected 240 patients (cases) with a recorded conception before the age of 20. Three controls were selected for each case and were matched on age and practice.
The not too surprising finding is that the cases were more likely to have consulted certain health professionals in the year before conception and were more likely to request contraceptive protection. This demonstrates that teenagers are not reluctant to seek advice about contraception.
For example, 91% of the cases (219/240) sought the advice of a general practitioner in the year before conception compared to 82% of the controls (586/719) during a similar time frame. This is a large difference. The odds ratio is 2.37. The p-value is 0.001, which indicates that this ratio is statistically significantly different from 1.0. The 95% confidence interval for the odds ratio is 1.45 to 3.86.
In contrast, 23% of the cases (56/240) sought advice from a practice nurse while 24% of the controls (170/719) sought advice. This is a small difference and the odds ratio is 0.98. The p-value is 0.905, which indicates that this odds ratio does not differ significantly from 1. As with any negative finding, you should be concerned about whether the result is due to an inadequate sample size. The confidence interval, however, is 0.69 to 1.39. This indicates that the research study had a good amount of precision and that the sample size was reasonable.
root [3] TMath::Prob(1.31,11) Double_t Prob(Double_t chi2, Int_t ndf) Computation of the probability for a certain Chi-squared (chi2) and number of degrees of freedom (ndf). Calculations are based on the incomplete gamma function P(a,x), where a=ndf/2 and x=chi2/2. P(a,x) represents the probability that the observed Chi-squared for a correct model should be less than the value chi2. The returned probability corresponds to 1-P(a,x), which denotes the probability that an observed Chi-squared exceeds the value chi2 by chance, even for a correct model.
--- NvE 14-nov-1998 UU-SAP Utrecht
t-test
Komolgorov test
http://en.wikipedia.org/wiki/Kolmogorov-Smirnov_test
Homework
References
1.) "Data Reduction and Error Analysis for the Physical Sciences", Philip R. Bevington, ISBN-10: 0079112439, ISBN-13: 9780079112439
CPP programs for Bevington
2.)An Introduction to Error Analysis, John R. Taylor ISBN 978-0-935702-75-0
3.) ROOT: An Analysis Framework
4.) Orear, "Notes on Statistics for Physicists"
5.) Statistical Methods for Engineers and Scientists, Robert M. Bethea, Benjamin S. Duran, and Thomas L. Boullion, Marcel Dekker Inc, New York, (1985), QA 276.B425
6.) Data Analysis for Scientists and Engineers, Stuart L. Meyer, John Wiley & Sons Inc, New York, (1975), QA 276.M437
ROOT comands
A ROOT Primer
Download
You can usually download the ROOT software for multiple platforms for free at the URL below
Setup the environment
plotting Probability Distributions in ROOT
http://project-mathlibs.web.cern.ch/project-mathlibs/sw/html/group__PdfFunc.html
The Binomial distribution is plotted below for the case of flipping a coin 60 times (n=60,p=1/2)
- You can see the integral , Mean and , RMS by right clicking on the Statistics box and choosing "SetOptStat". A menu box pops up and you enter the binary code "1001111" (without the quotes).
root [0] Int_t i;
root [1] Double_t x
root [2] TH1F *B30=new TH1F("B30","B30",100,0,100)
root [3] for(i=0;i<100;i++) {x=ROOT::Math::binomial_pdf(i,0.5,60);B30->Fill(i,x);}
root [4] B30->Draw();
You can continue creating plots of the various distributions with the commands
root [2] TH1F *P30=new TH1F("P30","P30",100,0,100)
root [3] for(i=0;i<100;i++) {x=ROOT::Math::poisson_pdf(i,30);P30->Fill(i,x);}
root [4] P30->Draw("same");
root [2] TH1F *G30=new TH1F("G30","G30",100,0,100)
root [3] for(i=0;i<100;i++) {x=ROOT::Math::gaussian_pdf(i,3.8729,30);G30->Fill(i,x);}
root [4] G30->Draw("same");
The above commands created the plot below.
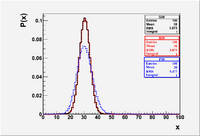 File:Forest EA BinPosGaus Mean30.eps
File:Forest EA BinPosGaus Mean30.eps
- Note
- I set each distribution to correspond to a mean () of 30. The of the Binomial distribution is = 60(1/2)(1/2) = 15. The of the Poisson distribution is defined to equal the mean . I intentionally set the mean and sigma of the Gaussian to agree with the Binomial. As you can see the Binomial and Gaussian lay on top of each other while the Poisson is wider. The Gaussian will lay on top of the Poisson if you change its to 5.477
for(i=0;i<100;i++) {x=ROOT::Math::gaussian_pdf(i,5.477,30);G30->Fill(i,x);}
- Also Note
- The Gaussian distribution can be used to represent the Binomial and Poisson distributions when the average is large ( ie:). The Poisson distribution, though, is an approximation to the Binomial distribution for the special case where the average number of successes is small ( because )
Int_t i;
Double_t x
TH1F *B30=new TH1F("B30","B30",100,0,10);
TH1F *P30=new TH1F("P30","P30",100,0,10);
for(i=0;i<10;i++) {x=ROOT::Math::binomial_pdf(i,0.1,10);B30->Fill(i,x);}
for(i=0;i<10;i++) {x=ROOT::Math::poisson_pdf(i,1);P30->Fill(i,x);}
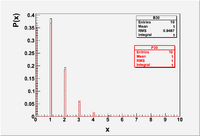 File:Forest EA BinPos Mean1.eps
File:Forest EA BinPos Mean1.eps
Other probability distribution functions
double beta_pdf(double x, double a, double b) double binomial_pdf(unsigned int k, double p, unsigned int n) double breitwigner_pdf(double x, double gamma, double x0 = 0) double cauchy_pdf(double x, double b = 1, double x0 = 0) double chisquared_pdf(double x, double r, double x0 = 0) double exponential_pdf(double x, double lambda, double x0 = 0) double fdistribution_pdf(double x, double n, double m, double x0 = 0) double gamma_pdf(double x, double alpha, double theta, double x0 = 0) double gaussian_pdf(double x, double sigma = 1, double x0 = 0) double landau_pdf(double x, double s = 1, double x0 = 0.) double lognormal_pdf(double x, double m, double s, double x0 = 0) double normal_pdf(double x, double sigma = 1, double x0 = 0) double poisson_pdf(unsigned int n, double mu) double tdistribution_pdf(double x, double r, double x0 = 0) double uniform_pdf(double x, double a, double b, double x0 = 0)
Sampling from Prob Dist in ROOT
You can also use ROOT to generate random numbers according to a given probability distribution.
In the example generates 1000 random numbers from a Poisson Parent population with a mean of 10
root [0] TRandom r
root [1] TH1F *P10=new TH1F("P10","P10",100,0,100)
root [2] for(i=0;i<10000;i++) P10->Fill(r.Poisson(30));
Warning: Automatic variable i is allocated (tmpfile):1:
root [3] P10->Draw();
Other possibilities
Gaussian with a mean of 30 and sigma of 5
root [1] TH1F *G10=new TH1F("G10","G10",100,0,100)
root [2] for(i=0;i<10000;i++) G10->Fill(r.Gauss(30,5)); //mean of 30 and sigma of 5
root [3] G10->Draw("same");
There is also
G10->Fill(r.Uniform(20,50)); // Generates a uniform distribution between 20 and 50
G10->Fill(r.Exp(30)); // exponential distribution with a mean of 30
G10->Fill(r.Landau(30,5)); // Landau distribution with a mean of 30 and sigma of 5
G10->Fill(r.BreitWigner(30,5)); mean of 30 and gamma of 5