Difference between revisions of "Neutron Polarimeter"
| Line 89: | Line 89: | ||
<math>\delta t = 1\ ns</math> | <math>\delta t = 1\ ns</math> | ||
| − | The neutron kinetic energy is: | + | The neutron kinetic energy as function of time of flight is: |
<math>T_n = m_n (\gamma - 1) = m_n\left[ \frac{1}{\sqrt{1-\left(\frac{l}{c\ t}\right)^2}} - 1 \right]</math> | <math>T_n = m_n (\gamma - 1) = m_n\left[ \frac{1}{\sqrt{1-\left(\frac{l}{c\ t}\right)^2}} - 1 \right]</math> | ||
| Line 105: | Line 105: | ||
| − | Say, | + | Say, the detector is 1.5 m away and neutron's time of flight uncertainty is: |
| + | <math>\delta t = 1\ ns</math> | ||
| − | [[File:Error table01.png | | + | |
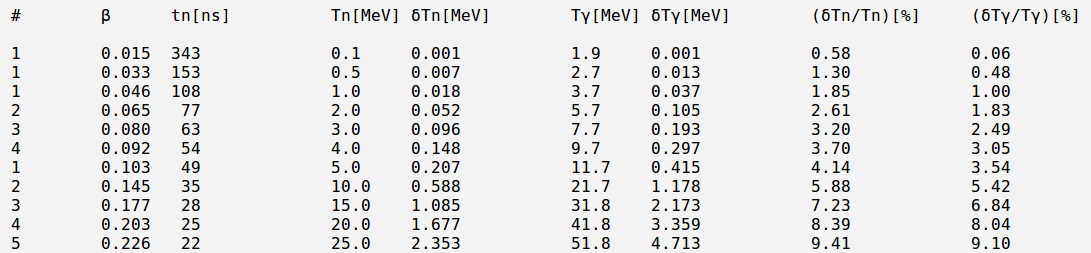
| + | In the table below presented some calculation results using the formulas above: | ||
| + | |||
| + | |||
| + | [[File:Error table01.png | 1100 px]] | ||
Revision as of 05:41, 6 April 2011
Four-vector Algebra
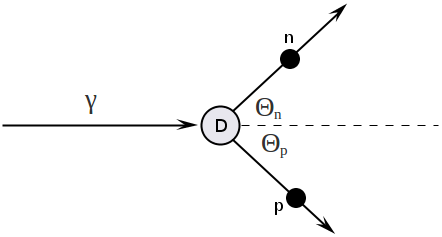
Consider two bode reaction :
Write down four-momentum vectors before and after reaction:
Now apply the law of conservation of four-momentum vectors:
Squaring both side of equation above and using the four-momentum invariants we have:
Detector located at case
Detector is located at , and the formula above is simplified:
We can easily solve the equation above with respect to incident photon energy:
For non-relativistic neutrons and the formula above is become:
Substituting the corresponding masses, we get finally:
and visa versa:
Here I derived the formula [2] just inversing the formula [1]. I can as well start from exact solution above, solve this equation with respect to neutron energy, do the non-relativistic approximation and get exactly the same formula [2]. But anyway we ended up with two useful non-relativistic formulas we can analyze now:
1) from formula [1] above we can predict the threshold of reaction in direction:
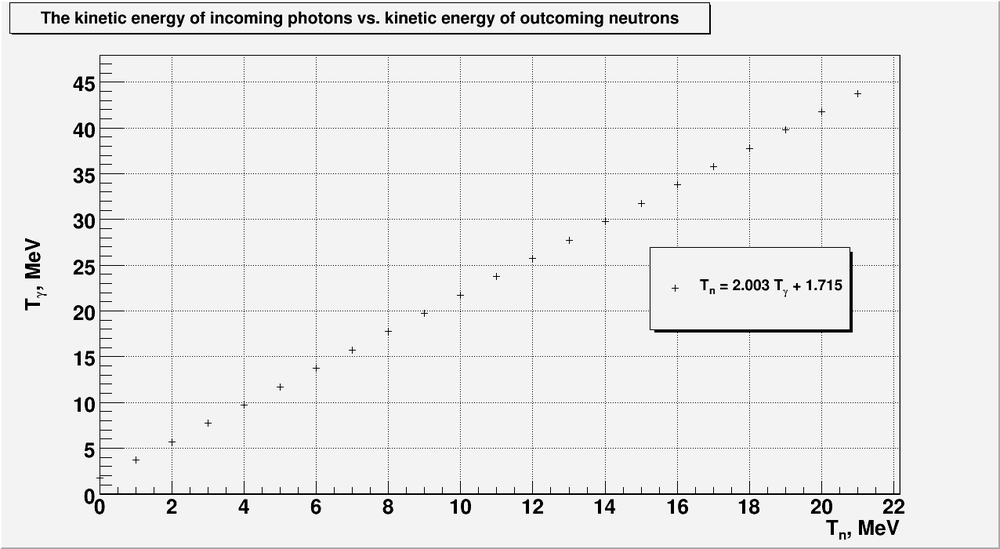
2) from formula [1] above we can predict the incident photon energy based on the detected neutron energy (neutron polarimeter).
3) from formula [2] above we can predict the detected neutron energy based on the incident photon energy.
- for the incident photons up to we can detect neutrons up to
- for the incident photons up to we can detect neutrons up to
4) we can do the error calculations.
Example of error calculation
example 1
Say, we have, 10 MeV neutron with uncertainty 1 MeV, the corresponding uncertainly for photons energy is:
example 2
In the calculations below I attempted to predict the uncertainty in photons energy based on uncertainly of neutrons time of flight.
Say, the neutron's time of flight uncertainty is:
The neutron kinetic energy as function of time of flight is:
By taking derivative of the expression above we can find the relative neutron energy error:
Also we need to know the neutron time of flight as function of the neutron energy:
Say, the detector is 1.5 m away and neutron's time of flight uncertainty is:
In the table below presented some calculation results using the formulas above: